因子分析及R使用
目录
什么是因子分析
因子分析与主成分分析区别
因子的特点
R语言实现
极大似然法
主成分法因子分析
因子旋转法
因子得分计算
因子排名与做图
因子信息重叠图
例2
什么是因子分析
因子分析-factor analysis,就是寻找这些公共因子的模型分析方法,它是在主成分的基础上构筑若干意义较为明确的公因子,以他们为框架分解原变量,以此考察原变量间的联系与区别。因子分析就是从大量的数据中“由表及里”、“去粗取精”,寻找影响或支配变量的多变量统计方法。
因子分析的主要用途在于:
(1)减少分析变量个数
(2)通过对变量间相关关系的探测,将原始变量进行分类,即将相关性高的变量分为一组,用共性因子代替该组变量。
因子分析与主成分分析区别
就统计上而言,主成分分析所侧重的是如何转换原始变量使之成为一些综合性的新指标,其关键在于“变异数”的问题,与主成分分析不同的是,因子分析重视的是如何解决变量之间的“共变异数”问题,因为每一反应变量均为一些“公共因子变量”和”特殊性变量“的线性函数,其中“共同因子变量”可以反应变量间的共变量,而特殊性变量部分则只对其所属的变量之变异数有所贡献,所以主成分分析是“变异数”导向的方法,因子分析则是“共变异数”导向的方法。
因子分析也是数据缩减的一种多变量分析方法,它是基于信息损失最小化而提出的一种非常有效的方法。它把众多的指标综合成为减少的几个公共指标,这些指标即是因子,
因子的特点
(1)因子变量的数量远远少于原始变量个数
(2)因子变量并非原始变量的简单取舍,而是新的综合
(3)因子变量之间没有线性关系
(4)因子变量具有明确解释性,可最大限度的发挥专业分析的作用。
R语言实现
观测数据较多,所以指标之间不可避免存在多重共线性问题,因此有必要先计算观测数据的相关矩阵
x1 x2 x3 x4 x5 x6
冀东水泥 33.8 34.75 0.67 59.77 15.49 16.35
大同水泥 27.54 28.04 2.36 35.29 -20.96 -46.45
四川双马 22.86 23.47 0.61 42.83 5.48 -49.22
牡丹江 19.05 19.95 1 48.51 -12.32 -65.99
西水股份 20.84 21.17 1.08 48.45 65.09 54.81
狮头股份 28.14 28.84 2.51 24.52 -6.43 -15.94
太行股份 30.45 31.13 1.02 46.14 6.57 -16.59
海螺水泥 36.29 36.96 0.27 58.31 70.85 117.59
尖峰集团 16.94 17.26 0.61 52.04 9.03 -94.05
四川金顶 28.74 29.4 0.6 65.46 -33.97 -55.02
祁连山 33.31 34.3 1.17 45.8 12.18 39.46
华新水泥 25.08 26.12 0.64 69.35 22.38 -10.2
福建水泥 34.51 35.44 0.38 61.61 23.91 -163.99
天鹅股份 25.52 26.73 1.1 47.02 -4.51 -68.79
复制数据,运行代码
> X=read.table("clipboard",header=T)#读取例9.1数据
> cor(X)
x1 x2 x3 x4 x5 x6
x1 1.00000000 0.9991983 -0.09974689 0.18850763 0.2010041 0.29778271
x2 0.99919830 1.0000000 -0.10420434 0.19672979 0.1903570 0.28747808
x3 -0.09974689 -0.1042043 1.00000000 -0.83715637 -0.4087603 0.01518741
x4 0.18850763 0.1967298 -0.83715637 1.00000000 0.2585103 -0.02928244
x5 0.20100410 0.1903570 -0.40876032 0.25851029 1.0000000 0.58029333
x6 0.29778271 0.2874781 0.01518741 -0.02928244 0.5802933 1.00000000
>
极大似然法
x1与x2高度正相关,x3与x4较强复相关,x5与x6呈中度相关。为消除各财务指标之间的相关性,采用因子分析法提取因子。
下面为极大似然法提取公因子:
> (FA0=factanal(X,3,rot="none"))#极大似然法因子分析
Call:
factanal(x = X, factors = 3, rotation = "none")
Uniquenesses:
x1 x2 x3 x4 x5 x6
0.005 0.005 0.005 0.271 0.005 0.548
Loadings:
Factor1 Factor2 Factor3
x1 0.950 -0.307
x2 0.948 -0.310
x3 -0.340 -0.782 0.517
x4 0.363 0.561 -0.531
x5 0.454 0.693 0.556
x6 0.383 0.163 0.527
Factor1 Factor2 Factor3
SS loadings 2.402 1.623 1.140
Proportion Var 0.400 0.271 0.190
Cumulative Var 0.400 0.671 0.861
The degrees of freedom for the model is 0 and the fit was 1.1422
>
由此可见,前三个因子所解释的方差占整个方差的86%以上,基本可以全面反映六项财务指标的信息,即是Cumulative Var的值。所以我们提取前三个因子作为公共因子,但各因子的经济含义不明显,还需进行进一步分析,即因子旋转法
主成分法因子分析
> library(mvstats)
载入程辑包:‘mvstats’
The following object is masked _by_ ‘.GlobalEnv’:
H.clust
> (Fac=factpc(X,3))#主成份法因子分析
$`Vars`
Vars Vars.Prop Vars.Cum
Factor1 2.570 0.4283 42.83
Factor2 1.713 0.2855 71.38
Factor3 1.249 0.2082 92.19
$loadings
Factor1 Factor2 Factor3
x1 0.7829 0.5029 -0.3624
x2 0.7811 0.4964 -0.3756
x3 -0.5786 0.7685 0.0802
x4 0.5951 -0.6990 -0.2415
x5 0.6317 -0.1457 0.6557
x6 0.5084 0.3367 0.6943
$scores
Factor1 Factor2 Factor3
冀东水泥 1.10805 0.19287 -0.40233
大同水泥 -1.07195 1.46385 -0.37413
四川双马 -0.58577 -0.49848 0.24193
牡丹江 -1.17442 -0.77791 0.08986
西水股份 -0.05264 -0.46073 2.31615
狮头股份 -1.05007 2.04151 0.25174
太行股份 0.20807 0.48809 -0.23430
海螺水泥 2.20745 0.32524 1.16336
尖峰集团 -1.11541 -1.53235 0.39013
四川金顶 0.09714 -0.60602 -1.45691
祁连山 0.66096 1.03293 0.04173
华新水泥 0.41359 -1.08331 0.19805
福建水泥 0.86840 -0.53255 -1.82104
天鹅股份 -0.51340 -0.05315 -0.40422
$Rank
F Ri
冀东水泥 0.48359 3
大同水泥 -0.12910 8
四川双马 -0.37184 11
牡丹江 -0.76615 13
西水股份 0.35587 4
狮头股份 0.20127 5
太行股份 0.19490 6
海螺水泥 1.38882 1
尖峰集团 -0.90457 14
四川金顶 -0.47152 12
祁连山 0.63632 2
华新水泥 -0.09863 7
福建水泥 -0.17273 9
天鹅股份 -0.34622 10
$common
x1 x2 x3 x4 x5 x6
0.9971 0.9976 0.9318 0.9011 0.8502 0.8539
> 主因子法比极大似然估计发提取效果好一些92.19%,因极大似然法要求数据来自多元正态分布,这一点一般很难满足。
因子旋转法
建立因子模型,处理找出主因子,还要知道主因子的意义,如果因子代表的变量不是很突出,还需进行旋转,正交旋转和斜交旋转是因子旋转的两类方法,最常用的是最大方差正交旋转法-Varimax
> (Fa1=factanal(X,3,rot="varimax")) #varimax法旋转因子分析
Call:
factanal(x = X, factors = 3, rotation = "varimax")
Uniquenesses:
x1 x2 x3 x4 x5 x6
0.005 0.005 0.005 0.271 0.005 0.548
Loadings:
Factor1 Factor2 Factor3
x1 0.983 0.155
x2 0.985 0.142
x3 -0.990 -0.124
x4 0.127 0.844
x5 0.293 0.953
x6 0.210 0.631
Factor1 Factor2 Factor3
SS loadings 1.998 1.800 1.367
Proportion Var 0.333 0.300 0.228
Cumulative Var 0.333 0.633 0.861
The degrees of freedom for the model is 0 and the fit was 1.1422
Loadings代表旋转后的因子载荷,可以看出旋转后的经济意义十分明显,F1在主营业务利润率x1上的载荷大道0.983,在销售毛利率x2上的载荷达到0.985,因此,因子F1代表企业的盈利能力,反应企业的投资收益情况,是资金周转营运能力的结果,也是资金流动偿债能力的基础。因子F2代表了企业的偿债能力,类似的,因子F3在主营业务收入增长率x5和营业利润率x6上的载荷值分别是0.953和0.631,所以因子F3代表了企业的发展能力,反应企业持续经营发展能力的指标。
因子得分计算
因子模型建立后,还有一个重要的作用是应用因子分析模型去评价每个样本在整个模型中的地位,即是进行综合评价,例如,地区经济发展的因子分析模型建立后,我们希望知道每个地区经济发展的情况,吧区域经济划分归类,那些地区发展较快,那些较慢,那些不快不慢等,这时需要将公共因子用变量的线性组合来表示,也即有地区经济的各项指标值来估计它的因子得分。
就冀东水泥来说,他的盈利能力建好,偿贷能力一般,发展能力中的偏下。
> Fa1=factanal(X,3,scores="regression")#使用回归估计法的极大似然法因子分析
> Fa1$scores
Factor1 Factor2 Factor3
冀东水泥 1.0571 0.49858 -0.01932
大同水泥 0.2508 -1.97182 -0.55062
四川双马 -0.7619 0.61936 -0.35643
牡丹江 -1.2622 0.10831 -0.82490
西水股份 -1.4124 -0.36520 2.09840
狮头股份 0.2993 -2.28407 0.06540
太行股份 0.5368 -0.01725 -0.16548
海螺水泥 1.1383 0.86089 1.85549
尖峰集团 -1.7990 0.62143 -0.20236
四川金顶 0.4397 0.83905 -1.87521
祁连山 1.0220 -0.27756 0.10237
华新水泥 -0.4381 0.53317 0.26013
福建水泥 1.1144 0.91988 0.13561
天鹅股份 -0.1847 -0.08479 -0.52308
>
> Fac1=factpc(X,3,scores="regression")#使用回归估计法的主成份法因子分析
> Fac1$scores
Factor1 Factor2 Factor3
冀东水泥 1.10805 0.19287 -0.40233
大同水泥 -1.07195 1.46385 -0.37413
四川双马 -0.58577 -0.49848 0.24193
牡丹江 -1.17442 -0.77791 0.08986
西水股份 -0.05264 -0.46073 2.31615
狮头股份 -1.05007 2.04151 0.25174
太行股份 0.20807 0.48809 -0.23430
海螺水泥 2.20745 0.32524 1.16336
尖峰集团 -1.11541 -1.53235 0.39013
四川金顶 0.09714 -0.60602 -1.45691
祁连山 0.66096 1.03293 0.04173
华新水泥 0.41359 -1.08331 0.19805
福建水泥 0.86840 -0.53255 -1.82104
天鹅股份 -0.51340 -0.05315 -0.40422
> 因子排名与做图
下面是因子1的排名与做图,应力能力最高的就是海螺水泥,福建水泥,冀东水泥,祁连山
> factanal.rank(Fa1,plot=T) #排名与做图
$`Fs`
Factor1 Factor2 Factor3
冀东水泥 1.0570974 0.49858291 -0.01931786
大同水泥 0.2508467 -1.97181549 -0.55061886
四川双马 -0.7618827 0.61936154 -0.35643016
牡丹江 -1.2621905 0.10831340 -0.82489689
西水股份 -1.4124102 -0.36519764 2.09839517
狮头股份 0.2992651 -2.28406622 0.06540023
太行股份 0.5367516 -0.01725097 -0.16547708
海螺水泥 1.1383136 0.86088890 1.85548532
尖峰集团 -1.7990483 0.62142573 -0.20235665
四川金顶 0.4396610 0.83905494 -1.87521145
祁连山 1.0220466 -0.27756182 0.10236965
华新水泥 -0.4381137 0.53317006 0.26012980
福建水泥 1.1143517 0.91988289 0.13560911
天鹅股份 -0.1846884 -0.08478822 -0.52308034
$Ri
F rank
冀东水泥 0.57762286 3
大同水泥 -0.73582797 14
四川双马 -0.17323177 9
牡丹江 -0.66885707 13
西水股份 -0.11845569 8
狮头股份 -0.66290875 12
太行股份 0.15786371 5
海螺水泥 1.23140339 1
尖峰集团 -0.53300988 11
四川金顶 -0.03369328 7
祁连山 0.32577583 4
华新水泥 0.08514207 6
福建水泥 0.78759236 2
天鹅股份 -0.23941579 10
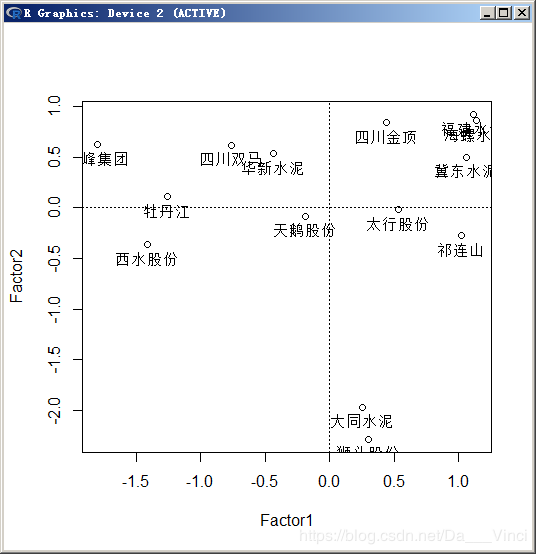
> 在因子得分图中,综合排名靠前的在第一象限,排名靠后的大多在第四象限,总得来说,各企业间的差距非常明显,而且三种能力都好的企业很少,因此在水泥发展方面,各上市公司应该经常兼顾三种经营能力的协调发展,锐意改革,提供公司的业绩。
因子信息重叠图
biplot(Fa1$scores,Fa1$loadings)#前2个因子信息重叠图 例2
X1 X2 X3 X4 X5 X6 X7 X8
北京 4934.05 1512.88 981.13 1294.07 2328.51 2383.96 1246.19 649.66
天津 4249.31 1024.15 760.56 1163.98 1309.94 1639.83 1417.45 463.64
河北 2789.85 975.94 546.75 833.51 1010.51 895.06 917.19 266.16
山西 2600.37 1064.61 477.74 640.22 1027.99 1054.05 991.77 245.07
内蒙古 2824.89 1396.86 561.71 719.13 1123.82 1245.09 941.79 468.17
辽宁 3560.21 1017.65 439.28 879.08 1033.36 1052.94 1047.04 400.16
吉林 2842.68 1127.09 407.35 854.8 873.88 997.75 1062.46 394.29
黑龙江 2633.18 1021.45 355.67 729.55 746.03 938.21 784.51 310.67
上海 6125.45 1330.05 959.49 857.11 3153.72 2653.67 1412.1 763.8
江苏 3928.71 990.03 707.31 689.37 1303.02 1699.26 1020.09 377.37
浙江 4892.58 1406.2 666.02 859.06 2473.4 2158.32 1168.08 467.52
安徽 3384.38 906.47 465.68 554.44 891.38 1169.99 850.24 309.3
福建 4296.22 940.72 645.4 502.41 1606.9 1426.34 1261.18 375.98
江西 3192.61 915.09 587.4 385.91 732.97 973.38 728.76 294.6
山东 3180.64 1238.34 661.03 708.58 1333.63 1191.18 1027.58 325.64
河南 2707.44 1053.13 549.14 626.55 858.33 936.55 795.39 300.19
湖北 3455.98 1046.62 550.16 525.32 903.02 1120.29 856.97 242.82
湖南 3243.88 1017.59 603.18 668.53 986.89 1285.24 869.59 315.82
广东 5056.68 814.57 853.18 752.52 2966.08 1994.86 1444.91 454.09
广西 3398.09 656.69 491.03 542.07 932.87 1050.04 803.04 277.43
海南 3546.67 452.85 519.99 503.78 1401.89 837.83 819.02 210.85
重庆 3674.28 1171.15 706.77 749.51 1118.79 1237.35 968.45 264.01
四川 3580.14 949.74 562.02 511.78 1074.91 1031.81 690.27 291.32
贵州 3122.46 910.3 463.56 354.52 895.04 1035.96 718.65 258.21
云南 3562.33 859.65 280.62 631.7 1034.71 705.51 673.07 174.23
西藏 3836.51 880.1 271.29 272.81 866.33 441.02 628.35 335.66
陕西 3063.69 910.29 513.08 678.38 866.76 1230.74 831.27 332.84
甘肃 2824.42 939.89 505.16 564.25 861.47 1058.66 768.28 353.65
青海 2803.45 898.54 484.71 613.24 785.27 953.87 641.93 331.38
宁夏 2760.74 994.47 480.84 645.98 859.04 863.36 910.68 302.17
新疆 2760.69 1183.69 475.23 598.78 890.3 896.79 736.99 331.8
> X=read.table("clipboard",header=T)#读取例7.2数据
> library(mvstats)
> Fac0=factpc(X,3)#因子分析
> Fac0$Vars#方差及贡献率
Vars Vars.Prop Vars.Cum
Factor1 5.7012 0.71265 71.26
Factor2 1.0287 0.12858 84.12
Factor3 0.5043 0.06304 90.43
> 公因子F1几乎占据了所有重要指标,F2的x2相对较大,这两个因子即可代表该城市的发达程度和消费水平。
> Fac1=factpc(X,3,rot="varimax")#运用旋转因子分析
Factor Analysis for Princomp in Varimax:
> Fac1$Vars#方差及贡献率
Vars Vars.Prop Vars.Cum
Factor1 4.016 50.20 50.20
Factor2 1.680 21.00 71.20
Factor3 1.538 19.22 90.43
> Fac0$loadings#因子载荷
Factor1 Factor2 Factor3
X1 0.8429 -0.43524 0.12432
X2 0.5956 0.68671 0.37005
X3 0.8926 -0.09008 -0.05094
X4 0.7202 0.47829 -0.44596
X5 0.8979 -0.32885 0.08740
X6 0.9647 -0.07045 0.06403
X7 0.8858 -0.05691 -0.31385
X8 0.8939 0.12018 0.20046
> Fac1$loadings#因子载荷
Factor1 Factor2 Factor3
X1 0.9463 0.1159 0.08084
X2 0.1527 0.2499 0.93676
X3 0.7580 0.4145 0.24728
X4 0.2249 0.8743 0.36250
X5 0.9231 0.2125 0.15722
X6 0.8252 0.3638 0.35547
X7 0.6864 0.6337 0.11656
X8 0.6843 0.2980 0.54462> Fac1$scores#因子得分
Factor1 Factor2 Factor3
北京 1.18092 1.74118 2.0290303
天津 0.20460 2.96179 -0.7387309
河北 -0.92649 1.20877 -0.4632058
山西 -0.78973 0.43269 -0.0522166
内蒙古 -0.62006 -0.18964 2.1005492
辽宁 -0.51315 1.07679 -0.1140626
吉林 -1.04765 1.15843 0.4542682
黑龙江 -1.16020 0.29219 0.2627968
上海 3.25451 -0.50217 1.4096665
江苏 0.60518 0.14247 -0.2101378
浙江 1.38897 -0.19508 1.4370242
安徽 -0.15415 -0.44702 -0.3504643
福建 1.14760 -0.30179 -0.7812963
江西 -0.08324 -1.25789 -0.1147615
山东 -0.26270 0.28871 0.7222037
河南 -0.75769 -0.09266 0.3236384
湖北 -0.18783 -0.59587 0.0211735
湖南 -0.24456 0.06551 0.0408756
广东 2.50339 0.69802 -1.7414243
广西 0.01884 -0.23030 -1.5152172
海南 0.43204 -0.14803 -2.7440469
重庆 -0.16768 0.43917 0.2490205
四川 0.05602 -1.08548 -0.0581755
贵州 -0.11095 -1.47558 -0.1667687
云南 -0.61547 -0.42528 -0.8159804
西藏 0.01200 -2.46313 -0.0009129
陕西 -0.42416 0.17032 -0.2713572
甘肃 -0.45628 -0.46636 0.0892125
青海 -0.66054 -0.42814 -0.0065357
宁夏 -0.78567 0.27927 -0.1067207
新疆 -0.83587 -0.65089 1.1125557
> Fac1$Rank#排名
F Ri
北京 1.49132 2
天津 0.64435 5
河北 -0.33214 18
山西 -0.34907 20
内蒙古 0.05826 10
辽宁 -0.05908 11
吉林 -0.21606 13
黑龙江 -0.52041 29
上海 1.98992 1
江苏 0.32440 7
浙江 1.03133 4
安徽 -0.26389 17
福建 0.40095 6
江西 -0.36273 21
山东 0.07473 8
河南 -0.37337 23
湖北 -0.23816 15
湖南 -0.11187 12
广东 1.18174 3
广西 -0.36514 22
海南 -0.37786 24
重庆 0.06183 9
四川 -0.23334 14
贵州 -0.43972 27
云南 -0.61393 31
西藏 -0.56553 30
陕西 -0.25362 16
甘肃 -0.34266 19
青海 -0.46754 28
宁夏 -0.39403 26
新疆 -0.37870 25
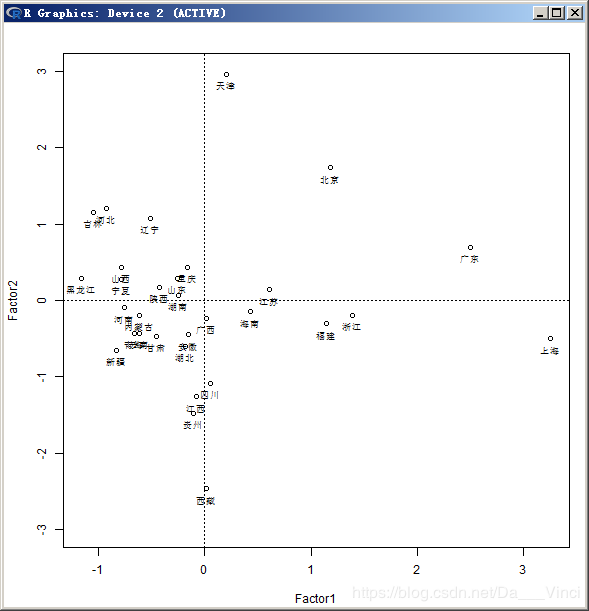
> par(mar=c(4,4,2,1)+0.1,cex=0.75) #
plot(Fac1$scores,ylim=c(-3,3)); abline(h = 0, v = 0, lty = 3)
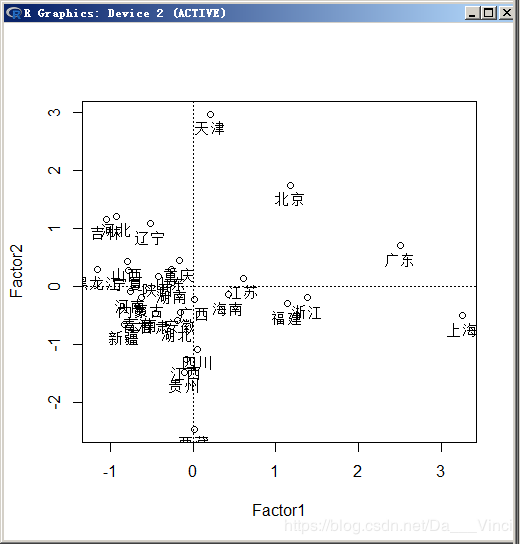
text(Fac1$scores,label=rownames(X),pos=1,adj=0.5,cex=0.8)
> plot.text(Fac1$scores) #因子得分图biplot(Fac1$scores,Fac1$loading) #信息重叠图