陆吾生讲座 最优化问题的数学基础

Ⅰ. Taylor expansion

对于光滑函数可以进行泰勒展开。
任意函数只要可以求导，放大看它的局部必是高阶的多项式求和的形式，根据要求的拟合误差决定需要的阶数。

One-variable case

f(x+δ)=f(x)+f′(x)δ+12f′′(x)δ2+…

Multi-variable case

def. Hessian Matrix: ∇2f(x)

f(x+δ)=f(x)+∇Tf(x)δ+12δT∇2f(x)δ+…

Linear approximation of f(x) at x

当 δ→0 ，f(x)是关于 δ 的线性函数

f(x+δ)≈f(x)+∇Tf(x)δ

Quadratic approximation of f(x) at x

当 δ→0 ，f(x)是关于 δ 的二次函数

f(x+δ)≈f(x)+∇Tf(x)δ+12δT∇2f(x)δ

---

Ⅱ. Optimazation

求 minx∈Rn×1f(x)

• 原始办法
  得到两个方程，但对于复杂函数而言求导后解方程极其复杂。
  

  ∇f(x)=⎡⎣⎢⎢⎢∂f(x)∂x1∂f(x)∂x2⎤⎦⎥⎥⎥=0

• A.Cauchy Method
  不通过解方程找到方程的解。
  随便找一个 xk ，然后使其移动得到更小的函数值，interatively，直到 ∇f(x)→0 .
  取 δ=−∇f(xk) ， xk+1=xk−∇f(xk)
  

  f(xk+δ)−f(xk)≈∇Tf(xk)δ=−||∇f(xk)2||<0
  故可以保证当前的 f(xk+δ) 比原先的 f(xk) 更小。
  以此为基础还可以设置步长 α
  
  F(α)=f(xk−α∇Tf(xk))
  得到的是关于 α 的非线性函数，当取到 αopt 时可以得到最小的函数值。
  
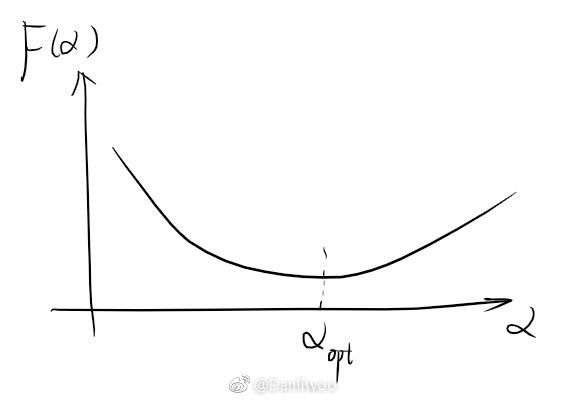
  关于 α 的选取，可参见Line search.
  以此迭代产生
  
  xk+1=xk−αk∇f(xk)
  xk+2=xk+1−αk+1∇f(xk+1)
  ...
  直到 ∇f(x)→0 .
  

• Newton Method
  上面的 α 求起来麻烦也不好估计。由于 f 同时也是关于 δ 的二阶多项式
  
  f(x+δ)≈f(x)+∇Tf(x)δ+12δT∇2f(x)δ
  故要求关于 δ 的最小值可关于 δ 求导
  
  ∇δ( f(xk)+∇Tf(xk)δ+12δT∇2f(xk)δ )=0
  且有性质
  ∇(cTx)=c
  可得到
  
  ∇f(xk)+∇2f(xk)δ=0
  则
  
  δ=−(∇2f(xk))−1∇f(xk)
  可以确定步长
  
  xk+1=xk−(∇2f(xk))−1∇f(xk)
  
  如图真实函数为黑线。一开始任取 xk ，其Taylor展开后对函数为红线的近似。求得红线的极值点为 xk+1 ，又得到绿色的近似，得到绿线的极值点为 xk+2 ，反复迭代不断地逼近理想的极值点。
  

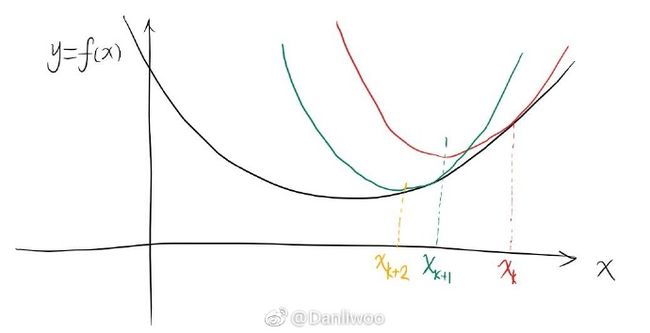
比较Cauchy和Newton的方法

比较哪种方法的质量好，可以通过 ∇f(x∗) ，越接近0的越好。同时收敛速度越快的也越好。

Method收敛速度预处理（求导等）占据内存Cauchy慢快小Newton快慢大

---

Ⅲ. Quadratic Form

Quadratic approximation of f(x) at x

f(x+δ)≈f(x)+∇Tf(x)δ+12δT∇2f(x)δ

中出现了Hessian Matrix H=∇2f(x) ，最后这项是一个二次型。

想知道二次型的正负性，取决于H的特征值 eig(H)−λ1,λ2,…,λn - real valued

def.⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪xTHx>0xTHx≥0xTHx<0xTHx≤0xTHx>,<0positive definite P.Dpositive semidefinite P.S.Dnegative definite N.Dnegative semidefinite N.S.Dindefiniteiffiffiffiffλi>0λi≥0λi<0λi≤0

比如

H=[12.52.54]

f(x)=xTHx=x21+5x1x2+4x22

det(λI−H)=[λ−12.52.5λ−4]=(λ−1)(λ−4)−6.25=0

陆老师一眼看出它是N.D，用了主子式(leading principal minors)简化运算：

1×4−6.25<0

妈妈我不懂……

Convex Function

对于开口向上的凸函数而言，其图像有性质：任何点的切线都在函数图象下方。

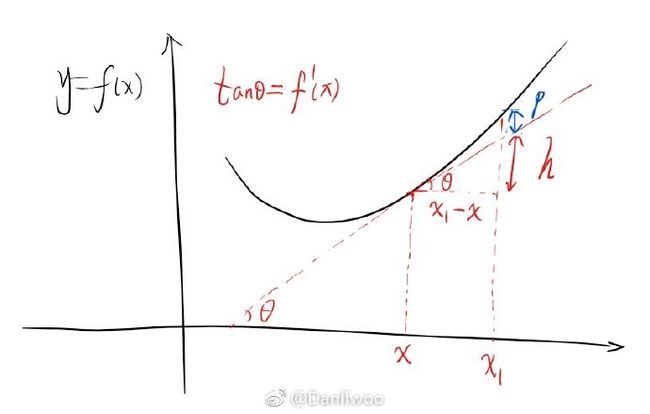
则对于x点处切线 tanθ=f′(x) ， θ 为切线与x轴夹角。且如图

h=tanθ(x1−x)=f′(x)(x1−x)

则

f(x1)=f(x)+h+p

又由Taylor展开项

f(x+δ)≈f(x)+∇Tf(x)δ+12δT∇2f(x)δ

代入到凸函数中得到

f(x1)≈f(x)+∇Tf(x)(x1−x)+12(x1−x)T∇2f(x)(x1−x)

则

f(x1)−f(x)−∇Tf(x)(x1−x)≈12(x1−x)T∇2f(x)(x1−x)≥0

即二次型是半正定的。
因此，求eig(H)则可得函数是否convex。

即使复杂如Logistic regression中的二阶梯度

∇2f(θ)=1N∑i=1N(1−2li)2e(1−2li)θTx^ix^ix^Ti(1+e(1−2li)θTx^i)2

也可判断出原函数为凸。

---

感谢陆老师~
ECNU的秋