从PCA和SVD的关系拾遗

从PCA和SVD的关系拾遗

---

最近突然看到一个问题，PCA和SVD有什么关系？隐约记得自己照猫画虎实现的时候PCA的时候明明用到了SVD啊，但SVD（奇异值分解）和PCA的（特征值分解）貌似差得相当远，由此钻下去搜集了一些资料，把我的一些收获总结一下，以免以后再忘记。

PCA的简单推导

PCA有两种通俗易懂的解释，1)是最大化投影后数据的方差(让数据更分散)；2)是最小化投影造成的损失。这两个思路最后都能推导出同样的结果。
下图应该是对PCA第二种解释展示得最好的一张图片了(ref:svd,pca,relation)

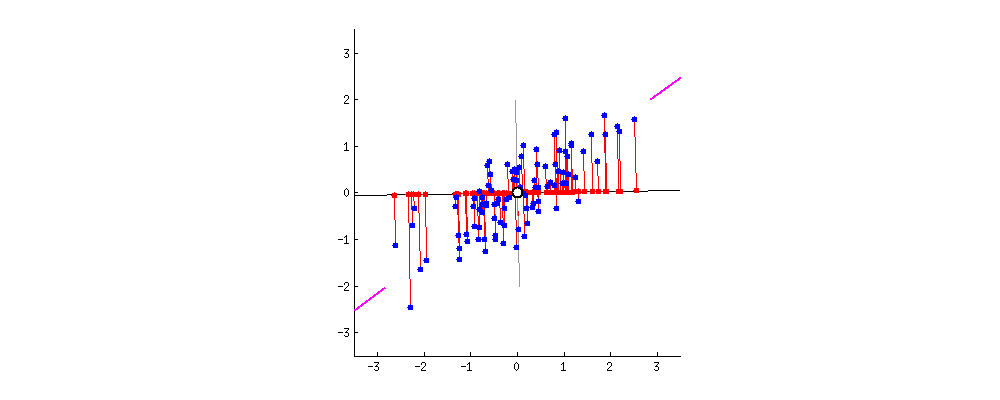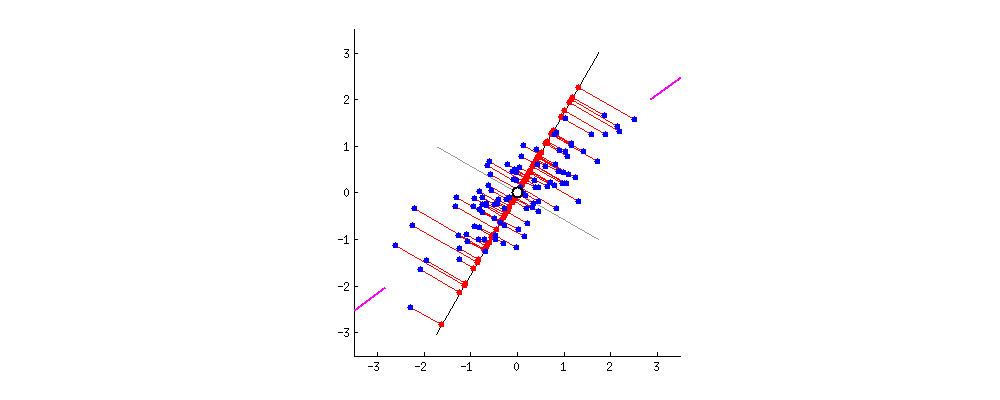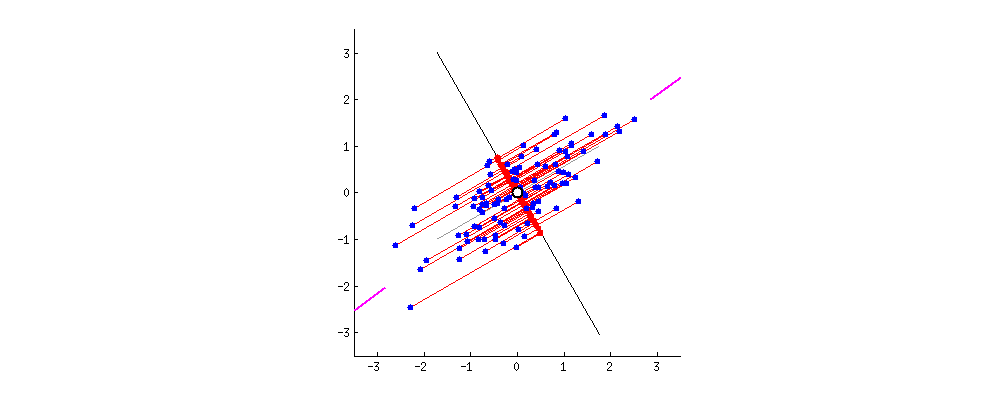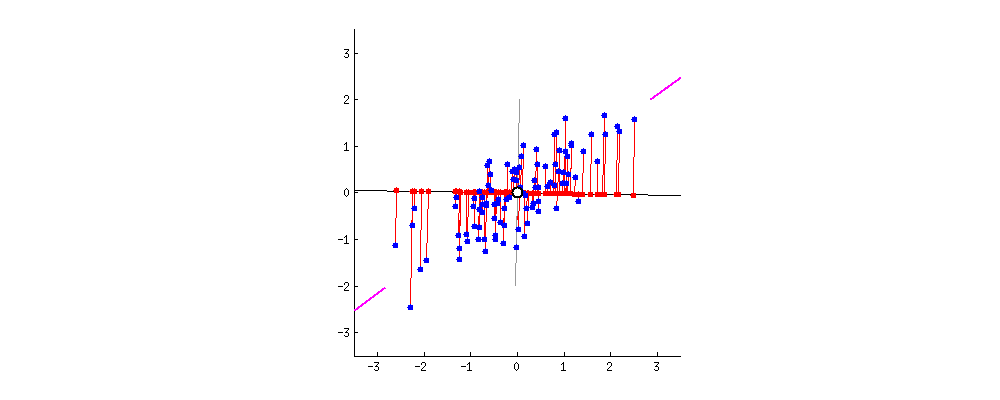
图示的数据都已经去中心化了（中心点为原点），这一步操作可以简单地通过 xi=xi−x¯ 来达到，其中 x¯ 是样本的均值，为方便表示，后文的 x 都是去中心化后的结果。
可以看到PCA所谓的降维操作就是找到一个新的坐标系（旋转的两条直线式垂直的，我们可以用一组标准正交基 {uj},j=1,...,n 来指示），然后减掉其中一些维度，使误差足够小。
假设我们要找的投影方向是 uj ( uj 是单位向量,即 uTjuj=1 ) ,点 xi 在该方向上的投影就是 (xTiuj)uj ，减掉这个维度造成的误差为：

Jj=1m∑i=1m(xTiuj)2=1m(xTuj)2=1m(xTuj)T(xTuj)=1muTjxxTuj

将 1mxxT 记作 S ，假设我们要减去t个维度，则需要最小化

J=∑j=n−tnuTjSujs.t.uTjuj=1

此时使用拉格朗日乘子法使得

J~=∑j=n−tnuTjSuj+λj(1−uTjuj)

最小化上式子，求导有

δJ~δuj=Suj−λjuj

使其为0则得到

Suj=λjuj

这是标准的特征值的定义， λj 就是特征值， uj 是对应的特征向量，所以对 S 进行特征值分解就可求得解， 将上式带回到原始的 J 中，可得

J=∑j=n−tnuTjSuj=∑j=n−tnuTjλjuj=∑j=n−tnλj

所以要使J最小，就去掉变换后维度中最小的t个特征值对应的维度就好了。
现在，我们再回过头看PCA的流程，就会发现一切都对应上了：

1. 对数据去中心化
2. 计算 XXT ，注:这里除或不除样本数量 M 或 M−1 其实对求出的特征向量没影响
3. 对 XXT 进行特征分解
4. 选取特征值最大的几个维度进行数据映射。（去掉较小的维度）

遗留问题

看到这有人要问了，我咋记得标准流程是计算矩阵的协方差矩阵呢？
我们来看协方差矩阵的计算公式：

Σ=E[(x−E[x])(x−E[x])⊤]

一开始我们的去中心化步骤其实就是计算了 (x−E[x]) ，然后 S=1mxxT 其实就是协方差矩阵，注意这里取的 1m ，实际操作中，应该是 1m−1 ，才是标准的协方差矩阵， 但这对最后找到的特征向量没有影响，对特征值之间的大小关系也没有影响。
所以到这一步标准的流程是（ 为了实现方便，下面代码中的矩阵 X 与其实是上面推导中的 XT ,每一行是一个样本，同时从这里开始的推导使用与代码一致的表示方法）：

def pca_01(X):
    covMat = np.cov(X,rowvar = 0)
    eigVal,eigVec = sp.linalg.eig(covMat)
    #do reduction with eigVal,eigVec

但因为最后用于变换的矩阵需要是去中心化后的，所以有些地方的实现是：

def pca_02(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    covMat = np.cov(X,rowvar = 0)#实际上是否去中心化对求到的协方差矩阵并无影响,只是方便后面进行降维
    eigVal,eigVec = sp.linalg.eig(covMat)
    #do reduction with eigVal,eigVec

使用矩阵乘法的方式：

def pca_03(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    M,N=X.shape
    Sigma=np.dot(X.transpose(),X)/(M-1)
    eigVal,eigVec = sp.linalg.eig(Sigma)
    #do reduction with eigVal,eigVec

这跟SVD有啥关系？

一开始说到隐约记得当时时间PCA的时候用到了SVD，但通过上面的推到我们发现需要的是特征值分解，这又是怎么回事呢？
首先来看SVD的解释：奇异值分解

X=UΣV∗,
其中U是m×m阶酉矩阵；Σ是m×n阶非负实数对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作X的奇异值分解

并且：

在矩阵M的奇异值分解中
X=UΣV∗,
1. V 的列（columns）组成一套对 X 的正交”输入”或”分析”的基向量。这些向量是 XTX 的特征向量。
2. U 的列（columns）组成一套对 X 的正交”输出”的基向量。这些向量是 XXT 的特征向量。
3. Σ 对角线上的元素是奇异值，可视为是在输入与输出间进行的标量的”膨胀控制”。这些是 XXT 及 XTX 的特征值的非零平方根，并与U和V的行向量相对应。

我们看到了熟悉的”特征向量”,还是 XTX 和 XXT 的，毫无疑问这个的结果能直接用于PCA降维。
上面这几句话都是可以推导出来的，在展开之前我们看两段代码，表示了SVD在PCA中两种不同用法：

def pca_04(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    M,N=X.shape
    Sigma=np.dot(X.transpose(),X) #这里直接去掉/(M-1)方便和pca_05比较，对求得特征向量无影响
    U,S,V = sp.linalg.svd(Sigma);
    eigVal,eigVec = S,U
    #do reduction with eigVal,eigVec

可以看到在pca_03的基础上我们把sp.linalg.eig改用了sp.linalg.svd，这涉及到：
结论1：协方差矩阵（或 XTX ）的奇异值分解结果和特征值分解结果一致。

---

def pca_05(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    U, S, V = sp.linalg.svd(X)
    eigVal,eigVec = S,V
    #do reduction with eigVal,eigVec

我们直接使用了去中心化后的SVD分解结果用于PCA降维，也是正确的，因为：
结论2： V 的列（columns）组成一套对 X 的正交”输入”或”分析”的基向量。这些向量是 XTX 的特征向量。

---

首先我们需要推导出结论2：

根据奇异值分解的定义：

X=UΣVT

则

XTX=VΣUTUΣVT=VΣ2VT=VΣ2V−1

Σ 是对角矩阵，U是标准正交基（酉矩阵），V是标准正交基（ VVT=I;V=V−1 ）
而又有 XTX 是一个对称的半正定矩阵,它可以通过特征值分解为（ Λ 是对角化特征值， Q 是特征向量）：

XTX=QΛQ−1

可以看到上下两个形式保持了一致，当限定了特征值的顺序后，这样的组合是唯一的，所以 结论2是成立的： V 是 XTX 的特征向量，奇异值和特征值是平方关系

V=QΛ=Σ2

奇异值和特征值的平方关系这个结论可以通过运行pca_04和pca_05验证：

PCA_04:
eigVal：[ 21.60311815 8.77188185]
eigVec： [[-0.88734696 -0.46110235]
[-0.46110235 0.88734696]]

PCA_05:
eigVal：[ 4.64791546 2.96173629]
eigVec： [[ 0.88734696 0.46110235]
[-0.46110235 0.88734696]]
#注意PCA_05结果中特征向量维度的符号，和上面不太一样，但这不影响降维的功能，每一列是一组基

对于结论一：

我们对 XTX 进行SVD分解(为了加以区分，下标为2)：

XTX=U2Σ2VT2

由于SVD分解的性质中的第二条

1. U 的列（columns）组成一套对 X 的正交”输出”的基向量。这些向量是 XXT 的特征向量。

所以 U2 是矩阵 XTXXTX 的特征向量，而由：

XTXXTX=U2Σ2VT2(U2Σ2VT2)T=U2Σ22UT2

根据矩阵的特征值分解：

XTX=Q2Λ2Q−12XTXXTX=Q2Λ22Q−12

所以有：

U2=Q2Σ2=Λ2

能得到这样的结果是因为 XTX 本身是对称的半正定矩阵。

用SVD有啥好处？

很多地方对PCA的实现都是使用的SVD，这样做的优点有哪些呢？从这里看到一些解释
一来因为SVD没有计算 XTX 这一步，而矩阵中一些非常小的数容易在平方中丢失
二来在一些实现中，SVD的速度比特征值分解要快很多，充分地利用了协方差矩阵的性质。

PCA和SVD的应用

PCA是不必多说，一提到降维方法首先想到的就是PCA，关于降维方法后面可能还会找时间整理一些有意思的算法，我们可以看到对这些算法都有很intuitive的解释，搞懂是如何从intuition到公式再到计算步骤，是一个非常有意思的过程。如果只是停留在了解算法思想和流程，然后拿着库用一用，会丢掉很多有意思的东西。
除了常规的PCA，好像还有一些PCA的改进算法（从PRML的目录看起来^_^），等后面有时间研究一下一并奉上（如果有意思）。

SVD其实是众多矩阵分解的一种，除了在PCA上使用，也有用于推荐，在推荐领域的svd算法形式上并不能和标准的奇异值分解对应上，但其思路是相通的，具体可以参考协同过滤算法实现。同时SVD也可以很方便地算出矩阵的伪逆，这在最小二乘中有应用：

X−1=VΣ−1UT

总结

PCA有很好的直觉解释，一些可视化也很直观，所以往往忽视了其中的一些细节，深入地了解下来发现了很多有意思的东西，很有收获。笔者水平有限，如果文中有什么错误，还请告知，不甚感谢。