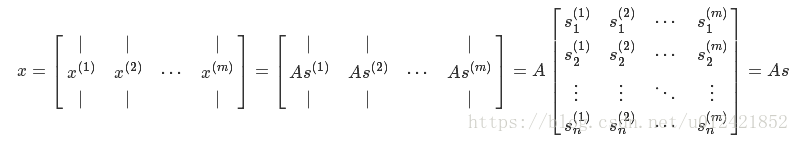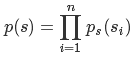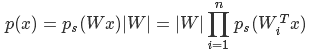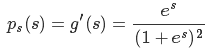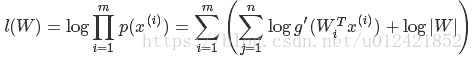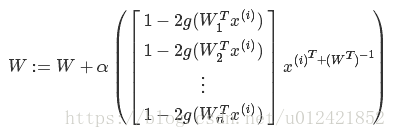ICA(独立成分分析)(2)
转载于:https://blog.csdn.net/u012421852/article/details/80500940
前情提示:ICA算法成立的前提是:假设每个人发出的声音信号各自独立。
1.鸡尾酒宴会问题
n个人在一个房间开party,房间的不同配置摆放了n个声音接收器,每个接收器在每个时刻同时采集到n个人声音的重叠声音。每个接收器和每个人的距离是不一样的,所以每个接收器接收到的声音的重叠情况也不同。party结束后,我们得到m个声音样例,每个样例是在具体时刻t,从n个接收器接采集的一组声音数据(一个接收器得到一个数据,所以有n个数据),如何从这m个样本集分离出n个说话者各自的声音呢?
2.问题数字化
首先把m个声音样例就是一个样本集X,shape=(m, n),则行表示m个样例,n表示每个样例有n个数据,n个数据是由n个接收器在当前时刻接收到的信号数据。
2.1样本集数字化
X=![]()
其中i表示在时刻i的样例,1~n表示第1~n个接收器采集的数据,一个样例就是在时刻i从n个接收器采集到的信号数据组成的。
2.2每个说话者的独立声音数字化
假设我们最后分离出来的n个说话者的声音组成的样本集是s,s中每个元素都是每个人的独立声音,可以如下表示s:
![]()
1~n表示第几个说话者的声音数据,每一维都是一个人的声音信号,每个人发出的声音信号独立
2.3目标问题的公式数字化
则一定存在一个矩阵A,使得X=As成立,数字化形式如下所示:
可知shape(X)=(n,m), shape(A)=(n,n), shape(s)=(n,m)
对上面公式解释一下:
x是一个矩阵,由m个列向量组成,每个列向量是一个时刻采集的样例![]()
![]()
可知样本集X:每个时刻t的样例有n个声音数据,每个数据是此时刻n个说话者的声音数据的线性组合。这句话理解了,就可以容易理解X=As公式了。其中A是一个未知的混合矩阵(Mixing Matrix),就是用来组合叠加信号s的。混合矩阵A就是提供"线性组合"功能的,如果知道了A就轻松求出了s,因为X是party已采集的样本集,是已知的。
现在的任务就是根据X求出A和s,没错,这听起来太扯了,确实很扯,哈哈,但是ICA可以搞定这么扯的事情。
这个比较扯的事情,还有个学名,叫盲信号分离:
知道n个说话者的混合声音的样本集X,求出混合矩阵A和每个说话者的独立声音数据s的过程,称为盲信号分离。
2.4每个时刻的样例=n个说话者的独立声音线性组合
这个就是对![]() 的示例具体化,让其更容易理解,举例如下:
的示例具体化,让其更容易理解,举例如下:
看过上面手稿示例,应该已经理解每个时刻的每个声音接收器接收到的声音都是此时刻n个说话者的独立声音的线性组合,而混合矩阵A决定了这个线性组合。
2.5决定线性组合的混合矩阵W的数字化
第一要务:此时存在公式s=WX,如果我们知道了W就可以求出s了,我们现在的任务就是想法设法求出W
3.ICA计算过程的原理推理
假设我们的随机变量有概率密度函数(连续值是概率密度函数,离散值是概率)。为了简单,我们再假设是实数,还有一个随机变量,和都是实数。令是x的概率密度,那么怎么求?
计算过程的原理推理用到的数学点都在前面文章详细介绍过了,具体请看:【机器学习】【ICA-1】概率统计/代数知识详解:高斯分布、概率密度函数、累积分布函数、联合分布函数、复合函数的概率密度函数、行列式求导等
这里面就直接给出推理结论,不再详细介绍相关函数的推导过程。
3.1 s的累积分布函数CDF(s)
累积分布函数一般用大写的CDF来标记。我们将s的累积分布函数记作g(s)。
根据累积分布函数的性质,可以知道g(s)一定满足如下两个条件:
-
(
1)g(s)单调递增
-
(
2)g(s)∈[
0,
1]
3.2 s的概率密度函数pdf(s)
概率密度函数,一般以小写的pdf标记。我们将s的概率密度函数记作![]()
现在有公式X=As,可以X是s的复合函数,则X的概率密度函数![]() 为:
为:
注:其中的Fx(x)是X的累积分布函数,用到了一维随机变量的概率密度函数等于累积分布函数的导数
3.3 s的联合分布函数
s是多维随机变量,假设每个人发出的声音信号是各自独立的,则s的联合分布函数p(s)公式为:
3.4 X的联合分布函数
因为已经知道了X的概率密度函数,则X的联合分布函数为:
3.5 给s的累积分布函数g(x)选取一个合理模型函数
已知公式s=WX,但是s和W都未知,我们需要知道s的概率密度函数![]() ,因为概率密度函数pdf是由累计分布函数CDF求导得到,如果知道了CDF,然后对其求导就可以知道了pdf。因为s和W都未知,也是没有先验知识。所以我们找一个满足CDF性质的函数作为s的pdf。
,因为概率密度函数pdf是由累计分布函数CDF求导得到,如果知道了CDF,然后对其求导就可以知道了pdf。因为s和W都未知,也是没有先验知识。所以我们找一个满足CDF性质的函数作为s的pdf。
发现sigmoid函数非常符合累积分布函数CDF的条件。(1)定义域从-∞到+∞,且在定义域内单调递增(2)值域∈[0,1]
好,我们假设s的累积分布函数g(s)为sigmoid:
对g(s)求导得到s的概率密度函数:
知道了s的概率密度函数后,下面开始求W。
3.6. 样本对数似然估计
对于给定的训练样本集X=![]() ,其对数似然估计:
,其对数似然估计:
行列式|W|求导结果为:
![]() 求导结果为:
求导结果为:
![]()
最后求得W的梯度上升的迭代计算公式为,其中α是梯度上升速率,即学习步长,可以人为指定:
然后利用上面这个W迭代计算公式进行迭代计算,直到前后计算的W的误差小于你自己指定的一个误差阈值,就可以停止迭代计算了,求出的W就是目标W,或者指定一个最大迭代次数。
3.7已知W求s
很简单,s=WX,带入W,经过np.dot(W, X)矩阵乘积计算就得到s,就是party上n个说话者各自的独立声音信号!
到此已经将ICA的计算原理推理过程全部写完了,友情提示别被累积分布函数CDF,概率密度函数pdf,联合分布函数/分布函数给迷惑了,如果迷惑了百度一下,就ok了,了解了每个定义的含义和意义就不容易混淆了。
4.为什么说ICA不适用于信号服从高斯分布的情况
此部分from:https://blog.csdn.net/xuyanan3/article/details/50475450
还有一种ICA不适用的情况,那就是信号不能是高斯分布的。假设只有两个人发出的声音信号符合多值正态分布,![]() ,I是2*2的单位矩阵,s的概率密度函数就不用说了吧,以均值0为中心,投影面是椭圆的山峰状(参见多值高斯分布)。因为
,I是2*2的单位矩阵,s的概率密度函数就不用说了吧,以均值0为中心,投影面是椭圆的山峰状(参见多值高斯分布)。因为![]() ,因此,x也是高斯分布的,均值为0,协方差为
,因此,x也是高斯分布的,均值为0,协方差为![]() 。
。
令R是正交阵![]() ,
,![]() 。如果将A替换成A’。那么
。如果将A替换成A’。那么![]() 。s分布没变,因此x’仍然是均值为0,协方差
。s分布没变,因此x’仍然是均值为0,协方差![]() 。
。
因此,不管混合矩阵是A还是A’,x的分布情况是一样的,那么就无法确定混合矩阵,也就无法确定原信号。
5.ICA算法的预处理:矩阵中心化+漂白
此部分主要参考文章: https://blog.csdn.net/xuyanan3/article/details/504754505.1矩阵中心化
也就是求x均值,然后让所有x减去均值,这一步与PCA一致。
这个可以参看以前写的文章:【机器学习】【线性代数】均值,无偏估计,总体/样本方差,样本标准差,矩阵中心化/标准化、协方差,正/不/负相关等,协方差矩阵
5.2漂白
漂白目的是将x乘以一个矩阵变成![]() ,使得
,使得![]() 的协方差矩阵是
的协方差矩阵是![]() 。解释一下吧,原始的向量是x。转换后的是
。解释一下吧,原始的向量是x。转换后的是![]() 。
。
![]() 的协方差矩阵是
的协方差矩阵是![]() ,即
,即
![]()
我们只需用下面的变换,就可以从x得到想要的![]() 。
。
其中使用特征值分解来得到E(特征向量矩阵)和D(特征值对角矩阵),计算公式为
![]()
5.3漂白的图形直观描述
假设信号源s1和s2是独立的,比如下图横轴是s1,纵轴是s2,根据s1得不到s2。
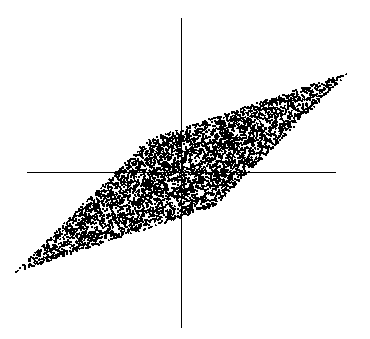
我们只知道他们合成后的信号x,如下
此时x1和x2不是独立的(比如看最上面的尖角,知道了x1就知道了x2)。那么直接代入我们之前的极大似然概率估计会有问题,因为我们假定x是独立的。因此,漂白这一步为了让x独立。漂白结果如下:
可以看到数据变成了方阵,在![]() 的维度上已经达到了独立。然而这时x分布很好的情况下能够这样转换,当有噪音时怎么办呢?可以先使用前面提到的PCA方法来对数据进行降维,滤去噪声信号,得到k维的正交向量,然后再使用ICA。
的维度上已经达到了独立。然而这时x分布很好的情况下能够这样转换,当有噪音时怎么办呢?可以先使用前面提到的PCA方法来对数据进行降维,滤去噪声信号,得到k维的正交向量,然后再使用ICA。
参考文献
[1]https://www.cnblogs.com/NaughtyBaby/p/5433672.html
[2]https://blog.csdn.net/sinat_37965706/article/details/71330979
[3]https://blog.csdn.net/xuyanan3/article/details/50475450
(end)
读后:
有几个地方在阅读的时候没弄懂,反复阅读后才弄懂,怕以后再看时还是在这里卡住,所以特地在这里将这几个地方进行说明:
第一个地方:

这里s是个向量是多个变量 s 1 , s 2 , . . . , s n s_1,s_2,...,s_n s1,s2,...,sn即不同的speaker组成的向量。这里 p s ( s i ) p_s(s_i) ps(si)只是单个speaker的概率密度函数,所以其概率密度函数的乘积就是向量s的概率密度(联合概率密度)。
第二个地方:

这里的 p x ( x ) p_x(x) px(x)指的是联合概率密度即向量x的概率密度,同样 p s ( W x ) p_s(Wx) ps(Wx)也是联合概率密度。
第三个地方:

前两个地方弄明白后,这个地方就顺理成章了,不过这里有几个地方拜我搞糊度了。
p x ( x ) = p s ( W x ) ∣ W ∣ = ∣ W ∣ ∏ i = 1 n p s ( W i T x i ) p_x(x)=p_s(Wx)|W|=|W|\prod_{i=1}^{n}p_s(W_i^Tx_i) px(x)=ps(Wx)∣W∣=∣W∣i=1∏nps(WiTxi)
我理解的是上面的式子。
第四个地方:
信号的白化,信号为什么要白化,白化的作用是啥一直恍恍惚惚。
白色向量:若一零均值的随机向量Z=(Z1,Z2,…Zm),满足E{Z*Z’}=I,I为单位矩阵,我们称这个向量为白色向量。
就是使得数据的协方差矩阵为单位阵,当协方差为单位阵时,数据各特征之间的协方差就是不相关的了。这和PCA很像,不过PCA会降维,而白化不会,且白化要求协方差矩阵是单位阵。
(end)