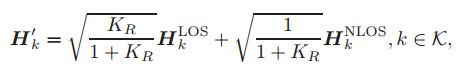多天线MIMO无线信道中，已知CSI时，关于莱斯信道（瑞利信道）矩阵的MATLAB代码。

莱斯分布（Rice distribution或Riciandistribution）是一种连续概率分布，用于在概率论与数理统计领域中，以美国科学家斯蒂芬·莱斯 [1]  （Stephen O. Rice）的名字命名。

瑞利分布（Rayleigh Distribution）:当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。【来自百度】

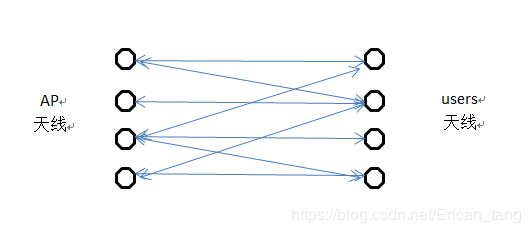
如图是一个MIMO系统，发射端和接收端都是多个天线，所以在信道上，对于每一个发送天线都有4个到接收天线的信道，这样的一个信道可以用一个4X4的信道矩阵H来表示信道增益。那么问题是在MATLAB上怎样描述这个信道矩阵？

作为无线通信研究生的初学者，我纠结了几个月都没有完全弄明白，网络上也没有关于MIMO莱斯信道矩阵的直接例子，所以我都是从SISO信道中慢慢摸索（是个渣渣），才有了一些认识，这里先作一个初级的记录吧，后面还有关于天线排列方式的不同（比如：线性排列）而令信道矩阵的每个元素有相位上的一些小变化的讲述，这里只假设AP与users之间距离很远，可以所有的天线可以看成为集成在一个点上。

瑞利信号因为信号在传输过程中，由于各种空间物体的反向、散射而产生的多径信号形成的，当空间有丰富的散射源时，在接收端，接收信号可以看成是很多独立同分布的信号的和，运用中心极限定理，可以知道，这样一个信号的幅值服从高斯分布，而其辐角也因为信号从360度过来，而服从【0，2pi】的均匀分布，所以瑞利信道可以看是两个正交的高斯随机信号组成，即作为复信号，可以令实部和虚部都是从服从N(0,1)的高斯随机数中获得的值。（这里说不清楚啦，大概有这么些概念）

rayleigh=randn(1,1)+1i*randn(1,1);

当然，可以将一维的直接扩展到MXN维瑞利矩阵：rayleigh(M,N)=randn(M,N)+1i*randn(M,N);

莱斯信号是在瑞利信道的多径基础上，还存在着一路较强的直视LOS信号（或者较强的反射信号），所以莱斯信道增益可以看成是一个LOS和一个瑞利的叠加。

即：

可见上式中，H由两部分组成，H^Los和H^NLos，其中前者为直视信道矩阵分量，后者为瑞利分量（即上面的rayleigh(M,N)）。

H^Los可以直接设为全1矩阵，这时是粗略地把AP的天线所有天线看成集中在一点处，如果自己的仿真对这些精度问题不是很在意可以用，但如果是仿真信道的，就要精确到每根天线之间的距离和角度差问题（后面再补充吧）。上式中K_R是莱斯因子，是直视信号分量和非直视多径分量总和（瑞利）信号的功率比值，一般可根据要求设，其可控制H矩阵从瑞利到莱斯信道之间的转换，当其分别趋于0和正无穷时会有瑞利和LOS信道之间的转变。

先上代码：

function [ H ] = rice_matrix(Kdb,M,N)
% H = a*H_los + b*H_nlos
% a^2 + b^2 = 1
% K is the rician factor, denoting as the ratio of the LOS amplitude to the
% rayleigh component
% When K = 0, then rice matrix is reduced to rayleigh matrix.
K=10^(Kdb/10);
H_los=ones(M,N);%LOS

H_nlos=(randn(M,N)+1i*randn(M,N))/sqrt(2);%rayleigh
H=sqrt(K/(K+1))*H_los+sqrt(1/(1+K))*H_nlos;
end  

注意：以上函数只包含了莱斯或瑞利的效应影响，如果仿真还有其它影响，比如信号关于距离的衰落，还要将矩阵乘上衰落 。

可见信道矩阵中由N(0,1)的randn( )函数中得到，其具有随机性，所以在仿真时有一个小点要注意，就是如果要多次使用这个rice_matrix函数时，每次产生的信道矩阵不相同，不可以直接用于一个参数的比较（比较接收功率），会出现仿真曲线是在一个平均值上的上下跳动的情况，所以要跑多些次数数据，然后取数据的平均值来画图即可稳定。当然，也可以只使用一次信道矩阵的生成函数，然后后面都只用这一个数据。

是不是很简单？但就是很不懂呀。气！应该还有很多地方说得不对的，请大神们指出，错得离谱的可以大骂，谢谢。