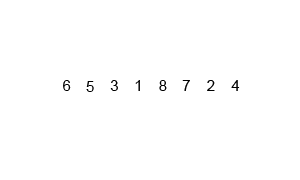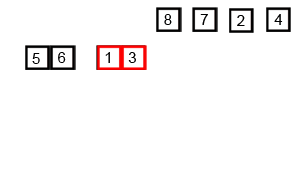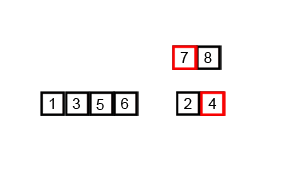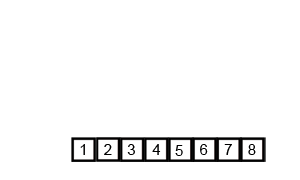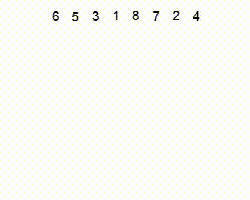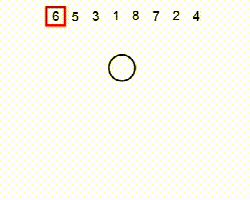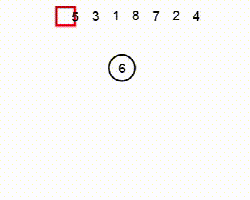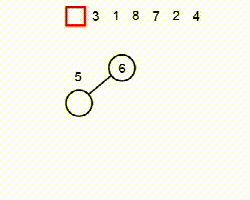Github 标星 3w+，热榜第一，使用Python实现所有算法！

学会了Python基础知识，想进阶一下，那就来点算法吧！毕竟编程语言只是工具，结构算法才是灵魂。

新手如何入门Python算法？

几位印度小哥在GitHub上建了一个各种Python算法的新手入门大全。从原理到代码，全都给你交代清楚了。为了让新手更加直观的理解，有的部分还配了动图。

标星已经达到2.7W

给出Github地址☟

https://github.com/TheAlgorithms/Python

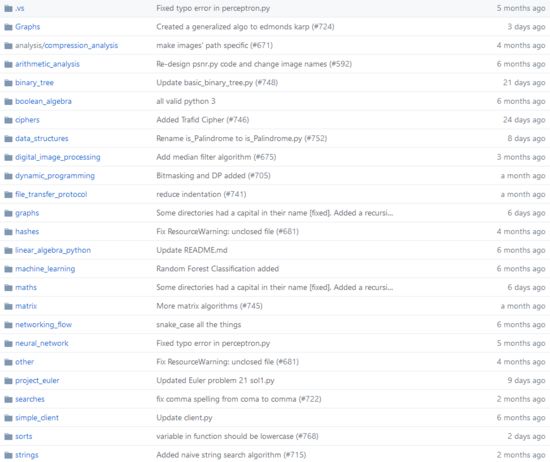
这个项目主要包括两部分内容：一是各种算法的基本原理讲解，二是各种算法的代码实现。

算法的代码实现

算法的代码实现给的资料也比较丰富，除了算法基础原理部分的Python代码，还有包括神经网络、机器学习、数学等等代码实现。

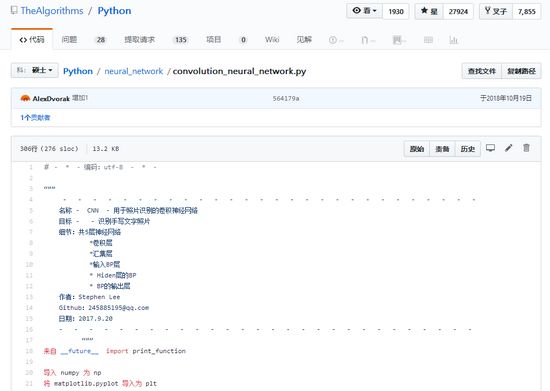
例如在神经网络部分，给出了BP神经网络、卷积神经网络、全卷积神经网络以及感知机等。

卷积神经网络代码示例

代码以Python文件格式保存在Github上，需要的同学可以自行保存下载。

再次给出github地址：

https://github.com/TheAlgorithms/Python

算法原理

在算法原理部分主要介绍了排序算法、搜索算法、插值算法、跳跃搜索算法、快速选择算法、禁忌搜索算法、加密算法等。

当然，除了文字解释之外，还给出了帮助更好理解算法的相应资源链接，包括维基百科、动画交互网站链接。

例如，在一些算法部分中，其给出的动画交互链接，非常完美帮助理解算法的运行机制。

交互动画地址：

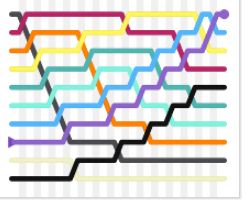
https://www.toptal.com/developers/sorting-algorithms/bubble-sort

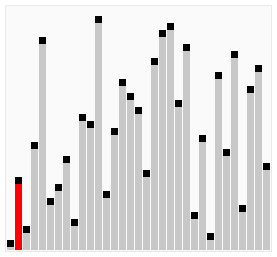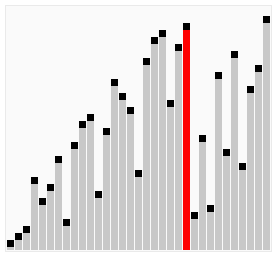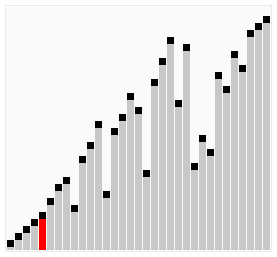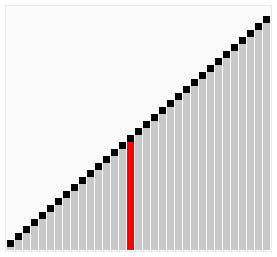
排序算法

冒泡排序

冒泡排序，有时也被称做沉降排序，是一种比较简单的排序算法。这种算法的实现是通过遍历要排序的列表，把相邻两个不符合排列规则的数据项交换位置，然后重复遍历列表，直到不再出现需要交换的数据项。当没有数据项需要交换时，则表明该列表已排序。

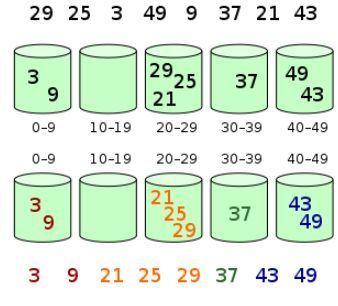
桶排序算法

桶排序(Bucket sort) 或所谓的箱排序，是一个 排序算法 ，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序，有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序。

鸡尾酒排序

鸡尾酒排序，也就是定向冒泡排序，鸡尾酒搅拌排序，搅拌排序（也可以视作选择排序的一种变形），涟漪排序，来回排序或快乐小时排序，都是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。

译者注：

鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低，而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的性能，原因是冒泡排序只从一个方向进行比对（由低到高），每次循环只移动一个项目。

以序列(2,3,4,5,1)为例，鸡尾酒排序只需要访问一次序列就可以完成排序，但如果使用冒泡排序则需要四次。但是在随机数序列的状态下，鸡尾酒排序与冒泡排序的效率都很差劲。

插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序的额外空间的排序，因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

归并排序

归并排序（Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为O(n log n)（大O符号）。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

堆（Heap）

堆（Heap）是一种基于比较的排序算法。它可以被认为是一种改进的选择排序。它将其输入划分为已排序和未排序的区域，并通过提取最大元素,将其移动到已排序区域来迭代缩小未排序区域。

译者注：

Heap 始于 J._W._J._Williams 在 1964 年发表的堆排序（heap sort），当时他提出了二叉堆树作为此算法的数据结构。

在队列中，调度程序反复提取队列中第一个作业并运行，因为实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。

基数排序

基数排序（Radix sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机（Tabulation Machine）上的贡献。

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

Shell排序

ShellSort是插入排序的一种推广，允许交换相距很远的项。思路是安排元素列表，以便从任何地方开始，考虑到每个第n个元素都会给出一个排序列表。这样的列表叫做h排序。等效地，可以被认为是h交错列表，每个元素都是单独排序的。

拓扑

拓扑排序或有向图的拓扑排序是其顶点的线性排序，使得对于从顶点u到顶点v的每个有向边uv，u在排序中位于v之前。例如，图的顶点可以表示要执行的任务，并且边可以表示一个任务必须在另一个之前执行的约束；在这个应用程序中，拓扑排序只是任务的有效序列。当且仅当图形没有有向循环时，即，如果它是有向非循环图，则拓扑排序是可能的（DAG）。任何DAG都具有至少一个拓扑排序，并且已知算法用于在线性时间内构建任何DAG的拓扑排序。

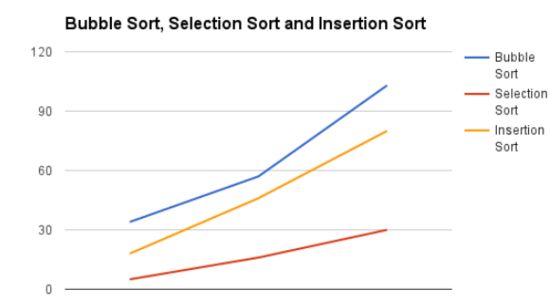
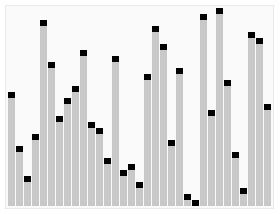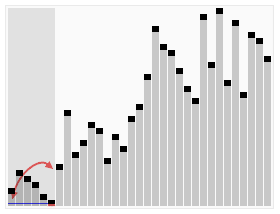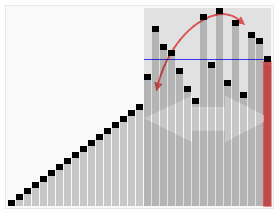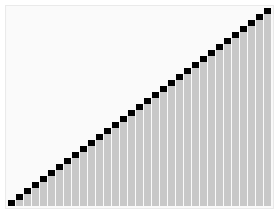
时间复杂折线图

比较排序算法的复杂性（冒泡排序，插入排序，选择排序）

比较排序算法：

Quicksort是一种非常快速的算法，但实现起来相当棘手。Bubble sort是一种慢速算法，但很容易实现。为了对小数据集进行排序，冒泡排序可能是一个更好的选择。

搜索算法

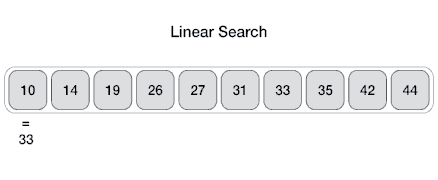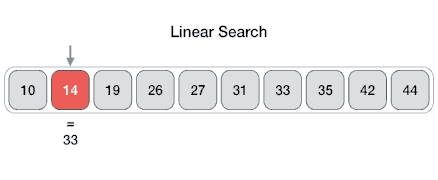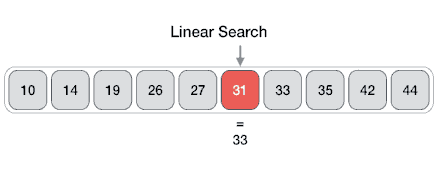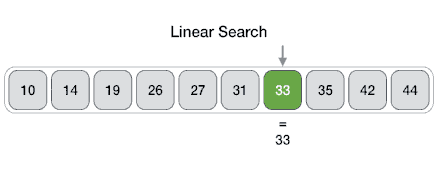
线性搜索

线性搜索或顺序搜索是用于在列表中查找目标值的方法。它按顺序检查列表中的每个元素的目标值，直到找到匹配或直到搜索完所有元素。

假设一个数组中有N个元素，最好的情况就是要寻找的特定值就是数组里的第一个元素，这样仅需要1次比较就可以。而最坏的情况是要寻找的特定值不在这个数组或者是数组里的最后一个元素，这就需要进行N次比较。

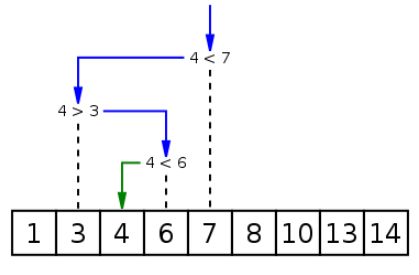
Binary 二进制搜索

二进制搜索，也称为半间隔搜索或对数搜索，用于查找已排序数组中目标值的位置。它将目标值与数组的中间元素进行比较，如果它们不相等，则目标的一半被消除，并且在剩下的一半上继续搜索直到成功。

插值搜索

插值搜索是一种用于搜索已按照键值的数值排序的数组中键的算法。

最先由WW Peterson在1957年描述。插值搜索类似于人们在电话目录中搜索名称的方法（用于订购书籍条目的关键值）：在每个步骤中，算法计算剩余搜索空间中的位置，基于搜索空间边界处的键值和所寻找的键的值，通常可以通过线性插值来寻找项目。

相比之下，二进制搜索总是选择剩余搜索空间的中间，丢弃一半或另一半，这取决于在估计位置找到的密钥与所寻找的密钥之间的比较。剩余的搜索空间缩小到估计位置之前或之后的部分。线性搜索仅使用相等性，因为它从一开始就逐个比较元素，忽略任何排序。

平均插值搜索使得log（log（n））比较（如果元素均匀分布），其中n是要搜索的元素的数量。在最坏的情况下（例如，键的数值以指数方式增加），它可以构成O（n）比较。

在插值顺序搜索中，插值用于查找正在搜索的项目附近的项目，然后使用线性搜索来查找确切项目。

跳转搜索

跳转搜索是指有序列表的搜索算法。它首先检查所有项目的Lkm，其中K∈N，并且m是块大小，直到找到大于搜索关键字的项目。为了在列表中找到搜索关键字的确切位置，在子列表L[（k-1）m，km]上执行线性搜索。

m的最优值是√n，其中n是列表L的长度。因为算法的两个步骤最多都是√n项，所以算法在O（√n）时间内运行。这比线性搜索更好，但比二分搜索差。优于后者的优点是跳转搜索只需要向后跳一次，而二进制可以向后跳转到记录n次。

在最终执行线性搜索之前，可以通过在子列表上执行多级跳转搜索来修改算法。对于k级跳跃搜索，第l级的最佳块大小ml（从1开始计数）是n（k1）/k。修改后的算法将执行k个向后跳转并在O（kn1/（k+ 1））时间内运行。

快速选择算法

快速选择（Quicksort）是一种从无序列表找到第k小元素的选择算法。它从原理上来说与快速排序有关。与快速排序一样都由托尼·霍尔提出的，因而也被称为霍尔选择算法。同样地，它在实际应用是一种高效的算法，具有很好的平均时间复杂度，然而最坏时间复杂度则不理想。快速选择及其变种是实际应用中最常使用的高效选择算法。

快速选择的总体思路与快速排序一致，选择一个元素作为基准来对元素进行分区，将小于和大于基准的元素分在基准左边和右边的两个区域。不同的是，快速选择并不递归访问双边，而是只递归进入一边的元素中继续寻找。这降低了平均时间复杂度，从O(n log n)至O(n)，不过最坏情况仍然是O(n2)。

禁忌搜索

禁忌搜索(Tabu Search,TS,又称禁忌搜寻法）是一种现代启发式算法，由美国科罗拉多大学教授Fred Glover在1986年左右提出的，是一个用来跳脱局部最优解的搜索方法。其先创立一个初始化的方案；基于此，算法“移动”到一相邻的方案。经过许多连续的移动过程，提高解的质量。

密码

凯撒密码

凯撒密码，也称为凯撒密码，移位密码，凯撒代码或凯撒移位，是最简单和最广为人知的加密技术之一。

它是一种替换密码，其中明文中的每个字母都被字母表中的一些固定数量的位置的字母替换。例如，左移3，D将被A替换，E将变为B，依此类推。

该方法以Julius Caesar的名字命名，最初是他在私人通信中使用了它。由Caesar密码执行的加密步骤通常作为更复杂的方案的一部分，例如Vigenère密码，并且仍然在ROT13系统中具有现代应用。与所有单字母替换密码一样，Caesar密码很容易破解，在现代实践中基本上没有通信安全性。

Vigenère密码

Vigenère密码是一种通过使用基于关键字字母的一系列交织的凯撒密码来加密字母文本的方法。它是一种多字母替代形式。

Vigenère密码该方法最初由Giovan Battista Bellaso在其1553年的书“La cifra del”中提出。然而，该计划后来在19世纪被误用于BlaisedeVigenère，现在被广泛称为“Vigenère密码”。

虽然该密码易于理解和实施，但三个世纪以来它一直抵制所有打破密码的企图，因此也被称为这lechiffreindéchiffrable（法语为“难以理解的密码”）。Friedrich Kasiski是第一个在1863年发表破译Vigenère密码的通用方法。

转置密码

转置密码是一种加密方法，通过该加密方法，明文单元（通常是字符或字符组）所保持的位置根据常规系统移位，使得密文构成明文的排列。也就是说，单位的顺序改变（明文被重新排序）。

在数学上，双字符函数用于加密字符的位置和用于解密的反函数。

RSA (Rivest–Shamir–Adleman)

RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。

1973年，在英国政府通讯总部工作的数学家克利福德·柯克斯（Clifford Cocks）在一个内部文件中提出了一个与之等效的算法，但该算法被列入机密，直到1997年才得到公开。

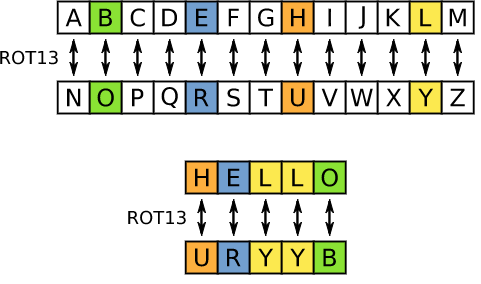
ROT13

ROT13（“旋转13个位置”，有时用连字符ROT-13）是一个简单的字母替换密码，用字母表后面的第13个字母替换一个字母。ROT13是古罗马开发的Caesar密码的特例。

因为基本拉丁字母中有26个字母（2×13），所以ROT13是自身的反转，也就是说，要撤消ROT13需要相同的算法，因此可以使用相同的动作进行编码和解码。该算法几乎不提供加密安全性，并且经常被引用为弱加密的典型示例。