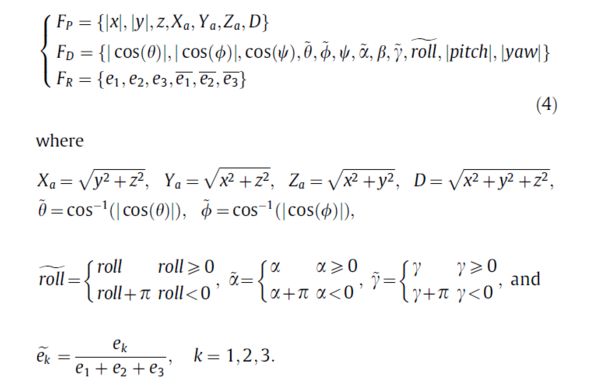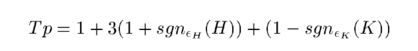3D目标识别---局部特征描述子介绍
3D目标识别研究随着深度传感器的普及逐渐受到关注,本文主要介绍了到目前为止一些经典的三维局部特征描述方法,有些地方可能不够完善或错误解读,仅供读者参考了解。后续还会继续完善。
1. 3D识别的流程图
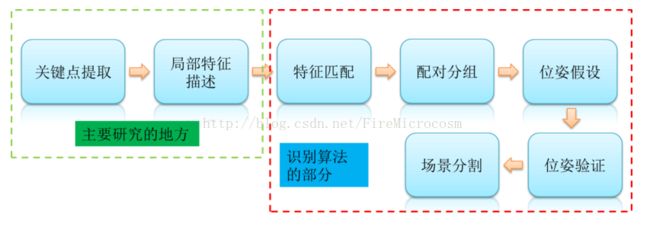
2. 局部特征描述子
- Spin Image
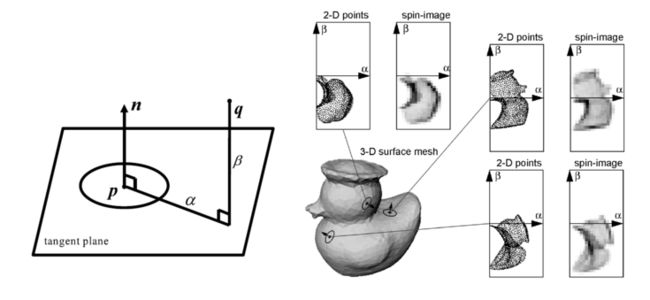
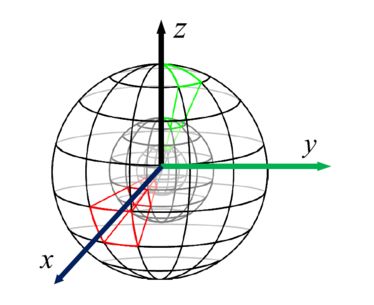
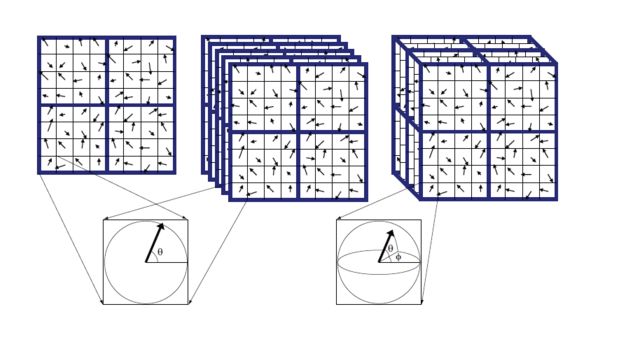
统计的是在特征点局部圆柱坐标系下的领域点2D坐标分布直方图特征。如下图所示,圆柱坐标系由特征点p的法向量n以及切平面构成。点p的所有球形领域点q在圆柱坐标系下的坐标分布形成一个2D的Points分布图,然后离散化得到spin image。离散的过程会通过双线性插值的方式平滑每个点的作用,是的该描述子具有一定的抗噪声能力。最后得到的spin image 往往还需要一个归一化步骤,通过除以自旋图中最大的像素值得到,该步骤使得自旋图描述子具有一定的抗分辨率变化的能力。
不足:
a)坐标系依赖特征点的法向量,容易受噪声干扰;
b)没有考虑领域点的方位信息,使得特异性降低。
参考文献:
[1]Johnson AE, Hebert M (1999) Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Transactions on Pattern Analysis and Machine Intelligence 21(5):433–449
- SHOT(Signature of Histograms of OrienTations)
一种结合了几何分布信息以及直方图统计信息的鲁棒性,特异性描述子。具体的实现步骤如下:
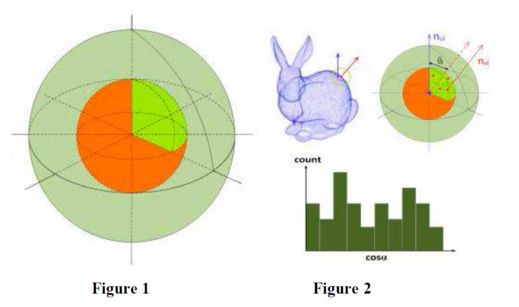
step1: 根据特征点球邻域信息建立局部参考坐标系LRF,对特征点的球邻域分别沿径向(内外球)、经度(时区)和纬度方向(南北半球)进行区域划分。通常径向划分为2,经度划分为8,纬度划分为2,总共32个小区域。
step2:分别统计每个小区域内的法向量夹角余弦值分布情况,法向量划分为11个bin。最终SHOT的长度为:32x11=352。
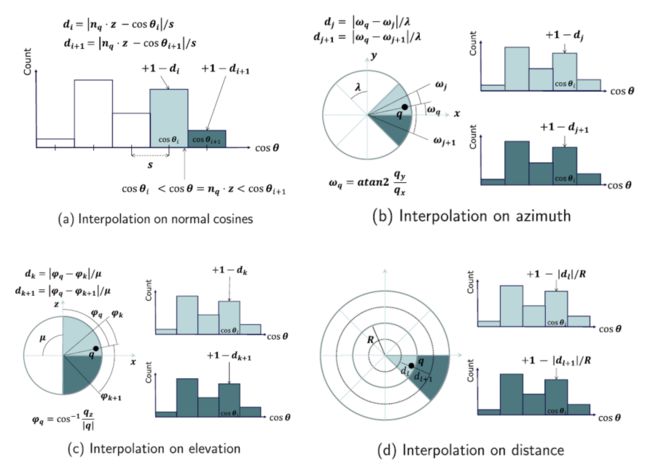
step2具体实现细节:采用双线性插值统计每个区域中的直方图特征
参考文献:
[1]Tombari, Federico, Samuele Salti, and Luigi Di Stefano. "Unique signatures of histograms for local surface description." European conference on computer vision. Springer Berlin Heidelberg, 2010.
[2]Salti S, Tombari F, Di Stefano L. SHOT: unique signatures of histograms for surface and texture description[J]. Computer Vision and Image Understanding, 2014, 125: 251-264.
- RoPS
通过统计领域点在局部坐标系LRF三个平面的投影分布图的某些图像特征信息所构建的1D直方图特征,具体的实现步骤如下:
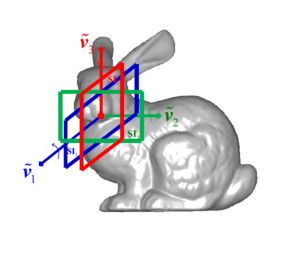
step1: 由特征点的球领域点建立局部参考坐标系LRF
step2: 将领域点转化到局部参考坐标系LRF下,绕x轴转θk(k=1,2,...,T)。每次旋转后将领域点向三个坐标平面投影,分别获取三个投影的最小包围盒(通过计算最小和最大坐标得到)。然后将每个投影图离散为LxL的图像,计算每个图像的特征信息,包括μ11,μ21,μ12,μ22,e。其中μmn 表示图像的m,n阶中心矩,e表示香农熵。也即是每次旋转得到3个投影图像,每个图像计算5个图像特征量,则绕x轴得到的特征向量的长度为Tx3x5。
step3: 然后分别绕y轴和z轴进行同样的操作。最终得到的RoPS特征长度=3xTx3x5,T一般取值为3,则RoPS的总长度为135。
描述子的性能评价:
优点:该描述子具有很好的抗噪声和抗干扰能力,基于该描述子的3D识别算法在多个数据集上取得了state-of-the-art的识别效果
不足:依赖于LRF的鲁棒性和特异性,文中提到的LRF构建方法需要mesh数据,不能直接在点云数据上计算。描述子的计算开销大,实时性差。
参考文献:
[1]Guo Y, Sohel F, Bennamoun M, Lu M, Wan J (2013b) Rotational projection statistics for 3D local surface description and object recognition.International Journal of Computer Vision 105(1):63–86
- TriSI
spin image的一种改进,利用特征点领域点建立局部参考坐标系LRF, 然后沿着每个轴分别获取相应的spin image,得到F={SI,SI,SI}。然后利用PCA进行降维处理,通常降到95%的特征值比例。该描述子具有很好的抗噪声和抗分辨率变化的性能。建立LRF,沿着三个轴的方向得到各自的SI,一定程度上融合了领域点的方位信息。
不足:描述子的性能依赖LRF的鲁棒性和特异性。
参考文献:
[1]Guo Y, Sohel F, Bennamoun M, Lu M, Wan J (2013c) TriSI: A distinctive local surface descriptor for 3D modeling and object recognition. In: 8th International Conference on Computer Graphics Theory and Applications, pp 86–93
- 3D shape context
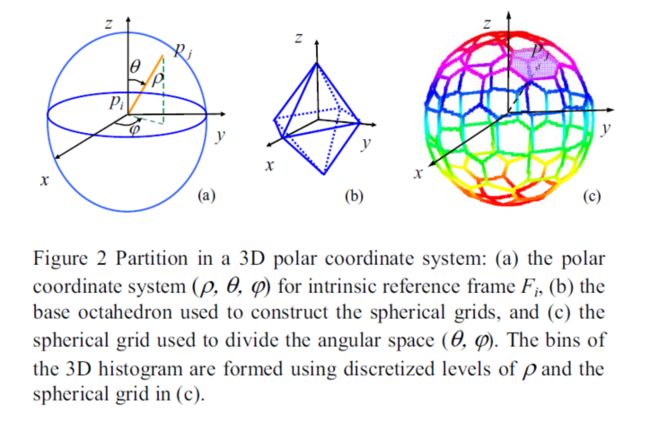
扩展自2D shape context 的一种3D局部特征描述子。具体的实现方式是以特征点的法向量为其球邻域的北极方向,然后分别沿径向(半径方向)Dsc_r,经度Dsc_a和纬度Dsc_e方向进行区域划分。然后统计落入每个区域的加权点的值的和
参考文献:
[1]Frome A, Huber D, Kolluri R, et al. Recognizing objects in range data using regional point descriptors[C]//European conference on computer vision. Springer Berlin Heidelberg, 2004: 224-237.
- Unique shape context
3D shape context 的改进版,通过建立局部参考坐标系LRF,消除3DSC 经度划分方向存在的歧义问题,提高了描述子的区分性,节省了存储空间。
参考文献:
[1]Tombari, Federico, Samuele Salti, and Luigi Di Stefano. "Unique shape context for 3D data description." Proceedings of the ACM workshop on 3D object retrieval. ACM, 2010.
- ISS(intrinsic shape signatures)
- VD-LSD
建立特征点的局部参考坐标系,然后计算邻域点在该坐标系下一系列的属性值,如下图所示:
参考文献:
[1]Taati B, Bondy M, Jasiobedzki P, et al. Variable dimensional local shape descriptors for object recognition in range data[C]//2007 IEEE 11th International Conference on Computer Vision. IEEE, 2007: 1-8.
[2]Taati B, Greenspan M. Local shape descriptor selection for object recognition in range data[J]. Computer Vision and Image Understanding, 2011, 115(5): 681-694.
- LSP(Local surface patch)
为了匹配的高效性,通过计算局部曲面的类型Surface Type 以及重心坐标值进行简单匹配,然后在进行直方图匹配。下面是surface type的计算公式:
其中H和K分别是p点的平均曲率和高斯曲率。
参考文献:
参考文献:
[1]Chen H, Bhanu B. 3D free-form object recognition in range images using local surface patches[J]. Pattern Recognition Letters, 2007, 28(10): 1252-1262.
- THRIFT
利用两个不同的球邻域估计特征点邻域内的每个点的大窗口法向量nlarge以及小窗口法向量nsmall,一般大窗口半径为0.8R,小窗口半径为0.3R,其中R是特征点的支持半径。计算每个邻域点的两个法向量的夹角θ,将它们映射到一个1D直方图中,直方图的bin一般取10,每个bin的宽度=90/10.然后将直方图归一化为单位长度向量。
参考文献:
[1]Flint, Alex, Anthony R. Dick, and Anton Van Den Hengel. "Thrift: Local 3D Structure Recognition." dicta. Vol. 7. 2007.
- PFH(Point Feature Histograms)
统计的是特征点邻域内任意点对之间的夹角以及距离特征信息,任意点对之间需要建立一个局部参考坐标系,具体细节可参照文献[1],然后将每个点对4元特征映射为一个Index值,如下式所示:
上面因为对每个特征元进行了2分(0或1),则直方图的长度为24=16,如果3分,则直方图的长度为34=81.
参考文献:
[1]Rusu R B, Marton Z C, Blodow N, et al. Persistent point feature histograms for 3D point clouds[C]//Proc 10th Int Conf Intel Autonomous Syst (IAS-10), Baden-Baden, Germany. 2008: 119-128.
- FPFH(Fast Point Feature Histogram)
PFH计算开销很大,存在很多重复性的计算。因为邻域点对存在大量重叠,FPFH是对PFH的改进,使得计算效率从O(nk2)降到了O(nk),同时保留了PFH的描述性。具体的实现步骤如下:
step1: 计算p点邻域内与之直接相连的所有点对特征,生成Simplified Point Feature Histogram(SPFH)。
step2: 计算邻域内其他点的SPFH特征。
step3: p点的FPFH特征由邻域内的所有点的SPFH特征加权得到。
[1]Rusu R B, Blodow N, Beetz M. Fast point feature histograms (FPFH) for 3D registration[C]//Robotics and Automation, 2009. ICRA'09. IEEE International Conference on. IEEE, 2009: 3212-3217.
- 2.5D-SIFT
- SI-SIFT
- EM
- MeshHoG