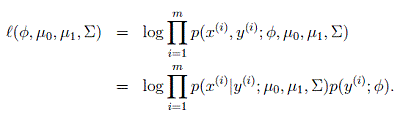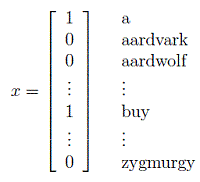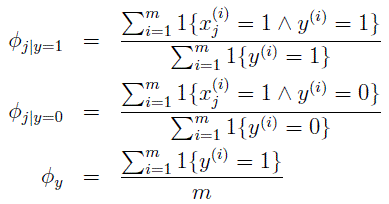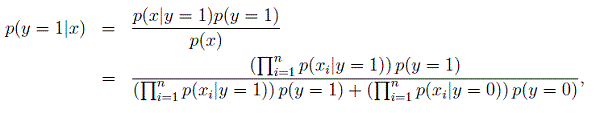判别模型(Discriminative model)和生成模型(Generative model)

在前面的章节中，我们介绍过SVM、逻辑回归，这两者都属于监督学习中的一种，即训练数据的标签是给定的，我们希望通过对训练数据进行学习，这样对于给定的新样本数据，我们可以对它的类别标签进行预测。实际上，监督学习又可以分为两类，判别模型（Discriminative model）和生成模型（generative model），前面提到的SVM和逻辑回归都属于判别模型的一种。那么判别模型和生成模型有何区别？

1.1 判别模型和生成模型的区别
我们先来看以前讲过的SVM和逻辑回归（LR）有什么特点。这两者都是对分布概率 p(y|x;θ) 进行进行学习的，这个概率表示给定一个新样本数据特征 x ，模型参数 θ 可以通过训练数据学习而来，我们期望对数据 x 的类别标签的概率分布 p(y|x;θ) 进行预测。比如，在逻辑回归中，我们对数据类别的概率分布的预测是通过模型 p(y|x;θ)=g(θTx) 进行判定的，其中 g 表示sigmod函数。这种类型的预测模型称为判别模型，它是在有限训练样本已知的条件下学习判别函数，并不会考虑样本数据产生的模型是什么样，而直接预测模型的输出。典型的判别模型包括k近邻，感知机，决策树，SVM，逻辑回归等。

考虑这样一个例子，假设给定动物的若干个特征属性，我们希望通过这些特征学习给定的一个“个体”到底是属于“大象”（y=1）还是“狗”（y=0）。如果采用判别模型的思路，如逻辑回归，我们会根据训练样本数据学习类别分界面，然后对于给定的新样本数据，我们会判断数据落在分界面的哪一侧从而来判断数据究竟是属于“大象”还是属于“狗”。在这个过程中，我们并不会关心，究竟“大象”这个群体有什么特征，“狗”这个群体究竟有什么特征。
现在我们来换一种思路，我们首先观察“大象”群体，我们可以根据“大象”群体特征建立模型，然后再观察“狗”群体特征，然后再建立“狗”的模型。当给定新的未知个体时，我们将该个体分别于“大象”群体和“狗”群体模型进行比较，看这个个体更符合哪个群体模型的特征。

所以分析上面可知，判别模型是直接学习 p(y|x) ，或者直接从特征空间学习类别标签；生成模型是对类别模型进行学习，即学习 p(x|y) (每一类别数据的特征模型)和 p(y) （别类概率）。如在上面的例子中，对于“大象”群体，特征分布可以表示为 p(x|y=1) ，对“狗”群体建立特征模型 p(x|y=0) 。假设类别概率分布 p(y) 是已知的，那么我们可以通过贝叶斯公式，对给定数据特征 x 的类别后验概率推导为，

p(y|x)=p(x|y)p(y)p(x)

其中， p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0) (每一类的类别概率乘以该类别内的特征分布概率就是总的特征分布概率)，所以 p(x) 也可以表达为模型 p(x|y) 和类别概率 p(y) 了。在进行类别判定时，我们会分别计算数据 x 属于各个别类的概率大小，并将 x 的标签赋予为概率更大的类别，也就是，

argmaxyp(y|x)=argmaxyp(x|y)p(y)p(x)=argmaxyp(x|y)p(y)

最后一个式子是因为对于所有类别的特征概率分布都是一样的，所以可以不考虑 p(x) 。 所以，实际上，生成模型是对联合概率分布 p(x,y)=p(x|y)p(y) 进行学习的。常用的生成模型有朴素贝叶斯，隐马尔可夫等，HMM等。

1.2 高斯生成模型
1.2.1高斯生成模型概念
这里首先列举一个简单的例子，高斯生成模型，也就是说每个类别的数据分布可以由高斯模型进行建模，也就是说有，

y∼Bernoulli(ϕ)

x|y=0∼N(μ0,Σ)

x|y=1∼N(μ1,Σ)

类别概率为伯努利分布。在这个问题中，所涉及到的未知参数包括： ϕ,Σ,μ0,μ1 ，参数的求解可以通过最大化联合概率分布求得，即,

最终求得的各个参数计算公式为，

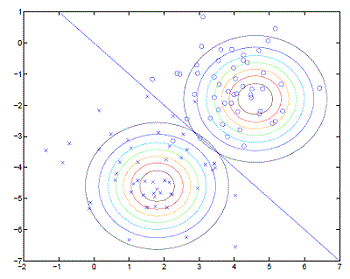
我们以图示来说明，其中，圆圈和叉号分别表示两类数据，分别使用高斯模型对数据分布进行建模，由于两个高斯模型的协方差参数是一致的，所以这两个高斯分布的形状是一样的，只是中心位置不一致而已。图示中的直线表示的是决策面，表示 p(y=1|x)=p(y=0|x)=0.5 ，表示属于两个类别的概率大小时一样的，否则的话，根据数据属于两个类别的概率大小决定数据所属于的类别。

1.2.2高斯生成模型与逻辑回归的关系
有趣的是，高斯生成模型中， p(y=1|x;ϕ,μ0,μ1,Σ) 是可以表示为 x 的函数的（这里大家可以自行推导一下）， θ 是参数 ϕ,Σ,μ0,μ1 的函数，

p(y=1|x;ϕ,μ0,μ1,Σ)=11+exp(−θTx)

而这个形式恰好是逻辑回归的基本模型！这说明，我们在使用高斯模型对每一类别的特征数据进行建模时， p(y|x) 是符合逻辑回归模型的，但是如果满足有 p(y|x) 符合逻辑回归模型，并不能一定得到数据特征分布是高斯分布这个结论，所以反向推导是不成立的！实际上，当类别数据特征分布满足如泊松分布（Poisson Distribution）时，也可以得到 p(y|x) 是满足逻辑回归模型的。

总的说来，GDA（高斯生成算法）对数据分布进行了一定的假设（假设数据分布是高斯分布的），当数据确实符合或近似符合高斯分布时，这种计算方法是比较高效准确的；但是当数据并不符合高斯分布时，这种计算方法的效果并不是很好，而逻辑回归并不存在这样的假设，所以当数据不满足高斯分布时，逻辑回归分类的效果要更好一些。

1.3朴素贝叶斯
1.3.1 朴素贝叶斯基本概念
这里介绍另外一种更为常用的模型-朴素贝叶斯（Naive Bayes）。在GDA中，特征 x 是连续值，而在朴素贝叶斯中，特征 x 是离散的。
考虑这样一个应用场景，我们需要根据邮件内容来判断该邮件是否有垃圾邮件（垃圾邮件类别标签为1，非垃圾邮件类别标签为0）。那么，首先，我们需要设计特征表示。假设我们的词库中共有500000个单词，分别是”a, aardvark, aardwolf,…,buy,…,zygmurgy”，那么我们可以建立一个长度为500000的特征向量 x ,

其中， x 的每一维度表示相应位置的单词是否出现，如果出现，则用1表示，如果未出现，则用0表示。根据生成模型的定义，对于给定的一封待检测邮件，我们需要比较 p(y=0|x) 和 p(y=1|x) 的概率大小，如果 p(y=1|x) 概率大，则说明该邮件属于“垃圾邮件”，否则属于“非垃圾邮件”。
接下来，我们需要分别分析训练数据中已有的“垃圾邮件”和“非垃圾邮件”，即 p(x|y=1) 和 p(x|y=0) 。如果考虑使用多项式对每一类中的500000维度的特征进行建模，涉及的参数太多，不合理！所以在朴素贝叶斯（NB）中，引入一个假设：在特定类别数据中， xi 之间是条件独立的，比如说在词汇表中“buy”这个单词位置是2087，“price”这个单词的位置是39831，那么我们假设如果有 y=1 ，即该邮件是“垃圾邮件”，那么“buy这个单词是否出现”这个事实，并不会影响“price”这个单词出现的概率，即有 p(x2087)=p(x2087|y,x39831)
所以概率 p(x|y) 表示为，

p(x|y)=p(x1,...,x500000|y)=p(x1|y)p(x2|y,x1)p(x3|y,x1,x2)...p(x500000|y,x1,...,x499999)=p(x1|y)p(x2|y)p(x3|y)...p(x500000|y)=∏i=1np(xi|y)

虽然NB问题具有较强假设条件，在事实上，在很多问题上，NB算法能够取得较好的效果。

在这个问题中，参数可以表示为， ϕi|y=1=p(xi=1|y=1) ， ϕi|y=0=p(xi=1|y=0) ， ϕy=p(y=1) 。那么对于给定的训练集 {(x(i),y(i))} ， i=1,...,m ，那么参数的求取可以通过最大化联合概率分布获得，联合概率分布可以表示为，

L(ϕi|y=1,ϕi|y=0,ϕy)=∏i=1mp(x(i),y(i))

联合概率分布函数分别对各个参数求导，既可以获得参数表示为，

其中， ϕj|y=1 表示解释为在所有垃圾邮件中第j个单词出现的邮件所占的比例。
在计算好这些参数之后，那么对于新的邮件，特征表示为 x ，预测该数据所属于的类别可以通过贝叶斯公式获得，即，

判定该邮件是否是垃圾邮件，则分别计算其属于垃圾邮件和非垃圾邮件的概率，哪个对应的概率大，则说明应该将该邮件分类为对应的那一类别。

所以，综合分析朴素贝叶斯的工作过程应如下，
1.设特征 x={x1,x2,...,xm} ，每一个分量表示特征的一个属性维度
2.设有类别集合 C=y1,y2,...,yn
3.分别计算特征 x 属于每一个类别的概率大小， p(y1|x),p(y2|x),...,p(yn|x)
概率大小通过贝叶斯公式计算而来， p(yi|x)=p(x|yi)p(yi)p(x)=(∏mj=1p(xj|yi)p(yi))p(x)
4.特征 x 类别为最大概率所对应的类别， argmaxyip(yi|x)

1.3.2 朴素贝叶斯例子
转自：http://www.cnblogs.com/leoo2sk/archive/2010/09/17/1829190.html
这里再列举一个例子来说明朴素贝叶斯的工作原理。使用贝叶斯分类解决实际问题的例子，问题描述为：对于SNS社区来说，不真实账号是一个普遍存在的问题，作为SNS社区的运营商，希望可以检测出这些不真实账号，从而在一些运营分析报告中避免这些账号的干扰，亦可以加强对SNS社区的了解和监管。如果通过纯人工检测，需要耗费大量的人力，效率也比较地下，如能引入自动检测机制，将大大提高工作效率。所以这个问题是来对社区中的所有账号分类为真实账号和不真实账号两个类别。

1.选取特征。
设不真实账号标签 y=1 ，真实账号标签 y=0 。
我们选择三个特征属性： x={x1,x2,x3} , x1 :日志数量/注册天数； x2 :好友数量/注册天数； x3 :是否使用真实头像。
各个属性划分范围为，
x1:x1≤0.05,0.05<x1<0.2,x1≥0.2 ， x2:x2≤0.1,0.1<x2<0.8,x2≥0.8 ， x3：x3=0（不是）,x3=1（是）

2.选取训练样本
这里使用运维人员曾经人工检测过的一万个账号作为训练样本。

3.计算类别概率 p(y)
p(y=0)=8900/10000=0.89,p(y=1)=1100/10000=0.11

4.计算每个类别的各个特征属性划分的概率

p(x1≤0.05|y=0)=0.3,p(0.05<x1<0.2|y=0)=0.5,p(x1≥0.2|y=0)=0.2

p(x1≤0.05|y=1)=0.8,p(0.05<x1<0.2|y=1)=0.1,p(x1≥0.2|y=1)=0.1

p(x2≤0.1|y=0)=0.1,p(0.1<x2<0.8|y=0)=0.7,p(x2≥0.8|y=0)=0.2

p(x2≤0.1|y=1)=0.7,p(0.1<x2<0.8|y=1)=0.2,p(x2≥0.8|y=1)=0.1

p(a3=0|y=0)=0.2,p(a3=1|y=0)=0.8

p(a3=0|y=1)=0.9,p(a3=1|y=1)=0.1

5.新样本判别
现在有一个账号：使用非真实头像( x3=0 )，日志数量与注册天数比率为0.1，好友数量与注册天数比率为0.2。那么该账号分别属于真实账号和非真实账号的概率大小可以通过联合概率大小来判定，

p(x,y=0)=p(x|y=0)p(y=0)=0.5∗0.7∗0.2∗0.89=0.0623

p(x,y=1)=p(x|y=1)p(y=1)=0.1∗0.2∗0.9∗0.11=0.00198

该账号属于类别 y=0 的概率要大一些，所以通过朴素贝叶斯方法判定该账号应属于真实账号。

如有问题，欢迎指正~