拼多多2018校招编程题汇总 - 题解
题目链接:点这儿。
列表补全
题目
在商城的某个位置有一个商品列表,该列表是由
L1、L2两个子列表拼接而成。当用户浏览并翻页时,需要从列表L1、L2中获取商品进行展示。展示规则如下:
- 用户可以进行多次翻页,用
offset表示用户在之前页面已经浏览的商品数量,比如offset为4,表示用户已经看了4个商品n表示当前页面需要展示的商品数量- 展示商品时首先使用列表
L1,如果列表L1长度不够,再从列表L2中选取商品- 从列表
L2中补全商品时,也可能存在数量不足的情况请根据上述规则,计算列表L1和L2中哪些商品在当前页面被展示了
输入描述
每个测试输入包含1个测试用例,包含四个整数,分别表示偏移量
offset、元素数量n,列表L1的长度l1,列表L2的长度l2。
输出描述
在一行内输出四个整数分别表示L1和L2的区间
start1,end1,start2,end2,每个数字之间有一个空格。
注意,区间段使用半开半闭区间表示,即包含起点,不包含终点。如果某个列表的区间为空,使用[0, 0)表示,如果某个列表被跳过,使用[len, len)表示,len表示列表的长度。
样例
in: 2 4 4 4 1 2 4 4 4 1 3 3 out: 2 4 0 2 1 3 0 0 3 3 1 2
解析
模拟题,不说了,比划一下都写得出。
代码
#include return 0;
} Anniversary
题目
拼多多王国的城市和道路的拓扑结构比较特别,是一个树状结构:
- 每个城市是树的一个节点;
- 城市之间的道路是树的一条边;
- 树的根节点是首都。
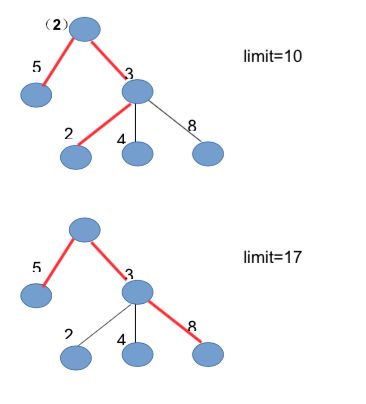
拼多多周年庆马上就要到了,这是拼多多王国的一个大日子。为了活跃气氛,国王想在道路上布置花灯。花灯可是很贵的东西,尽管国王想要在所有道路上都布置花灯,但是如果要花太多钱的话,是过不了财政大臣那一关的。国王把这个计划告诉财政大臣,最后他们商讨出来这么一个方案:
- 一条道路要么不布置花灯,要么整条布置花灯,不能选择其中的某一段布置;
- 除非没有道路通向首都,否则至少为一条通向首都的道路布置花灯;
- 所有布置花灯的道路构成的子图是连通的,这保证国王从首都出发,能通过只走布置了花灯的道路,把所有的花灯游览完;
- 如果某个城市(包括首都)有大于等于2条道路通向子城市,为了防止铺张浪费,最多只能选择其中的两条路布置花灯;
- 布置花灯的道路的总长度设定一个上限。
输入描述
每个测试输入包含1个测试用例。
输入的第一行是一个正整数m, 0<m<=9900 0 < m <= 9900 ,表示布置花灯的道路的总长度的上限。
输入的第二行是一个正整数n, n<=100 n <= 100 ,表示城市的个数。
紧接着是n-1行输入,每行三个正整数u、v、d,表示下标为u的城市有一条长度为d的道路通向它的一个子城市v,其中 0<=u<n,0<=v<n,0<d<=100 0 <= u < n , 0 <= v < n , 0 < d <= 100 。
输出描述
输出一个正整数,表示能布置花灯的道路长度的最大值
样例
in: 5 5 0 1 1 0 2 2 0 3 3 0 4 4 out: 5
解析
由于这个题加了最大值的上限,导致我只能用set去保存每棵子树可能出现的合法长度的值;
然后就枚举从一个节点所有的儿子中选1个儿子,选2个儿子的情况;
最后的答案就是set中最后一个元素的值。
代码
#include 数三角形
题目
给出平面上的
n个点,现在需要你求出,在这n个点里选3个点能构成一个三角形的方案有几种。
输入描述
第一行包含一个正整数
n,表示平面上有n个点( n<=100 n <= 100 )
第2行到第n + 1行,每行有两个整数,表示这个点的x坐标和y坐标。(所有坐标的绝对值小于等于100,且保证所有坐标不同)
输出描述
输出一个数,表示能构成三角形的方案数。
样例
in: 4 0 0 0 1 1 0 1 1 out: 4
解析
暴力枚举3个点,然后用向量的方法判断是否三点不共线就行了。
代码
#include int , int> > points(n);
for (int i = 0; i < n; cin >> points[i].first >> points[i].second, ++i) {}
for (int i = 0; i < n - 2; i++) {
for (int j = i + 1; j < n - 1; j++) {
pair<int, int> a(points[j].first - points[i].first, points[j].second - points[i].second);
for (int k = j + 1; k < n; k++) {
pair<int, int> b(points[k].first - points[i].first, points[k].second - points[i].second);
ans += a.first * b.second != a.second * b.first;
}
}
}
cout << ans << endl;
}
return 0;
}
最大乘积
题目
给定一个无序数组,包含正数、负数和0,要求从中找出3个数的乘积,使得乘积最大,要求时间复杂度: O(n) O ( n ) ,空间复杂度: O(1) O ( 1 ) 。
输入描述
第一行是数组大小
n,第二行是无序整数数组A[n]
输出描述
满足条件的最大乘积
样例
in: 4 3 4 1 2 out: 24
解析
时间复杂度: O(n) O ( n ) ,空间复杂度: O(1) O ( 1 ) 的解法是动态规划。
由于是乘积最大,因此要考虑正负对最大最小值的影响:
- 如果当前值是正数,那么乘一个最大值还是最大值
- 如果当前值是负数,那么乘一个最大值就变成最小值了,乘一个最小值才是最大值
因此这个题要维护6个变量dp_min_1, dp_min_2, dp_min_3,dp_max_1,dp_max_2, dp_max_3,分别表示选1、2、3个元素的乘积最小值,选1、2、3个元素乘积的最大值;
然后对选不选当前元素依据当前元素的正负去维护这6个变量就行了,最后的答案就是dp_max_3。
代码
#include 小熊吃糖
题目
有
n只小熊,他们有着各不相同的战斗力。每次他们吃糖时,会按照战斗力来排,战斗力高的小熊拥有优先选择权。前面的小熊吃饱了,后面的小熊才能吃。每只小熊有一个饥饿值,每次进食的时候,小熊们会选择最大的能填饱自己当前饥饿值的那颗糖来吃,可能吃完没饱会重复上述过程,但不会选择吃撑。
现在给出n只小熊的战斗力和饥饿值,并且给出m颗糖能填饱的饥饿值。
求所有小熊进食完之后,每只小熊剩余的饥饿值。
输出描述
第一行两个正整数
n和m,分别表示小熊数量和糖的数量。( n<=10,m<=100 n <= 10 , m <= 100 )
第二行m个正整数,每个表示着颗糖能填充的饥饿值。
接下来的n行,每行2个正整数,分别代表每只小熊的战斗力和当前饥饿值。
题目中所有输入的数值小于等于100。
输入描述
输出
n行,每行一个整数,代表每只小熊剩余的饥饿值。
样例
in: 2 5 5 6 10 20 30 4 34 3 35 out: 4 0
解析
模拟就好了,这个题的关键是排序,先按战斗力排序,然后处理好,最后再按出现的顺序排序输出就行了。
代码
#include