Graph Neural Network(GNN)概述
什么是GNN
GNN是Graph Neural Network的简称,是用于学习包含大量连接的图的联结主义模型。当信息在图的节点之间传播时GNN会捕捉到图的独立性。与标准神经网络不同的是,GNN会保持一种状态,这个状态可以代表来源于人为指定的深度上的信息。
图神经网络处理的数据就是图,而图是一种非欧几里得数据。GNN的目标是学习到每个节点的邻居的状态嵌入(embedding),这个状态嵌入是向量且可以用来产生输出,例如节点的标记。如下图,最终的目的就是学习到红框的H,由于H是定点,因此可以不断迭代直到H的值不再改变即停止。

近年来图神经网络受到大家越来越多的关注,在文本分类(Text classification),序列标注(Sequence labeling), 神经机器翻译(Neural machine translation),关系抽取(Relation extraction),事件抽取(Event extraction), 图像分类(Image Classification),视觉推理(Visual Reasoning),*语义分割(Semantic Segmentation)*等等领域都有了一些应用。本文主要分享先当下最为广泛的几种图神经网络的结构。参考:Tutorial on Graph Representation Learning, AAAI 2019
什么是图
图是一种对节点和节点间关系建模的数据结构,是机器学习中唯一的非欧几里得数据,图分析可用于节点分类、链接预测和聚类。
GNN就是一种在图域上操作的深度学习方法。
GNN的来源
-
CNN:CNN可以提取大量本地紧密特征并组合为高阶特征,但CNN只能够操作欧几里得数据。CNN的关键在于局部连接、权值共享、多层使用;
-
graph embedding:在低维向量上学习表示图节点、边或者子图。思想源于特征学习和单词嵌入,第一个图嵌入学习方法是DeepWalk,它把节点看做单词并在图上随机游走,并且在它们上面使用SkipGram模型;
基于以上两种思想,GNN会在图结构上聚合信息,因此可以对输入/输出的元素及元素间的独立性进行建模。GNN还可以同时使用RNN核对图上的扩散过程进行建模。
GNN的优势
- 标准神经网络(CNN、RNN)无法解决图输入无序性,因为它们将点的特征看做是特定的输入;
- 两点之间的边代表着独立信息,在标准神经网络中,这种信息被看做是点的信息,而GNN可以通过图结构来进行传播,而不是将其看做是特征;通常而言,GNN更新隐藏节点的状态,是通过近邻节点的权值和;
- 高级人工只能需要更高的可解释性;标准神经网络可以生成合成图像或文档,但无法生成图;GNN可以生成无结构的数据(多种应用:文字分类、神经机器翻译、关系提取、图像分类);
GNN不足
- 更新节点的隐藏状态是低效的;
- 在迭代中使用相同的参数,更新节点隐藏状态是时序的;
- 在边上有一些信息化的特征无法在原始GNN中建模;如何学习边的隐藏状态也是问题;
- 如果我们的目标是节点的表示而不是图,使用固定点H是不合适的;
GNN改进&变种
对GNN的改进分为如下三种:
- 图类型改进;
- 传播步骤改进;
- 训练方法改进;
图类型
原始GNN的输入图是带有标记信息的节点和无向边。以下是几种不同的图类型:
- 有向图:信息更紧密;
- 异质图:包含几种不同的节点,最简单的处理方式是one-hot feature vector;
- 带边信息的图:每个边也有信息、权值和类型,我们可以将边也变成节点,或者当传播时在不同的边上使用不同的权重矩阵;
传播步骤
对GNN而言,传播步骤是非常重要的,它可以获得节点(边)的隐藏状态。传播步骤使用的方法通常是不同的聚合函数(在每个节点的邻居收集信息)和特定的更新函数(更新节点隐藏状态)。
卷积操作
在图上的卷积操作通常可以分为光谱方法和非光谱方法。
- 光谱方法:光谱方法在图的光谱表示上运行,学习的过滤器是基于拉普拉斯特征权重的,因此与图的结构紧密相关,难以泛化;
- 非光谱方法:直接在图上定义卷积,对紧密相近的节点进行操作,主要的挑战就是非光谱方法在不同大小的邻居上的定义和保持CNN的局部变量,非光谱方法具有点分类和图分类两种;
Gate闸门机制
在GNN中使用门限机制是为了减少限制并改善长期的图结构上的信息传递。
Attention注意力机制
注意力机制已经成功的应用于基于时序的任务,例如机器翻译、机器阅读等。GAT在传播步骤使用了注意力机制,会通过节点的邻居来计算节点的隐藏状态,通过自注意策略。
Skip connection
许多机器学习的应用都会使用多层神经网络,然而多层神经网络不一定更好,因为误差会逐层累积,最直接定位问题的方法,残差网络,是来自于计算机视觉。即使使用了残差网络,多层GCN依旧无法像2层GCN一样表现良好。
有一种方法是使用高速路GCN(Highway GCN),它像高速路网络一样使用逐层门限。
训练方法
原始的图神经网络在训练和优化步骤有缺陷,它需要完整的图拉普拉斯,对大图而言计算力消耗大。更多的,层L上的节点嵌入是递归计算的,通过嵌入它的所有L-1层的邻居。因此,单层节点是成倍增长的,因此对节点的计算消耗巨大。且GCN是对每个固定图进行独立训练的,因此泛化能力不好。
以下是几种改善方式:
- GraphSAGE:
将全图拉普拉斯替换为可学习聚合函数,是使用信息传递并生长到未见节点的关键,GraphSAGE还使用了邻居采样来避免接收域爆炸; - FastGCN:
FastGCN对采样算法做了更深的改进,FastGCN为每层直接采样接受域,而非对每个节点进行邻居采样; - control-variate based stochastic approximation:
使用节点的历史激励作为控制随机数,此方法限制接受域为1跳邻居,但使用历史隐藏状态作为可接受最优化方法; - Co-Training GCN and Self-Training GCN:
用于解决GCN需要许多额外的有标记数据及卷积过滤器的局部特征的限制,因此使用了此方法来扩大训练数据集,Co-Training方法为训练数据找到最近的邻居,Self-Training则采用了类似boosting的方法。
框架
框架的目的是集合不同的模型。有论文提出message passing neural network(MPNN),可以同一化多种图神经网络和图卷积网络方法。non-local neural network(NLNN) 则同一化了几个自注意方法。graph network(GN) 统一了MPNN和NLNN,还有其他的Interaction Networks,Neural Phsics Engine,CommNet, structure2vec,GGNN,Relation Network,Deep Sets和Point Net。
MPNN
MPNN是监督学习的框架,它抽象了几个最流行的用于处理图结构数据的模型的相似性。模型包括两个阶段,信息传递阶段和读出阶段。
- 信息传递阶段: 就是传播阶段,会运行T次。是以信息传递函数和端点更新函数为定义的。
- 读出阶段: 读出阶段会使用读出函数来对整个图计算特征向量。
NLNN
NLNN是用来对深度神经网络的长范围的独立性。non-local操作来源于经典non-local mean操作在计算机视觉上的应用。non-local操作会在一个位置上计算响应,同时加权了的特征和在所有点上。这些位置可以是空间、时间或者空间时间。因此NLNN可以看做是不同的自注意方法的统一。
一般的,non-local操作被如下定义:
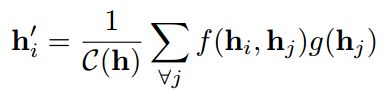
其中,i是输出位置的索引,j是指出所有可能位置的索引,f函数计算i和j之间的缩放值,这可以代表他们之间的联系,g函数代表了输入的变换以及公式的系数用于正则化结果。当使用不同的f和g函数时,将得到不同的non-local操作实例,最简单的g函数就是线性变换了。以下是一些可能选择的f函数:
- Gaussian;
- Embedded Gaussian;
- Dot product;
- Concatenation;
GN
首先是图的定义,然后是GN块,核心GN计算单元,计算步骤,最后是GN的基本设计原则。
- Graph definition: 图被定义为三元组,(全局属性,节点集合,边集合);
- GN block: GN块包括三个更新函数和三个聚合函数;
- Computation steps;
- Design Principles:
GN的设计基于三个基本原则:
flexible representation
configurable within-block structure composable multi-block
architectures
GNN的应用场景
GNN的应用场景非常多,因为GNN是应用于图信息的,而多种多样的数据都可以划分为图数据。以下是GNN的应用场景:
- 文字分类;
- 神经网络翻译;
- 关系提取;
- 图分类;
- …
在这里我们对GNN的应用进行简单的介绍,首先我们将其划分为三种场景的应用:
- 结构化场景:数据有明显的联系结构;
- 非结构化场景:联系结构不明显,例如图像、文字等;
- 其他的应用场景:生成模型、组合最优化问题等;
GNN对我的启发
GNN是对图数据进行处理的深度学习神经网络,它可以实现对异构数据的学习与表示,这里的图数据与我们通常所说的图是不一样的,这里的图指的是数据结构中的那种图以及离散数学中图论,其中不同的节点表示不同的信息。因此,图即代表实体及实体之间的联系。
在我们的日常生活中,图是无处不在的。而图结构数据具有一定的复杂性,因为图结构的数据节点通常具有是具有不同的类型的,因此相对普通的神经网络而言处理起来具有一定的难度。
GNN最重要的两点就是:1. CNN 特征提取;2. graph embedding 降维操作,再通过一些神经网络必要的训练操作等,我们就可以得到对图的大致表示。然后就可以实现分类、回归等任务了。GNN也需要防止过拟合和欠拟合,由于图数据通常过大,所以可以采用随机游走的方式,来获取图的特征。
Basic GNNs
基本思想
图神经网络的一个基本思想,就是基于节点的局部邻居信息对节点进行embedding。直观来讲,就是通过神经网络来聚合每个节点及其周围节点的信息。
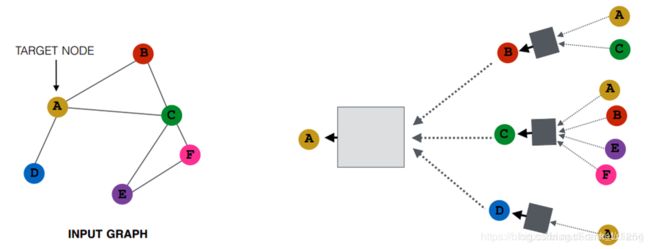
图神经网络的几个性质如下:
- 节点在每一层都会有embedding
- 模型可以达到任意深度
- 第零层的节点的embedding就是他的输入特征向量
实现
我们所要探讨的是,节点如何获取它的邻居节点的信息。最基本的想法就是聚合一个节点的邻居节点信息时,采用平均的方法,并使用神经网络作聚合操作,具体方法如下图
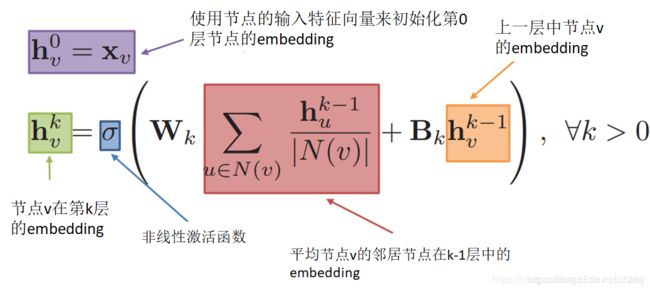
那么如何训练这个模型,具体分为监督和无监督两种方法。
无监督的方法包括:
- 随机游走(Random walks):node2vec, DeepWalk
- 图分解(Graph factorization)
- 训练模型使得相似的节点具有相似的embedding
监督的方法,以二分类举例,可以定义一个交叉熵函数来作为损失函数:
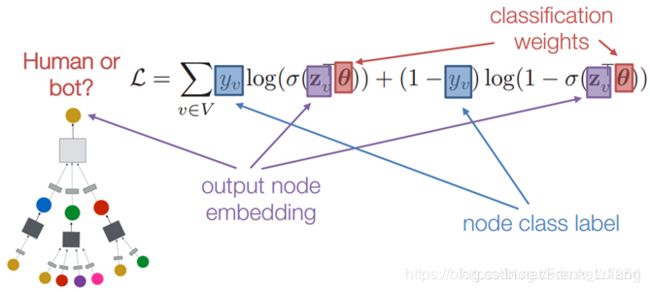
归纳性
图神经网络中每一层的聚合所使用的参数是相同的(权值共享),并且这个模型可以推理出新出现节点的embedding或者一张新图的embedding。如下图
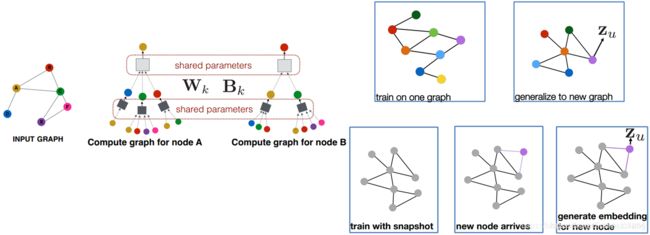
图卷积神经网络(GCN)
与基础的GNN相比,GCN只是在聚合函数上有一些细微的变化。
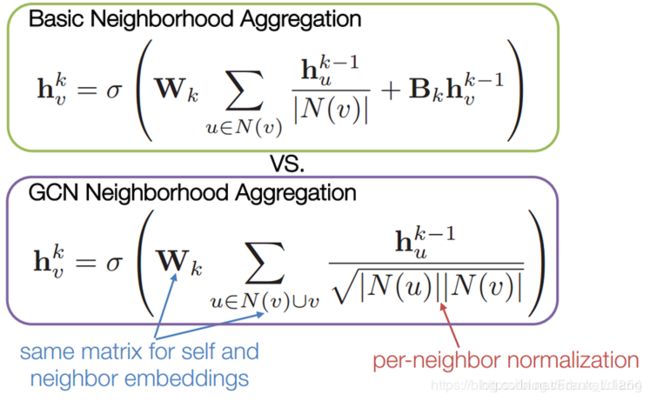
GraphSAGE
Gated Graph Neural Network
门控图神经网络主要是解决过深层的图神经网络导致过度平滑的问题,使用GRU更新节点状态。
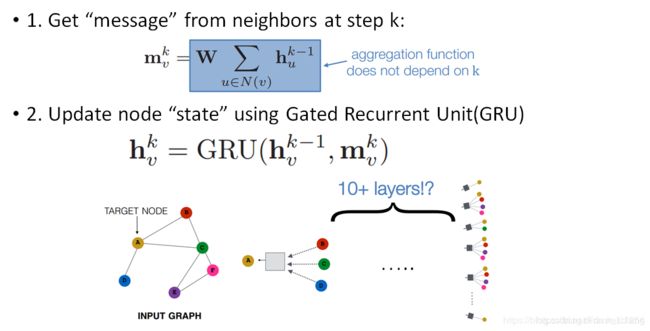
图注意力网络(Graph Attention Networks)
在基础的图神经网络上加上了注意力机制,需要去学习每个节点的注意力权重。
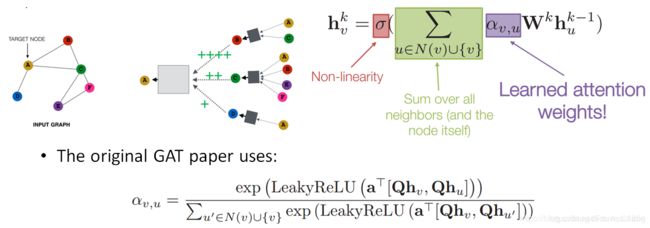
(Sub)graph Embeddings
对一个图的子图计算embedding,如下图:
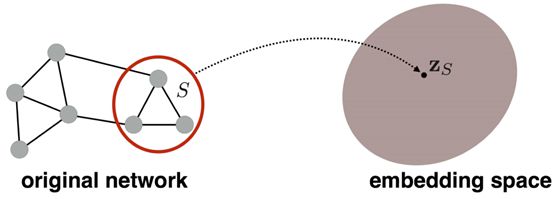
主要的方法有
- 直接加权子图中每一个节点的embedding
- 将子图当成一个虚拟节点,加入到图神经网络的计算中
- 逐层的聚合节点。
逐层聚合的步骤如下:
- 使用GNN计算节点的embedding
- 将节点聚合在一起,使得图变成一个粗粒度的图
- 在粗粒度的图上运行GNN
- 重复
Open Problems
图神经网络目前还存在很多开放性的问题需要解决
浅层结构
传统的深度学习通过叠加层数来获得更好的性能,但是图神经网络往往只有两三层,如果叠加的层数过多,会造成过度平滑,所有的节点都会收敛到一个值。
动态图
静态图是稳定的,因此可以有效建模,而当边或者节点出现或者消失的时候,GNN不能自适应变化
非结构场景
没有一种好的方法从非结构化数据中生成一张图
Scalability
时间复杂度过高,在大数据环境中很难使用。
参考地址:
https://blog.csdn.net/r1254/article/details/88343349
https://blog.csdn.net/qq_34911465/article/details/88524599
