【机器学习笔记31】傅里叶变换

【参考资料】
【1】《复变函数与积分变换》
【2】《数字信号处理》

1. 傅里叶级数

定义: 设$f_T(t)$是以T为周期的实值函数，且在$[-\frac{T}{2},\frac{T}{2}]$上满足狄利克雷条件，即：
1）连续或只有有限个第一类间断点；
备注：第一类间断点包括：
可去间断点：左右极限存在且相等，但不等于该点的值，或该点无定义；
跳跃间断点：左右极限存在但不相等
2）只有有限个极值点

那么$f_T(t)$在连续点处有

傅里叶级数的三角形式

$f_T(t)=\frac{a_0}{2}+\sum _{n=1}^{+\infty }(a_n\cos n{\omega }_{0}t+b_n\sin n{\omega }_{0}t)$
$w_0=\frac{2\pi }{T}$

$a_n=\frac{2}{T}{\int }_{-T/2}^{T/2}{f}_T(t)\cos n{\omega }_{0}tdt$其中$n=0,1,2,\dots$

$b_n=\frac{2}{T}{\int }_{-T/2}^{T/2}{f}_T(t)\sin n{\omega }_{0}tdt$其中$n=0,1,2,\dots$

傅里叶级数的复指数形式

$f_T(t)=\sum _{-\infty }^{+\infty }{c}_n{e}^{jn{\omega }_{0}t}$
$c_n=\frac{1}{T}{\int }_{-T/2}^{T/2}{f}_T(t)e^{-jn{\omega }_{0}t}dt$

---

2. 傅里叶变换

周期函数可以展开为傅里叶级数。从物理上将周期为T的函数可以由一系列${\omega }_0=\frac{2\pi }{T}$为间隔的离散频率所形成的简谐波合成。当T越来越大时，取得频率间隔越来越小，当T变成无穷大时，周期函数就变成了非周期函数，此时傅里叶级数就转变称了傅里叶变换。

推导如下:

$f(t)=\underset{T\to +\infty }{\lim }{f}_T(t)$
$=\underset{T\to +\infty }{\lim }\sum _{n=-\infty }^{n=+\infty }[\frac{1}{T}{\int }_{-T/2}^{T/2}{f}_T(\tau )e^{-jn{\omega }_0\tau }d\tau ]e^{jn{\omega }_{0}t}$

在周期函数下时域信号被分解为频率${\omega }_0=\frac{2\pi }{T}$的简谐波，此时T区域无穷。

因此有越来越小的${\omega }_0$记作$\Delta \omega$，而$n{\omega }_0$记作${\omega }_n$, 并且$T=\frac{2\pi }{\Delta \omega }$
于是有:

$f(t)=\frac{1}{2\pi }\underset{\Delta \omega \to 0}{\lim }\sum _{n=-\infty }^{n=+\infty }[{\int }_{-\pi /\Delta \omega }^{\pi /\Delta \omega }{f}_T(\tau )e^{-j{\omega }_n\tau }d\tau .e^{j{\omega }_{n}t}]\Delta \omega$

$f(t)=\frac{1}{2\pi }\underset{-\infty }{\overset{+\infty }{\int }}[\underset{-\infty }{\overset{+\infty }{\int }}f(\tau )e^{-j\omega \tau }d\tau ]e^{j\omega t}d\omega$

因此得到定理如下（傅里叶变换）：
$F(\omega )=\underset{-\infty }{\overset{+\infty }{\int }}f(t)e^{-j\omega t}dt$
$f(t)=\frac{1}{2\pi }\underset{-\infty }{\overset{+\infty }{\int }}F(\omega )e^{j\omega t}d\omega$

3. 单位冲击函数

单位冲击函数定义:
1）当$t̸=0$时，$\xi (t)=0$
2）${\int }_{-\infty }^{+\infty }\xi (t)dt=1$

主要性质：
1 当实数域有界函数f(t)，在t=0点连续，则${\int }_{-\infty }^{+\infty }\xi (t)f(t)dt=f(0)$
2 当实数域有界函数f(t)，在$t=t_0$点连续，则${\int }_{-\infty }^{+\infty }\xi (t-t_0)f(t)dt=f(t_0)$
3 $\xi (t)$是偶函数，有$\xi (t)=\xi (-t)$
4 $\xi (t)$是单位阶跃函数$\mu (t)$的导数
$\mu (t)=\{\begin{array}{ll}1,& t>0\\ 0,& t<0\end{array}$

5 $\xi (t)$函数的傅里叶变换

公式1：$F(\omega )=F[xi(t)]={\int }_{-\infty }^{+\infty }\xi (t)e^{-j\omega t}dt=e^{-jwt}{|}_{t=0}=1$
公式2：$F^{-1}[1]=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{e}^{-j\omega t}d\omega =\xi (t)$ //根据逆变换可知
根据上面两个公式，我们可以作出如下推导:
对$f(t)=1$，其傅里叶变换（由公式2） $F(\omega )={\int }_{-\infty }^{+\infty }{e}^{-j\omega t}dt=2\pi \xi (t)$
对$f(t)=e^{j{\omega }_{0}t}$
$F(\omega )={\int }_{-\infty }^{+\infty }{e}^{j{\omega }_{0}t}{e}^{-j\omega t}dt=2\pi \xi ({\omega }_0-\omega )$
对$f(t)=cos{\omega }_{0}t=1/2{\int }_{-\infty }^{+\infty }(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t})e^{-j\omega t}dt=\pi [\xi (\omega -{\omega }_0)+\xi (\omega +{\omega }_0)]$

因此在广义的傅里叶变换下周期函数仍然可以以傅里叶变换展开

4. 离散傅里叶变换

设x(n)是一个长度为M的有限长序列，则定义x(n)的N点离散傅里叶变换为:
$X(k)=DFT[x(n)]=\sum _{n=0}^{N-1}{W}_N^{kn}k=0,1,2,\dots ,N-1$

X(k)的傅里叶逆变换为:
$x(n)=IDFT[X(k)]=\frac{1}{N}\sum _{n=0}^{N-1}X(k)W_N^{-kn}n=0,1,2,\dots ,N-1$
其中$W_N=e^{-j\frac{2\pi }{N}}$，N是DFT变换区间长度，$N\ge M$

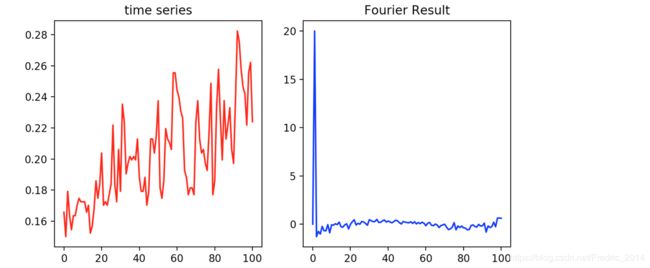
5. 代码实现(numpy和纯python)

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import matplotlib.ticker as tik
import pandas as pd
import numpy as np
import math


def _fft_code():

    plt.figure(figsize=(8, 4))

    df = pd.read_csv('./data/test.csv', sep=',')

    data = df['std_value'].astype(float)

    ax1 = plt.subplot(1,2,1)
    ax1.set_title('time series')
    plt.gca().yaxis.set_major_formatter(tik.FormatStrFormatter('%1.2f'))

    plt.plot(data,'r')

    list_len = len(data)

    y = data

    m = np.floor(list_len) #DFT中的N,要求N >= M，这里字节用序列长度

    a = np.zeros(int(m))
    b = np.zeros(int(m))
    c = np.zeros(int(m))

    N = int(list_len - 1)

    for i in range(0, int(m)- 1):
       for t in range(0, N - 1):

           a[i + 1] = a[i + 1] + y[t + 1] * np.cos(2 * np.pi * i * t/N)
           b[i + 1] = b[i + 1] + y[t + 1] * np.sin(2 * np.pi * i * t/N)

       c[i + 1] = a[i + 1] + b[i + 1]

    ax2 = plt.subplot(1,2,2)
    ax2.set_title('Fourier Result')
    plt.plot(c,'b')
    plt.show()


def _fft_np():

    df = pd.read_csv('./data/test.csv', sep=',')

    data = df['std_value']

    fig = plt.figure(figsize=(8, 4))

    

    ax1 = plt.subplot(1,2,1)
    ax1.set_title('time series')
    plt.gca().yaxis.set_major_formatter(tik.FormatStrFormatter('%1.2f'))


    plt.plot(data,'r')

    transformed = np.fft.fft(data)

    d = abs(transformed) 
    x = np.arange(len(d))

    ax2 = plt.subplot(1,2,2)
    ax2.set_title('Fourier Result')
    plt.plot(d,'b')

    plt.show()

"""
说明：

傅里叶变换代码实现，对应的笔记《傅里叶变换》

作者：fredric

日期：2018-11-18

_fft_np: 采用numpy自带傅里叶变换函数

_fft_code: 纯python代码，依据基本的DFT推导，未采用FFT


"""

if __name__ == '__main__':

    _fft_code()

    _fft_np()