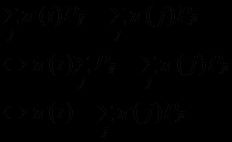马尔科夫蒙特卡洛算法(MCMC)

趁着周末，学习了此算法。一个重要的作用就是用来模拟目标分布的样本。下面看看具体情况。

---

1.名词解释
MCMC方法就是*构造合适的马尔科夫链进行抽样而使用蒙特卡洛方法进行积分计算,既然马尔科夫链可以收敛到平稳分布。我们可以建立一个以π为平稳分布的马尔科夫链，对这个链运行足够长时间之后，可以达到平稳状态。此时马尔科夫链的值就相当于在分布π(x)中抽取样本。利用马尔科夫链进行随机模拟的方法就是MCMC。

第一个MC: Monte Carlo(蒙特卡洛)。这个简单来说是让我们使用随机数（随机抽样）来解决计算问题。在MCMC中意味着：后验分布作为一个随机样本生成器，我们利用它来生成样本(simulation)，然后通过这些样本对一些感兴趣的计算问题（特征数，预测）进行估计。

第二个MC：Markov Chain(马尔科夫链)。第二个MC是这个方法的关键，因为我们在第一个MC中看到，我们需要利用后验分布生成随机样本，但后验分布太复杂，当这些样本独立时，利用大数定律样本均值会收敛到期望值。如果得到的样本是不独立的，那么就要借助于马尔科夫链进行抽样，利用Markov Chain的平稳分布这个概念实现对复杂后验分布的抽样。

2.马尔科夫链的定义如下：
设θ(t)是一个随机过程，如果它满足下面的性质：
p(θ(t+h)=xt+h|θ(s)=xs,s≤t)=p(θ(t+h)=xt+h|θ(t)=xt), 任意的h>0。

这个定义又称为马尔科夫性质，对一个马尔科夫链来说，未来状态只与当前t时刻有关，而与t时刻之前的历史状态无关（条件独立）。

马尔科夫链的一个很重要的性质是平稳分布。简单的说，主要统计性质不随时间而变的马尔科夫链就可以认为是平稳的。数学上有马氏链收敛定理，当步长n足够大时，一个非周期且任意状态联通的马氏链可以收敛到一个平稳分布π(x)。这个定理就是所有的MCMC方法的理论基础。

结论：一个Markov链可以由它的初始状态以及转移概率矩阵P完全确定。

3.什么是平稳分布？它和求极限概率分布有什么关系呢？

定义：Markov链有转移概率矩阵P，如果有一个概率分布{πi}满足,则称为这个Markov链的平稳分布。这个定义用矩阵形式写出来就是π*P=π.

 这个定义的含义：如果一个过程的初始状态X0有平稳分布π,我们可以知道对所有n，Xn有相同的分布π。再根据Markov性质可以得到，对任何k，有
 Xn,Xn+1,...,Xn+k的联合分布不依赖于n，显然这个过程是严格平稳的，平稳分布也由此得名！！

4.拒绝抽样

基本思想是，我们需要对一个分布f(x)进行采样，但是却很难直接进行采样，所以我们想通过另外一个容易采样的分布g(x)的样本，
用某种机制去除掉一些样本，从而使得剩下的样本就是来自与所求分布f(x)的样本。

具体的采样过程如下：

1. 对于g(x)进行采样得到一个样本xi, xi ~ g(x);
2. 对于均匀分布采样 ui ~ U(a,b);
3. 如果ui<= f(x)/[M*g(x)], 那么认为xi是有效的样本；否则舍弃该样本； （# 这个步骤充分体现了这个方法的名字：接受-拒绝）
4. 反复重复步骤1~3，直到所需样本达到要求为止。

示例：产生服从beta(2,7)的随机数。提议分布g取为均匀分布,常数M取为beta(2,7)的密度函数的最大值。

a <- 2
b <- 7
xmax <- (a-1)/(a+b-2)
dmax <- xmax^(a-1)*(1-xmax)^(b-1)*gamma(a+b)/(gamma(a)*gamma(b))
y <- runif(1000)
x <- na.omit(ifelse(runif(1000) <= dbeta(y,a,b)/dmax,y,NA))

查看ks检验:

z <- x[1:323]
ks.test(z,"pbeta",2,7)
#接受域图
plot(dbeta(x,2,7)~x,type = "l")

5.M-H抽样

可逆马氏链的可逆性经常表示为(细致平衡方程,detailed balance equations) ,从而如果一个目标分布满足此细致平衡方程，则容易验证

根据 平稳分布的定义。

MH算法：
下面按如下方式定义一个马氏链：
1.从时刻t的状态i转移到下个时刻的状态，由转移核生成一个候选的状态j；
2.以概率min{1,pj/pi}接受下一时刻的状态为Xt+1=j,否则Xt+1=i
这里用到了马尔科夫链的另一个性质，如果具有转移矩阵P和分布π(x)的马氏链对所有的状态i,j满足下面的等式：π(i)p(i,j)=π(j)p(j,i)
这个等式称为细致平衡方程。满足细致平衡方程的分布π(x)是平稳的。 所以我们希望抽样的马尔科夫链是平稳的，可以把细致平衡方程作为出发点。
示例：
使用MH抽样法,从Rayleigh分布中抽样,Rayleigh分布的密度为：
，取自由度为Xt的卡方分布为提议分布，则使用MH算法如下：
1). 令g(.|x)为X2(df=x)
2).从X2(1)中产生X0，并存在X[1]中。
3). 对i=2,….,N，重复,
(a) 产生备选样本,从X2(df=Xt)=X2(df=X[i-1])中产生Y
(b) 产生U~U(0,1)
(c)在Xt=X[i-1]，计算
若U <= r(Xt,Y ),则接受Y,令Xt+1 =Y,否则令Xt+1=Xt

例如：
利用M-H抽样方法从Rayleigh分布中抽样，此分布的密度函数为：

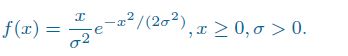
# 计算Rayleigh密度函数在某点的值
f <- function(x,s)
{
  if(x < 0)  return (0)
  stopifnot(s > 0) # if not all true,stop is called
  return((x/s^2)*exp(-x^2/(2*s^2)))
}

N <- 10000
s <- 4
x <- numeric(N)
x[1] <- rchisq(1,df=1) #初始化提议分布
k <- 0
u <- runif(N)
for(i in 2:N)
{
  y <- rchisq(1,df = x[i-1]) #候选点
  num <- f(y,s)*dchisq(x[i-1],df = y) 
  den <- f(x[i-1],s)*dchisq(y,df = x[i-1])
  if (u[i] <= num/den) 
    x[i] <- y
  else {
    x[i] <- x[i-1]
    k <- k+1 #y is rejected
  }  
}
print(k)

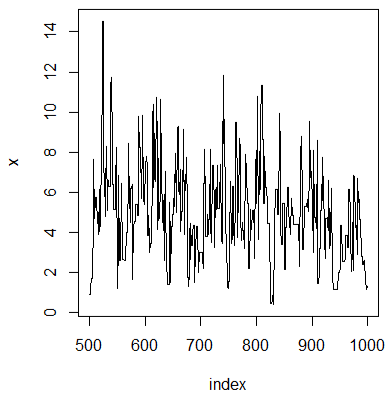
# 做样本路径图(trace plot)
index <- 500:1000
y1 <- x[index]
plot(index,y1,type = "l",main = "",ylab = "x")
 #在候选点被拒绝的时间点上链没有移动,因此图中有很多短的水平平移

stopifnot()对函数参数进行检验，可看帮助文档

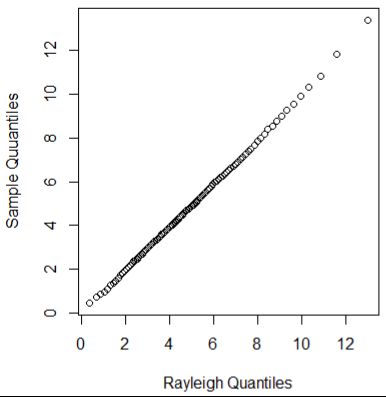
接下来比较Rayleigh分布的分位数和MH算法下得到样本分位数

b <- 2001 # discard the burnin(2000个) sample
y <- x[b:N]
a <- ppoints(100) #产生概率点,用来计算分位点
QR <- s*sqrt(-2*log(1-a)) # quantiles of Rayleigh
Q <- quantile(x,a)  #quantitles of MH
qqplot(QR,Q,main = "",xlab = "Rayleigh Quantiles",
       ylab = "Sample Quuantiles")
hist(y,breaks = "scott",main = "",xlab = "",freq = FALSE)
lines(QR,f(QR,4))

6.随机游动的MH算法

使用提议分布N(Xt,s^2)和随机游动Metropolis算法产生自由度为V的t分布随机数

rw.Metropolis <- function(n,sigma,x0,N){
  # n: degree of freedom of t distribution
  # sigma: standard variance of proposal distribution  N(xt,sigma)
  # x0: initial value
  # N: size of random numbers required.
  x <- numeric(N)
  x[1] <- x0
  u <- runif(N)
  k <- 0
  for(i in 2:N)
  {
    y <- rnorm(1, x[i-1], sigma)
    if(u[i] <= dt(y,n)/dt(x[i-1],n))
      x[i] <- y
    else{
      x[i] <- x[i-1]
      k <- k+1
    }
  }
  return (list(x=x,k=k))
}

n <- 4
N <- 2000
sigma <- c(.05,.5,2,16)
x0 <- 25
rw1 <- rw.Metropolis(n,sigma[1],x0,N)
rw2 <- rw.Metropolis(n,sigma[2],x0,N)
rw3 <- rw.Metropolis(n,sigma[3],x0,N)
rw4 <- rw.Metropolis(n,sigma[4],x0,N)

# rate of candidate points rejected
print(c(rw1$k,rw2$k,rw3$k,rw4$k)/N)

拒绝率

[1] 0.0040 0.1220 0.4645 0.9085

只有第二个链的拒绝率在区间[0.15,0.5]
在不同的提议分布方差下,检验所得链的收敛性

par(mfrow=c(2,2))
refline <- qt(c(0.25,0.975),df=n)
rw <- cbind(rw1$x,rw2$x,rw3$x,rw4$x)
for(j in 1:4){
  plot(rw[,j],type = "l", #trace plot
       xlab = bquote(sigma==.(round(sigma[j],3))),
       ylab = "x",
       ylim = range(rw[,j]))

  abline(h = refline)
}
par(mfrow=c(1,1)) # reset to default

路径图

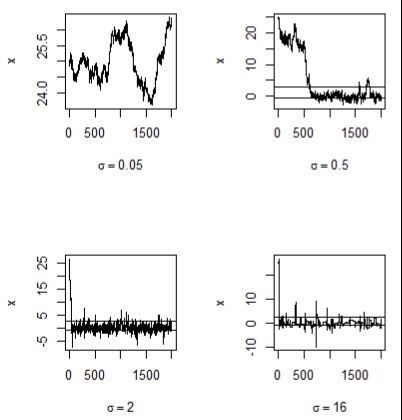
可以看出,sigma^2=0.05时,增量太小，几乎每个候选点都被接受了，链在2000次迭代后还没有收敛。
Sigma^2=0.5,链的收敛较慢;sigma^2=2时，链很快收敛；而sigma^2=16时，接受的概率太小，使得大部分候选点都被拒绝了(图形放大看,有很多小区间-)。

bquote(expr) #引用表达式,其中封装在.()中的要被计算出来

7.Gibbs抽样

可以看做MH算法当alpha=1的一个特例,用于目标分布为多元分布的情况。

假设在多元分布中所有的一元条件分布都是可以确定的,记m维随机向量X=(X1,X2,…,Xm)`
X-i表示X中去掉分量Xi后剩余的m-1维向量,那么一元条件分布就是f(xi|x-i)

Gibbs抽样就是在这m个条件分布中迭代产生样本，算法：
1)给出初值X(0);
2)对t=1,…,T进行迭代

• (a)令x1=X1(t−1)；
• (b)依次更新每一个分量，即对i=1,…,m,
  (i)从f(Xi∣X−i(t−1))中产生抽样Xi(t)；
  (ii)更新xi(t)=Xi(t)；
• (c)令X(t)=(X1(T),X2(T),…,Xm(T))′(每个抽取的样本都被接受了)；
• (d)更新t。
  在这个算法里，对每一个状态t,X(t)的分量是依次更新的。这个分量更新的过程是在一元分布f(Xi∣X−i)中进行的，所以抽样是比较容易的。

示例：使用Gibbs抽样抽取二元正态分布N(μ1,μ2,σ12,σ22,ρ)的随机数 在二元正态分布的条件下，两个分量的一元条件分布依然是正态分布：
f(x1∣x2)∼N(μ1+ρσ1σ2(x2−μ2),(1−ρ2)σ12)
f(x2∣x1)∼N(μ2+ρσ2σ1(x1−μ1),(1−ρ2)σ22)

p_ygivenx <- function(x,m1,m2,s1,s2)
{
  return(rnorm(1,m2+rho*s2/s1*(x-m1),sqrt(1-rho^2)*s2))
}
p_xgiveny <- function(y,m1,m2,s1,s2)
{
  return (rnorm(1,m1+rho*s1/s2*(y-m2),sqrt(1-rho^2)*s1))
}

N = 5000
K = 20 # iteration in each sampling
x_res = vector(length = N)
y_res = vector(length = N)
m1 = 10; m2 = -5;s1 = 5;s2 = 2
rho = 0.5
y = m2

for(i in 1:N) #采样N次
{   

   for(j in 1:k) # 每次采样迭代20次
   {
    x = p_xgiveny(y,m1,m2,s1,s2)
    y = p_ygivenx(x,m1,m2,s1,s2)
   }

    #print(x)
    x_res[i] = x;
    y_res[i] = y;
}

hist(x_res,freq = F)
dev.new()

library(MASS)
valid_range = seq(from = N/2,to = N,by = 1)
MVN.kdensity <- kde2d(x_res[valid_range],y_res[valid_range],h = 10)
plot(x_res[valid_range],y_res[valid_range],col = "blue",xlab = "x",ylab = "y")
contour(MVN.kdensity,add = TRUE)#二元正态分布等高线图  

8.关于链的收敛有这样一些检验方法。

（1）图形方法 这是简单直观的方法。我们可以利用这样一些图形：
（a）迹图（trace plot）：将所产生的样本对迭代次数作图，生成马氏链的一条样本路径。如果当t足够大时，路径表现出稳定性没有明显的周期和趋势，就可以认为是收敛了。
(b)自相关图（Autocorrelation plot）：如果产生的样本序列自相关程度很高，用迹图检验的效果会比较差。一般自相关随迭代步长的增加而减小，如果没有表现出这种现象，说明链的收敛性有问题。
（c）遍历均值图（ergodic mean plot）：MCMC的理论基础是马尔科夫链的遍历定理。因此可以用累积均值对迭代步骤作图，观察遍历均值是否收敛。
其它还有 （2）蒙特卡洛误差 （3）Gelman-Rubin方法

参考1
参考2