Java数据结构和算法之归并排序
正如我们所知,我们在学习数据结构和算法的时候必然逃不过有关于数组的排序方法,我们应该掌握的方法或许有很多,但是最基本或者说被公认为的八大排序是我们在不具备设计算法和更改算法的情况下应该去学习掌握的。在很久以前已经学习过用C语言进行实现,但是现在准备从事关于Java的工作,所以需要实践起来,用java进行实现。学习的基础都是在努自己动手的实践。
今天实现归并排序,因为我对这个排序方法却是情有独钟,作为我博客开通的第一篇文章。归并排序的核心思想在于分割数组进行递归,然后对数组进行整合排序,这样的好处在于能够节约更多的运算时间,这里就涉及到了时间复杂度和空间复杂度,归并排序的时间复杂度是说实话,学习算法这是绕不过去的门槛,但是在这里我就不多介绍了,等着实现完成在进行解析,或许怎么实现归并排序才是最关心的问题,如果掌握了其他比如冒泡排序的手段可以试一下在五十万条数据情况下它俩消费的时间。
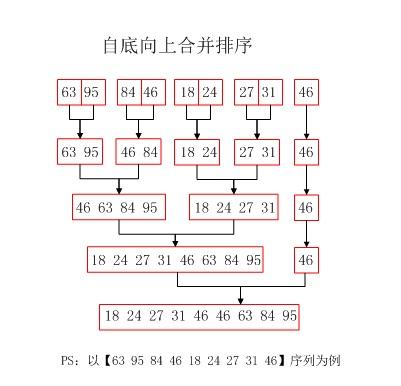
首先我们需要做的第一步就是对数组进行分割,递归分隔,直到每一个进行整合的数据都为最小单元为止。话不多说,直接上图以及实现代码。
![]()
public static void mergeSort(int arr[],int emp[],int start,int end){
//arr数组是你需要进行分割或者说是进行排序的数组
//emp是我们在进行排序整合过程中的临时数组,因为不想创建太多的临时数组耗费空间,所以用一个和排序数组等大的数组使用
//start和end是需要排序的数组或者说分隔以后数组片段的开始以及结束
//首先我们计算出中间值
int middle = (start + end) / 2;
//这个条件判断是用于限制递归的出口
if(start < end){
mergeSort(arr,emp,start,middle) // 整体数组的左边片段进行递归切割排序
mergeSort(arr,start,middle+1,end) //整体数组的右边片段进行切割排序
//调用数组整合方法,对已经切割的数组进行整合并且排序
megerArray(arr,emp,start,middle,end);
}
}
通过以上步骤我们就能把一个比较大的数据量分割成无数的单元数据,然后我们会用到一个非常重要的思想就是分而治之。对这些小的数据进行整合排序。我们需要操作的效果图如下,以及实现的代码。
public static void mergeArray(int arr[],int emp[].int start,int middle,int end){
int i = start,j = middle;
int k = middle + 1,int z = end;
int x = 0;
//这个条件用于控制是否继续进行往临时数组里面填入数据
while(i <= j&& k <= z){
//这里很关键,判断两个单元谁大谁小,小的进入临时数组,然后小的一组角标加一,继续和大的一组进行比较
if(arr[i] < arr[j]){
emp[x++] = arr[i++];
}else{
emp[x++] = arr[k++];
}
}
//经过第一轮的填入必然是左右的两个单元一个已经全部进入临时数组,一个还剩余一定,那么这时候我们需要对剩下的数据进行处理
while(i <= j){
emp[x++] = arr[i++];
}
while(k <= z){
emp[x++] = arr[k++];
}
//这时候所有的需要排列的数据必然已进入临时数组我们取出即可
for(i = 0;i < x;i++){
//这里为什么会用到start,因为我们知道我们在对两个单元进行操作的时候,我们并不知道这两个单元的开始在哪,只有通过start进行记录。比如我们在对原始数组的右半部数据进行操作时自然不能让角标从0开始,这就是使用start的意义
arr[start + i] = emp[i];
}
}
这时整个归并排序已经实现完成,它的原理图如下
![]()
通过以上的实现我们可以知道归并排序其实就是分而治之的思想进行实现,利用递归的手段进行操作,或许我们在学习归并排序的时候一定要牢记画图理解,特别是在进行递归的时候。最后我们还需要知道的是归并排序它的时间复杂度是:O拆分数组的(N log N) 主要需要考虑在拆分数组的递归以及合并的循环
公式是T[n] = 2T[n / 2] + O(n);