我钟爱的数据结构大复习
https://visualgo.net/
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
闲着无聊可以来个自测
https://pta.patest.cn/pta/test
1.好久不用C语言补充一下基础语法
#include
#include
int main()
{
int n,m,i,j,t;
char sign;
scanf("%d %c",&n,&sign);
n-=1;
m=1;/*开始必有一行是一个点的*/
while(n-2*(m+2)>=0)
{
m+=2;
n-=2*m;
}
t=m/2;
for(i=0;ifor(j=0;jabs(i-t);j++)
printf(" ");
for(j=0;j<abs(i-t)*2+1;j++)
printf("%c",sign);
printf("\n");
}
printf("%d\n",n);
return 0;
} 2.1 线性表的顺序表示和实现
Common.h
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status; SqList.h
//------线性表的动态分配顺序存储结构--------
#include
#include "Common.h"
#define ElemType int
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
ElemType* elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
} SqList;
//基本操作
Status InitList(SqList &L);
//操作结果:构造一个空的线性表L。
Status DestroyList(SqList &L);
//初始条件:线性表L已存在。
//操作结果:销毁线性表L。
Status ClearList(SqList &L);
//初始条件:线性表L已存在。
//操作结果:将L重置为空表。
bool ListEmpty(SqList L);
//初始条件:线性表L已存在。
//操作结果:若L为空表,则返回TRUE,否则返回FALSE。
int ListLength(SqList L);
//初始条件:线性表L已存在。
//操作结果:返回L中数据元素的个数。
Status GetElem(SqList L, int i, ElemType &e);
//初始条件:线性表L已存在,1<=i<=ListLength(L)。
//操作结果:用e返回L中第i个数据元素的值。
int LocateElem(SqList L, int e, bool (*equal)(ElemType, ElemType));
//初始条件:线性表L已存在,compare()是数据元素判定函数。
//返回L中第一个与e满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回值为0.
Status PriorElem(SqList L, ElemType cur_e, ElemType &pre_e);
//初始条件:线性表L已存在。
//操作结果:若cur_e是L中的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义。
Status NextElem(SqList L, ElemType cur_e, ElemType &next_e);
//初始条件:线性表L已存在。
//操作结果:若cur_e是L中的数据元素,且不是最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义。
Status ListInsert(SqList &L, int i, ElemType e);
//初始条件:线性表L已存在,1<=i<=ListLength(L)+1.
//操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1.
Status ListDelete(SqList &L, int i, ElemType &e);
//初始条件:线性表L已存在且非空,1<=i<=ListLength(L).
//操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1.
Status ListTraverse(SqList L, bool (*visit)(ElemType));
//初始条件:线性表L已存在
//操作结果:依次对L的每个元素调用函数visit().一旦visit()失败,则操作失败。 SqList.cpp
#include
#include "SqList.h"
Status InitList(SqList &L){
//操作结果:构造一个空的线性表L。
L.elem = (ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType));
if(!L.elem) exit(OVERFLOW); //存储分配失败
L.length = 0;
L.listsize = LIST_INIT_SIZE;
return OK;
}//InitList
Status DestroyList(SqList &L){
//操作结果:销毁线性表L。
// free(&L);
free(L.elem)
return OK;
}
Status ClearList(SqList &L) {
//操作结果:将L重置为空表。
L.length = 0;
return OK;
}
bool ListEmpty(SqList L){
//操作结果:若L为空表,则返回TRUE,否则返回FALSE。
if(0 == L.length)
return true;
else return false;
}
int ListLength(SqList L){
//操作结果:返回L中数据元素的个数。
return L.length;
}
Status GetElem(SqList L, int i, ElemType &e){
//1<=i<=ListLength(L)。
//操作结果:用e返回L中第i个数据元素的值。
if(i < 1 || i>=L.length) return ERROR;
e = L.elem[i-1];
return OK;
}
int LocateElem(SqList L, ElemType e, bool (*equal)(ElemType, ElemType)){
//compare()是数据元素判定函数。
//返回L中第一个与e满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回值为0.
int i = 1;
ElemType* p = L.elem;
while(i <= L.length && !(*equal)(*p++, e)) ++i;
if(i <= L.length) return i;
else return 0;
}
Status PriorElem(SqList L, ElemType cur_e, ElemType &pre_e){
//操作结果:若cur_e是L中的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义。
int i=1;
while(i <= L.length && !(cur_e==L.elem[i-1])) ++i;
if(i<2 || i>L.length)
return ERROR;
pre_e = L.elem[i-2];
return OK;
}
Status NextElem(SqList L, ElemType cur_e, ElemType &next_e){
//操作结果:若cur_e是L中的数据元素,且不是最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义。
int i=1;
while(i <= L.length && !(cur_e==L.elem[i-1])) ++i;
if(i<2 || i>L.length)
return ERROR;
next_e = L.elem[i];
return OK;
}
Status ListInsert(SqList &L, int i, ElemType e){
//1<=i<=ListLength(L)+1.
//操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1.
if(i < 1 || i>L.length+1) return ERROR; //i值不合法
if(L.length >= L.listsize) {
ElemType * newbase = (ElemType *)realloc(L.elem, (L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(!newbase) exit(OVERFLOW);
L.elem = newbase;
L.listsize += LISTINCREMENT;
}
ElemType * q = &(L.elem[i-1]); //q为插入位置
ElemType * p;
for(p=&(L.elem[L.length-1]);p>=q;--p)
*(p+1) = *p; //右移
*q = e;
++L.length;
return OK;
}//ListInsert
Status ListDelete(SqList &L, int i, ElemType &e){
//1<=i<=ListLength(L).
//操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1.
if(i<1 || i>L.length) return ERROR;
ElemType* p = &(L.elem[i-1]);
e = *p;
ElemType* q = L.elem + L.length - 1;
for(++p;p<=q;++p) *(p-1) = *p;
--L.length;
return OK;
}
Status ListTraverse(SqList L, bool (*visit)(ElemType)){
//操作结果:依次对L的每个元素调用函数visit().一旦visit()失败,则操作失败。
int i=1;
ElemType* p = L.elem;
while(i <= L.length && (*visit)(*p++)) ++i;
return OK;
} main.cpp
#include
#include "SqList.h"
bool equal(int a, int b){
if(a == b)
return true;
return false;
}
bool visit(ElemType e){
printf(" %d", e);
return true;
}
int main()
{
SqList L;
ElemType e;
ElemType pre_e;
ElemType next_e;
InitList(L);
if(ListEmpty(L))
printf("kong\n");
for(int i=0;i<30;i++){
e = i+1;
ListInsert(L, i+1, e);
}
e = 15;
printf("15所在的位置为: %d\n", LocateElem(L, 15, equal));
PriorElem(L, e, pre_e);
NextElem(L, e, next_e);
printf("e的前驱为:%d\n", pre_e);
printf("e的后驱为:%d\n", next_e);
GetElem(L, 22, e);
printf("第22个数为:%d\n", e);
printf("遍历:");
ListTraverse(L, visit);
printf("\n");
printf("List length is:%d\n", ListLength(L));
ClearList(L);
printf("清空\n");
printf("List length is:%d\n", ListLength(L));
if(ListEmpty(L))
printf("kong\n");
ListInsert(L, 1, 3);
ListInsert(L, 2, 7);
ListInsert(L, 3, 9);
ListInsert(L, 4, 1);
ListInsert(L, 5, 44);
printf("List length is:%d\n", ListLength(L));
printf("遍历:");
ListTraverse(L, visit);
printf("\n");
ListDelete(L, 3, e);
printf("所删除的值为: %d\n", e);
printf("遍历:");
ListTraverse(L, visit);
printf("\n");
printf("xiaohui:\n");
DestroyList(L);
system("pause");
return 0;
} 2.2 堆栈
定义:堆栈是一个在计算机科学中经常使用的抽象数据类型。堆栈中的物体具有一个特性: 最后一个放入堆栈中的物体总是被最先拿出来, 这个特性通常称为后进先出(LIFO)队列。 堆栈中定义了一些操作。 两个最重要的是PUSH和POP。 PUSH操作在堆栈的顶部加入一 个元素。POP操作相反, 在堆栈顶部移去一个元素, 并将堆栈的大小减一。
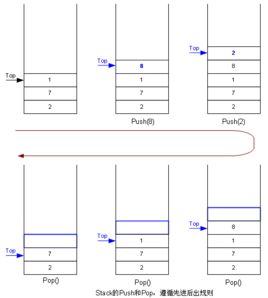
详细理论知识百度百科“堆栈”
2.3 队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素成为出队。因为队列只允许在一段插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除,故队列又称为先进先出(FIFO—first in first out)线性表。[1]
(1)初始化队列:Init_Queue(q) ,初始条件:队q 不存在。操作结果:构造了一个空队;
(2)入队操作: In_Queue(q,x),初始条件: 队q 存在。操作结果: 对已存在的队列q,插入一个元素x 到队尾,队发生变化;
(3)出队操作: Out_Queue(q,x),初始条件: 队q 存在且非空,操作结果: 删除队首元素,并返回其值,队发生变化;
(4)读队头元素:Front_Queue(q,x),初始条件: 队q 存在且非空,操作结果: 读队头元素,并返回其值,队不变;
(5)判队空操作:Empty_Queue(q),初始条件: 队q 存在,操作结果: 若q 为空队则返回为1,否则返回为0。
在STL中,对队列的使用很是较完美
下面给出循环队列的运算算法:
(1)将循环队列置为空
//将队列初始化
SeQueue::SeQueue()
{ front=0;
rear=0;
cout<<"init!"<2)判断循环队列是否为空
int SeQueue::Empty()
{ if(rear==front) return(1);
else return(0);
}
(3)在循环队列中插入新的元素x
void SeQueue::AddQ(ElemType x)
{ if((rear+1) % MAXSIZE==front) cout<<" QUEUE IS FULL! "<else{ rear=(rear+1) % MAXSIZE;
elem[rear]=x;
cout<<" OK!";
}
}
(4)删除队列中队首元素
ElemType SeQueue::DelQ()
{ if(front==rear)
{ cout<<" QUEUE IS EMPTY! "<return -1;}
else{ front=(front+1) % MAXSIZE;
return(elem[front]);
}
}
(5)取队列中的队首元素
ElemType SeQueue::Front()
{ ElemType x;
if(front== rear)
cout<<"QUEUE IS EMPTY "<else x= elem[(front+1)%MAXSIZE];
return (x);
} 详细理论知识和方法同 百度百科“队列”
http://www.cnblogs.com/kaituorensheng/archive/2013/02/28/2937865.html同参考
3.1 树与树的表示
父节点表示法
存储结勾
/* 树节点的定义 */
#define MAX_TREE_SIZE 100
typedef struct{
TElemType data;
int parent; /* 父节点位置域 */
} PTNode;
typedef struct{
PTNode nodes[MAX_TREE_SIZE];
int n; /* 节点数 */
} PTree;基本操作
设已有链队列类型LinkQueue的定义及基本操作(参见队列)。
构造空树
清空或销毁一个树也是同样的操作
void ClearTree(PTree *T){
T->n = 0;
}构造树
void CreateTree(PTree *T){
LinkQueue q;
QElemType p,qq;
int i=1,j,l;
char c[MAX_TREE_SIZE]; /* 临时存放孩子节点数组 */
InitQueue(&q); /* 初始化队列 */
printf("请输入根节点(字符型,空格为空): ");
scanf("%c%*c",&T->nodes[0].data); /* 根节点序号为0,%*c吃掉回车符 */
if(T->nodes[0].data!=Nil) /* 非空树 */ {
T->nodes[0].parent=-1; /* 根节点无父节点 */
qq.name=T->nodes[0].data;
qq.num=0;
EnQueue(&q,qq); /* 入队此节点 */
while(i/* 数组未满且队不空 */ {
DeQueue(&q,&qq); /* 节点加入队列 */
printf("请按长幼顺序输入节点%c的所有孩子: ",qq.name);
gets(c);
l=strlen(c);
for(j=0;jnodes[i].data=c[j];
T->nodes[i].parent=qq.num;
p.name=c[j];
p.num=i;
EnQueue(&q,p); /* 入队此节点 */
i++;
}
}
if(i>MAX_TREE_SIZE){
printf("节点数超过数组容量\n");
exit(OVERFLOW);
}
T->n=i;
}
else
T->n=0;
} 判断树是否为空
Status TreeEmpty(PTree *T){
/* 初始条件:树T存在。操作结果:若T为空树,则返回TRUE,否则返回FALSE */
return T->n==0;
}获取树的深度
int TreeDepth(PTree *T){
/* 初始条件:树T存在。操作结果:返回T的深度 */
int k,m,def,max=0;
for(k=0;kn;++k){
def=1; /* 初始化本节点的深度 */
m=T->nodes[k].parent;
while(m!=-1){
m=T->nodes[m].parent;
def++;
}
if(maxmax=def;
}
return max; /* 最大深度 */
}
获取根节点
TElemType Root(PTree *T){
/* 初始条件:树T存在。操作结果:返回T的根 */
int i;
for(i=0;i<T->n;i++)
if(T->nodes[i].parent<0)
return T->nodes[i].data;
return Nil;
}获取第i个节点的值
TElemType Value(PTree *T,int i){
/* 初始条件:树T存在,i是树T中节点的序号。操作结果:返回第i个节点的值 */
if(i<T->n)
return T->nodes[i].data;
else
return Nil;
}
改变节点的值
Status Assign(PTree *T,TElemType cur_e,TElemType value)
{ /* 初始条件:树T存在,cur_e是树T中节点的值。操作结果:改cur_e为value */
int j;
for(j=0;j<T->n;j++)
{
if(T->nodes[j].data==cur_e)
T->nodes[j].data=value;
}
return ERROR;
}获取节点的父节点
TElemType Parent(PTree *T,TElemType cur_e){
/* 初始条件:树T存在,cur_e是T中某个节点 */ /* 操作结果:若cur_e是T的非根节点,则返回它的父节点,否则函数值为"空"*/
int j;
for(j=1;j<T->n;j++) /* 根节点序号为0 */
if(T->nodes[j].data==cur_e)
return T->nodes[T->nodes[j].parent].data;
return Nil;
}获取节点的最左孩子节点
TElemType LeftChild(PTree *T,TElemType cur_e){
/* 初始条件:树T存在,cur_e是T中某个节点 */ /* 操作结果:若cur_e是T的非叶子节点,则返回它的最左孩子,否则返回"空"*/
int i,j;
for(i=0;i<T->n;i++)
/* 找到cur_e,其序号为i */
break;
/* 根据树的构造函数,孩子的序号>其父节点的序号 */ if(T->nodes[j].parent==i)
/* 根据树的构造函数,最左孩子(长子)的序号<其它孩子的序号 */
return T->nodes[j].data;
return Nil;
}
获取节点的右兄弟节点
TElemType RightSibling(PTree *T,TElemType cur_e){
/* 初始条件:树T存在,cur_e是T中某个节点 */
/* 操作结果:若cur_e有右(下一个)兄弟,则返回它的右兄弟,否则返回"空"*/
int i;
for(i=0;i<T->n;i++)
if(T->nodes[i].data==cur_e)
/* 找到cur_e,其序号为i */
break;
if(T->nodes[i+1].parent==T->nodes[i].parent)
/* 根据树的构造函数,若cur_e有右兄弟的话则右兄弟紧接其后 */
return T->nodes[i+1].data;
return Nil;
}输出树
void Print(PTree *T){
/* 输出树T。加 */
int i;
printf("节点个数=%d\n",T->n);
printf(" 节点 父节点\n");
for(i=0;in;i++)
{
printf(" %c",Value(T,i)); /* 节点 */
if(T->nodes[i].parent>=0) /* 有父节点 */
printf(" %c",Value(T,T->nodes[i].parent)); /* 父节点 */
printf("\n");
}}向树中插入另一棵树
Status InsertChild(PTree *T,TElemType p,int i,PTree c){
/* 初始条件:树T存在,p是T中某个节点,1≤i≤p所指节点的度+1,非空树c与T不相交 */
/* 操作结果:插入c为T中p节点的第i棵子树 */
int j,k,l,f=1,n=0; /* 设交换标志f的初值为1,p的孩子数n的初值为0 */
PTNode t;
if(!TreeEmpty(T)) /* T不空 */ {
for(j=0;jn;j++) /* 在T中找p的序号 */
if(T->nodes[j].data==p) /* p的序号为j */
break;
l=j+1; /* 如果c是p的第1棵子树,则插在j+1处 */
if(i>1) /* c不是p的第1棵子树 */ {
for(k=j+1;kn;k++) /* 从j+1开始找p的前i-1个孩子 */
if(T->nodes[k].parent==j) /* 当前节点是p的孩子 */
{ n++; /* 孩子数加1 */
if(n==i-1) /* 找到p的第i-1个孩子,其序号为k1 */
break;
}
l=k+1; /* c插在k+1处 */
}
/* p的序号为j,c插在l处 */
if(ln)
/* 插入点l不在最后 */
for(k=T->n-1;k>=l;k--) /* 依次将序号l以后的节点向后移c.n个位置 */ {
T->nodes[k+c.n]=T->nodes[k];
if(T->nodes[k].parent>=l)
T->nodes[k+c.n].parent+=c.n;
}
for(k=0;knodes[l+k].data=c.nodes[k].data; /* 依次将树c的所有节点插于此处 */
T->nodes[l+k].parent=c.nodes[k].parent+l; }
T->nodes[l].parent=j; /* 树c的根节点的父节点为p */
T->n+=c.n; /* 树T的节点数加c.n个 */
while(f)
{ /* 从插入点之后,将节点仍按层序排列 */
f=0; /* 交换标志置0 */
for(j=l;jn-1;j++)
if(T->nodes[j].parent>T->nodes[j+1].parent) {/* 如果节点j的父节点排在节点j+1的父节点之后(树没有按层序排列),交换两节点*/
t=T->nodes[j];
T->nodes[j]=T->nodes[j+1];
T->nodes[j+1]=t;
f=1; /* 交换标志置1 */
for(k=j;kn;k++) /* 改变父节点序号 */
if(T->nodes[k].parent==j)
T->nodes[k].parent++; /* 父节点序号改为j+1 */
else
if(T->nodes[k].parent==j+1)
T->nodes[k].parent--; /* 父节点序号改为j */
}
}
return OK;
}
else /* 树T不存在 */
return ERROR;
} 删除子树
Status deleted[MAX_TREE_SIZE+1];
/* 删除标志数组(全局量) */
void DeleteChild(PTree *T,TElemType p,int i){
/* 初始条件:树T存在,p是T中某个节点,1≤i≤p所指节点的度 */ /* 操作结果:删除T中节点p的第i棵子树 */
int j,k,n=0;
LinkQueue q;
for(j=0;j<=T->n;j++)
/* 置初值为0(不删除标记) */
pq.name='a';
InitQueue(&q);
/* 初始化队列 */
for(j=0;j<T->n;j++)
break;
/* j为节点p的序号 */
for(k=j+1;k<T->n;k++) {
if(T->nodes[k].parent==j)
n++;
if(n==i)
break; /* k为p的第i棵子树节点的序号 */
}
if(k<T->n) /* p的第i棵子树节点存在 */ {
n=0;
pq.num=k;
deleted[k]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
while(!QueueEmpty(q)) {
DeQueue(&q,&qq);
for(j=qq.num+1;j<T->n;j++)
if(T->nodes[j].parent==qq.num)
{
pq.num=j;
deleted[j]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
}
}
for(j=0;j<T->n;j++)
if(deleted[j]==1)
{
for(k=j+1;k<=T->n;k++)
{
deleted[k-1]=deleted[k];
T->nodes[k-1]=T->nodes[k];
if(T->nodes[k].parent>j)
T->nodes[k-1].parent--;
}
j--;
}
T->n-=n;
/* n为待删除节点数 */
}
}层序遍历树
void TraverseTree(PTree *T,void(*Visit)(TElemType)){
/* 初始条件:二叉树T存在,Visit是对节点操作的应用函数 */ /* 操作结果:层序遍历树T,对每个节点调用函数Visit一次且仅一次 */
int i;
for(i=0;in;i++)
Visit(T->nodes[i].data);
printf("\n");}孩子链表表示法
存储结构[5]
/*树的孩子链表存储表示*/
typedef struct CTNode {
// 孩子节点
int child;
struct CTNode *next;
} *ChildPtr;
typede3.2 二叉树及存储结构
(1)顺序存储方式
typenode=record
data:datatype
l,r:integer;
end;
vartr:array[1..n]ofnode;
(2)链表存储方式,如:
typebtree=^node;
node=record
data:datatye;
lchild,rchild:btree;
end;3.3 二叉树的遍历
先序遍历
首先访问根,再先序遍历左(右)子树,最后先序遍历右(左)子树,C语言代码如下:
void XXBL(tree*root){
//DoSomethingwithroot
if(root->lchild!=NULL)
XXBL(root->lchild);
if(root->rchild!=NULL)
XXBL(root->rchild);
}
中序遍历
首先中序遍历左(右)子树,再访问根,最后中序遍历右(左)子树,C语言代码如下
void ZXBL(tree*root)
{
if(root->lchild!=NULL)
ZXBL(root->lchild);//DoSomethingwithroot
if(root->rchild!=NULL)
ZXBL(root->rchild);
}
后序遍历
首先后序遍历左(右)子树,再后序遍历右(左)子树,最后访问根,C语言代码如下
void HXBL(tree*root){
if(root->lchild!=NULL)
HXBL(root->lchild);
if(root->rchild!=NULL)
HXBL(root->rchild);//DoSomethingwithroot
}
层次遍历
即按照层次访问,通常用队列来做。访问根,访问子女,再访问子女的子女(越往后的层次越低)(两个子女的级别相同)例子:
范例二叉树:
A
B C
D E
此树的顺序结构为:ABCD##E
intmain()
{
node*p=newnode;
node*p=head;
head=p;
stringstr;
cin>>str;
creat(p,str,0)//默认根节点在str下标0的位置
return0;
}
//p为树的根节点(已开辟动态内存),str为二叉树的顺序存储数组ABCD##E或其他顺序存储数组,r当前结点所在顺序存储数组位置
void creat(node*p,stringstr,intr)
{
p->data=str[r];
if(str[r*2+1]=='#'||r*2+1>str.size()-1)p->lch=NULL;
else
{
p->lch=newnode;
creat(p->lch,str,r*2+1);
}
if(str[r*2+2]=='#'||r*2+2>str.size()-1)p->rch=NULL;
else
{
p->rch=newnode;
creat(p->rch,str,r*2+2);
}
}http://www.jianshu.com/p/45dd59940323
4.1 二叉搜索树
Size Balanced Tree(SBT)
AVL树
红黑树
Treap(Tree+Heap)
这些均可以使查找树的高度为O(log(n))
4.2 平衡二叉树
5.1 堆
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4…n/2)
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。[1]
支持的基本操作
堆支持以下的基本:
build:建立一个空堆;
insert:向堆中插入一个新元素;
update:将新元素提升使其符合堆的性质;
get:获取当前堆顶元素的值;
delete:删除堆顶元素;
heapify:使删除堆顶元素的堆再次成为堆。
5.2 哈夫曼树与哈夫曼编码
二叉树中有一种特别的树——哈夫曼树(最优二叉树),其通过某种规则(权值)来构造出一哈夫曼二叉树,在这个二叉树中,只有叶子节点才是有效的数据节点(很重要),其他的非叶子节点是为了构造出哈夫曼而引入的!
哈夫曼编码是一个通过哈夫曼树进行的一种编码,一般情况下,以字符:‘0’与‘1’表示。编码的实现过程很简单,只要实现哈夫曼树,通过遍历哈夫曼树,规定向左子树遍历一个节点编码为“0”,向右遍历一个节点编码为“1”,结束条件就是遍历到叶子节点!因为上面说过:哈夫曼树叶子节点才是有效数据节点!
首先就定义一个二叉树结构:
struct tree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;其中权值是我们最需要关心的,因为我们就是要通过权值来构造,但权值怎么规定呢?当然是根据实际情况来!其中叶子节点是为了标记是叶子节点,便于后期编码!
为了简单说明,第一个例子就直接定义多个哈夫曼树节点,然后通过这些节点来构造出最终的哈夫曼树!
tree tr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};tr是一个哈夫曼数组,其中每个元素都是一个哈夫曼树,我们的任务就是将这些元素“整合”起来,使它们联系起来构成一个哈夫曼树。初始时,数组每个元素都是没有联系的,我们的任务就是把它们通过struct tree *zuo,*you;//左右孩子 来连接起来,形象上就是构成一棵二叉树。
我们先通过语言叙述的方法来构造一棵哈夫曼二叉树:
a 权值5
b权值2
c权值9
d权值3
e权值6
首先,取权值最小的两个节点“整合”出一个新的节点,该节点的权值为最小两个节点权值之和。如下图:
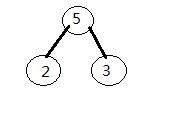
哈夫曼树详解、实现代码及哈夫曼编码实例
然后,将这个新的节点与剩下元素进行权值比较,依旧取最小的两个权值节点构造 新的节点,反复这个过程,直到取完所有元素,本例的哈夫曼树如下图:
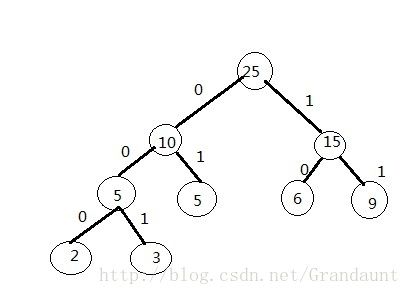
哈夫曼树详解、实现代码及哈夫曼编码实例
其中叶子节点(也就是2,3,5,6,9)是有效的数据节点!构造时节点的左右顺序并不影响哈
曼树的构造,但会导致出现不同的编码,当然编码只要不出现前缀码就是正确的编码。
实现算法:
实现算法有很多种,关键是要理解它构造的原理。
通过上面的例子,我们知道构造一个哈夫曼树,需要的节点数数有效数据节点的2*n-1,其中
n是有效数据的个数,如上面例子,有效数据个数有5个,但最终构造出的哈夫曼树有2*5-1=9
个节点,所以根据这个性质就可写出一种算法:
tree tr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};5个数据所以需要9个空间,其中9-5=4个空间是给那些无效节点使用的(哈夫曼树种非叶子节点)。
首先,我们遍历这个数组,找到最小的两个元素。
然后,将他们移动到前面,并将权值求和构造出新的节点,新的节点左右子树指向最小的两个元素,将这个新节点插入有效数据后面。
最后,从第2+1个元素(前面两个无需遍历了)开始重新遍历。
重复上述过程,直到数组填满,填满后的最后一个元素就是最终的哈夫曼树。
如第一次遍历后数组tr[9]状态就变为:
tree tr[9]={ {'d',true,3},{'b',true,2},{'c',true,9}, {'a',true,5},{'e',true,6},{‘’,false,5,tr[0],tr[1]}}最小的两个元素移到了前面,有效数据增加了一个,并且新节点左右子树指向前面两个元素。
完整哈夫曼实现代码如下;
// hfm.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
static int hfmb=0;
struct tree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;
struct shfm
{
char date;//字符数据
char bianm[11];//哈夫曼编码,最大编码数为11(可根据实际修改!)
}hfm[100];//哈夫曼编码对应真实数据表
void gettree(tree tr[],int shij,int youx)//构造哈夫曼树,tr树集合,shij集合实际数据个数,youx集合有效数据个数
{
//模拟动态增长数组,每次构造新的树就插入有效数据后面
if (2*youx-1!=shij)
{
printf("参数不符合!");
return;
}
int c=0;
while(youx!=shij)//当有效个数==实际个数时,构造完成!
{
for (int i=c;i
{
//每次循环取两个最小值并将两个最小值放置在当前循环起始两位
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c];
tr[c]=p;
}
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c+1];
tr[c+1]=p;
}
}
//以下为通过最小值构造的新树
tr[youx].quanzhi=tr[c].quanzhi+tr[c+1].quanzhi;
tr[youx].you=&tr[c];//新树右孩子指向当前循环的最小值之一
tr[youx].zuo=&tr[c+1];//新树左孩子指向当前循环的最小值之一
youx++;//新树插入当前有效数据个数后面 并使有效数据个数+1
c=c+2;
}
}
void bianltree(tree *tr,char ch[])//哈夫曼编码
{
//通过遍历树,得到每个节点的编码
static int i=0;
if (!tr->min)//叶子节点
{
ch[i]='0';
i++;
bianltree(tr->zuo,ch);//左节点编码为"0"
ch[i]='1';
i++;
bianltree(tr->you,ch);//右节点编码为"1"
}
if (tr->min)
{
ch[i]='\0';//结束标记()
printf("%c %s \n",tr->date,ch);
hfm[hfmb].date=tr->date;
int j=0;
while(j!=i||i>10)
{
hfm[hfmb].bianm[j]=ch[j];
j++;
}//保存编码映射表
hfmb++;
}
i--;//递归走入右叶子节点时,取消当前赋值(当前必为左边叶子节点)
}
int _tmain(int argc, _TCHAR* argv[])
{
tree tr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};
// printf("%d \n",sizeof(tr)/sizeof(tree));
gettree(tr,9,5);
char ch[100];
//printf("%s\n",ch);
bianltree(&tr[8],ch);
return 0;
}
哈夫曼树详解、实现代码及哈夫曼编码实例
其中gettree()函数是构造哈夫曼过程,bianltree()是通过哈夫曼树编码过程,struct shfm
结构体是保存字符数据与它的哈夫曼编码的映射表,可用也可不用,这里之所以使用,是因为通过一次遍历就可得到所有元素的编码,以后要编码只需查表即可,以空间换时间。
下面介绍哈夫曼的应用举例:
通过上文的介绍,下面就介绍哈夫曼的实际运用。
本例的模拟效果是:通过传入一串字符串,返回该字符串的编码。并且通过传入一个有效的编码得到一个字符串!
下面给出完整代码,该代码基于上述代码之上进行修改,并优化上述代码。
// hfm.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
static int hfmb=0;
struct tree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;
struct shfm
{
char date;//字符数据
int len;//编码长度
char bianm[11];//哈夫曼编码,最大编码数为11(可根据实际修改!)
}hfm[100];//哈夫曼编码对应真实数据表
void gettree(tree tr[],int shij,int youx)//构造哈夫曼树,tr树集合,shij集合实际数据个数,youx集合有效数据个数
{
//模拟动态增长数组,每次构造新的树就插入有效数据后面
if (2*youx-1!=shij)
{
printf("参数不符合!");
return;
}
int c=0;
while(youx!=shij)//当有效个数==实际个数时,构造完成!
{
for (int i=c;i
{
//每次循环取两个最小值并将两个最小值放置在当前循环起始两位
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c];
tr[c]=p;
}
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c+1];
tr[c+1]=p;
}
}
//以下为通过最小值构造的新树
tr[youx].quanzhi=tr[c].quanzhi+tr[c+1].quanzhi;
tr[youx].you=&tr[c];//新树右孩子指向当前循环的最小值之一
tr[youx].zuo=&tr[c+1];//新树左孩子指向当前循环的最小值之一
youx++;//新树插入当前有效数据个数后面 并使有效数据个数+1
c=c+2;
}
return ;
}
void bianltree(tree *tr)//哈夫曼编码
{
//通过遍历树,得到每个节点的编码
static char ch[100];
static int i=0;
if (!tr->min)//叶子节点
{
ch[i]='0';
i++;
bianltree(tr->zuo);//左节点编码为"0"
ch[i]='1';
i++;
bianltree(tr->you);//右节点编码为"1"
}
if (tr->min)
{
ch[i]='\0';//结束标记()
printf("%c %s \n",tr->date,ch);
hfm[hfmb].date=tr->date;
hfm[hfmb].len=i;
int j=0;
while(j!=i||i>10)
{
hfm[hfmb].bianm[j]=ch[j];
j++;
}//保存编码映射表
hfmb++;
}
i--;//递归走入右节点时,取消当前赋值(当前必为左边叶子节点)
}
void chushihuahmf(tree *hfmtree,char *str,int i)
{//初始化哈夫曼树数组!参数:含哈夫曼树数组,待编码数据串,数据串长度
int j=0;
while(*str)
{//初始化有效的数组元素
hfmtree->date=*str;//待编码数据
hfmtree->min=true;//是否叶子节点
hfmtree->quanzhi=*str;//权值
str++;
hfmtree++;
j++;
}
while(j<=2*i-2)
{
//初始化非有效数组元素
hfmtree->min=false;//全部非叶子节点
j++;
hfmtree++;
}
//注:本函数权值是根据字符ascll码判断!可根据实际情况重新定义初始化函数!
}
char * hfmbm(char *str)
{//哈夫曼编码函数 参数:待编码字符串!
int i=0;//统计字符串字符数
int j=i;
char *p=str;//备份字符串首地址
while(*str)//统计字符数
{
i++;
str++;
}
//printf("%d",i);
tree *hfmtree=(tree *)malloc(sizeof(tree)*(2*i-1));//根据字符数开辟可用空间
str=p;
tree *pp=hfmtree;//备份哈夫曼数组首地址
chushihuahmf(hfmtree,str,i);//根据ascll码制定权值并依此构造数组(根据实际情况可自行修改)
hfmtree=pp;
gettree(hfmtree,2*i-1,i);//构造一个哈夫曼树
tre=&hfmtree[2*i-2];//得到哈夫曼树
bianltree(tre);//通过哈夫曼树编码 并保存在编码
char *restr=(char *)malloc(sizeof(char)*i*11);//开辟编码后的字符串地址
int k=0;
p=restr;
while(k
{//通过遍历 编码映射表 编码字符 通过映射表的字符匹配后返回编码
int b=0;
while(b
{
if (hfm[b].date==str[k])
{
for (int j=0;j
{
*restr=hfm[b].bianm[j];
restr++;
}
break;
}
b++;
}
k++;
}
*restr='\0';
restr=p;
printf("编码完成:\n%s\n",restr);
return restr;
}
void hfmjm(char *hmf)
{//哈夫曼解码 参数哈夫曼编码后的数据串
tree *p=tre;//得到哈夫曼树
while(*hmf)
{
if (*hmf=='0')//编码为0走左子树
{
tre=tre->zuo;
if (tre->min)//为叶子节点
{
printf("%c",tre->date);//输出编码
tre=p;
}
hmf++;
continue;
}
if (*hmf=='1')//编码为1走右子树
{
tre=tre->you;
if (tre->min)
{
printf("%c",tre->date);
tre=p;
}
hmf++;
continue;
}
printf("不能识别编码:%c\n",*hmf);
return;
}
printf("\n");
tre=p;//还原哈夫曼树
//注:本解码是根据哈夫曼树解码 本程序还可以根据编码映射表解码
}
int _tmain(int argc, _TCHAR* argv[])
{
char *ch="abcd@#$3456asd";
printf("待编码数据位:%s\n",ch);
printf("编码格式:\n");
char *str=hfmbm(ch);
printf("解码:\n");
hfmjm(str);
//////解码测试:只要输入编码映射表(struct shmf结构体)有的编码 就能实现解码!
printf("\n解码测试:请根据已有编码格式输入编码\n");
char hmf[100];
gets(hmf);
printf("解码:\n");
hfmjm(hmf);
return 0;
}
函数说明:
char * hfmbm(char *str)函数是完成哈夫曼树构造的函数,用户只需传入一个带编码的字符串就可,本函数就可根据字符串开辟数组空间,并构造哈夫曼树。
void chushihuahmf(tree *hfmtree,char *str,int i)函数是初始化哈夫曼树权值的函数,因为我们构造时需要指定构造规则(即权值),本函数为了方便,直接使用ascll码作为权值构造,本函数可根据实际情况修改。
void hfmjm(char *hmf)函数是解码函数,通过传入有效编码解码出字符串!
我们发现相同元素有不同的编码,不过这不影响编码与解码,但从空间、时间角度应该避免这种情况,篇幅有效,本文将不再处理,在本例中由于有映射表,所有可以通过遍历映射表删除重复元素。
5.3 集合及运算
小白专场:堆中的路径 - C语言实现
6.1 什么是图
6.2 图的遍历
6.3 应用实例:拯救007
6.4 应用实例:六度空间
小白专场:如何建立图- C语言实现
树之习题选讲-Tree Traversals Again
树之习题选讲-Complete Binary Search Tree
树之习题选讲- Huffman Codes
7.1 最短路径问题
小白专场:哈利·波特的考试- C语言实现
第八讲 图(下)[陈越]
8.1 最小生成树问题
8.2 拓扑排序
图之习题选讲-旅游规划
第九讲 排序(上)[陈越]
9.1 简单排序(冒泡、插入)
9.2 希尔排序
9.3 堆排序
9.4 归并排序
第十讲 排序(下)[陈越]
10.1 快速排序
10.2 表排序
10.3 基数排序
10.4 排序算法的比较
11.1 散列表\哈希表
11.2 散列函数的构造方法
11.3 冲突处理方法
11.4 散列表的性能分析
11.5 应用实例:词频统计