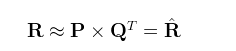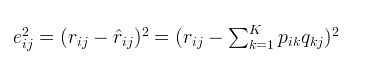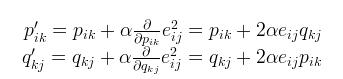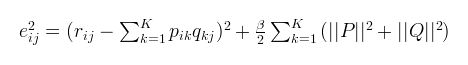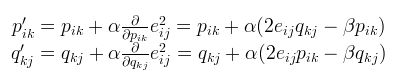推荐系统笔记(矩阵分解)

                         基于矩阵分解的推荐算法，简单入门

一，基于矩阵分解的推荐算法相关理论介绍

基本思想 

       正如其名称所暗示的那样，矩阵分解显然是对矩阵进行分解，即找出两个（或更多）矩阵，这样当你将它们相乘时，你将得到原始矩阵。

        推荐系统中的经典问题：评分预测(实际应用中，评分数据很难搜集到，属于典型的精英问题)，与之相对的问题是行为预测。鉴于每个用户已对系统中的某些项目进行评级，我们希望通过这些已知的数据预测用户尚未评级的项目，以便我们可以向用户提出建议。怎么预测这些评分呢，协同过滤(Collaborative Filtering)算法是最经典的方法。而协同过滤算法进一步划分又可分为三种。第一种是基于用户(user-based)的协同过滤，第二种是基于项目(item-based)的协同过滤，第三种是基于模型(model based)的协同过滤。

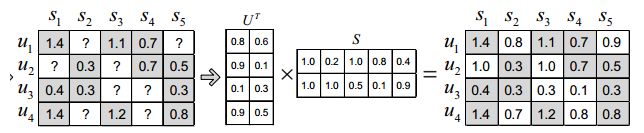
      基本矩阵分解（basic MF）:

        将评分矩阵R分解为用户矩阵U和项目矩阵S， 通过不断的迭代训练使得U和S的乘积越来越接近真实矩阵，矩阵分解过程如图： 

              

数学理论基础 

        矩阵分解算法的数学理论基础是矩阵的行列变换。在《线性代数》中，我们知道矩阵A进行行变换相当于A左乘一个矩阵，矩阵A进行列变换等价于矩阵A右乘一个矩阵，因此矩阵A可以表示为A=PEQ=PQ（E是标准阵）。

接下来我们对这个矩阵分解过程做具体分析：

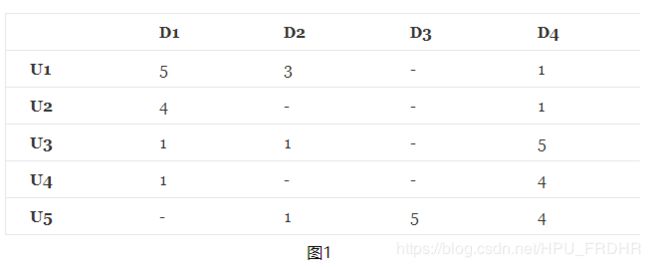
        现在假设现在我们有5个用户和10个项目，并且评级是从1到5的整数，矩阵可能看起来像下图1所示

       矩阵中，描述了5个用户(U1,U2,U3,U4 ,U5)对4个物品(D1,D2,D3,D4)的评分(1-5分)，- 表示没有评分，现在目的是把没有评分的 给预测出来，然后按预测的分数高低，给用户进行推荐。

       如何预测缺失的评分呢？对于缺失的评分，可以转化为基于机器学习的回归问题，也就是连续值的预测，对于矩阵分解有如下式子，R是类似图1的评分矩阵，假设N*M维(N表示行数，M表示列数)，可以分解为P跟Q矩阵，其中P矩阵维度N*K，P矩阵维度K*M。

                                                                     

         对于P,Q矩阵的解释，直观上，P矩阵是N个用户对K个主题的关系，Q矩阵是K个主题跟M个物品的关系，至于K个主题具体是什么，在算法里面K是一个参数，需要调节的，通常10~100之间。 

                                                                     

       对于式子2的左边项，表示的是R^ 第i行，第j列的元素值。对于如何衡量，我们分解的好坏呢？式子3，给出了衡量标准，也就是损失函数，平方项损失，最后的目标，就是每一个元素(非缺失值)的e(i,j)的总和 最小

                                                         

         OK，目前现在评分矩阵有了，损失函数也有了，该优化算法登场了，通常的优化方法分为两种：交叉最小二乘法（alternative least squares）和梯度下降法（stochastic gradient descent）。本文用梯度下降法作为优化方案。

 

梯度下降法

基于梯度下降的优化算法，p,q里面的每个元素的更新方式

                                                           

                                                        

       这里是一个常数，其值决定接近最小值的速率。通常我们会选择一个较小的值，比如0.0002。这是因为如果我们向最小值迈出太大的一步，我们可能会遇到错过最小值并最终在最小值附近振荡的风险。

 

正则

上述算法是用于分解矩阵的非常基本的算法。正则化矩阵分解（Regularized MF）是Basic MF的优化，该算法是引入正则化以避免过度拟合。其不是直接最小化损失函数，而是在损失函数基础上增加规范化因子，将整体作为损失函数。 即通过添加参数并修改平方误差来完成的，如下所示：

                                               

       相应的p,q矩阵各个元素的更新也换成了如下方式

                                                    

        至此，P,Q矩阵元素求出来了之后，就可以对R矩阵中未评分的位置预测出相应的分数。

将上述例子在Python中实现

import numpy


'''
     R：要分解的矩阵，维数N×M
     P：尺寸为N×K的初始矩阵
     Q：尺寸为M * K的初始矩阵
     K：潜在特征的数量
     steps：执行优化的最大步骤数
     alpha：学习率
     beta：正则化参数
'''
def matrix_factorization(R, P, Q, K, steps=5000, alpha=0.0002, beta=0.02):
    Q = Q.T
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j] > 0:
                    eij = R[i][j] - numpy.dot(P[i,:],Q[:,j])
                    for k in range(K):
                        P[i][k] = P[i][k] + alpha * (2 * eij * Q[k][j] - beta * P[i][k])
                        Q[k][j] = Q[k][j] + alpha * (2 * eij * P[i][k] - beta * Q[k][j])
        eR = numpy.dot(P,Q) #eR是通过构造的P,Q求出的替代R的矩阵
        e = 0    #e评估误差大小
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j] > 0:
                    e = e + pow(R[i][j] - numpy.dot(P[i,:],Q[:,j]), 2)
                    for k in range(K):
                        e = e + (beta/2) * ( pow(P[i][k],2) + pow(Q[k][j],2) )
        if e < 0.0001:
            break
    return P, Q.T , e


#构造数据
R = [
         [5,3,0,1],
         [4,0,0,1],
         [1,1,0,5],
         [1,0,0,4],
         [0,1,5,4],
    ]
R = numpy.array(R)

N = len(R)  #返回R矩阵行数
M = len(R[0])   #返回R矩阵列数
K = 2    #自定义参数K

P = numpy.random.rand(N,K) #随机生成N*K的P矩阵
Q = numpy.random.rand(M,K)  #随机生成M*k的Q矩阵
nP, nQ ,e= matrix_factorization(R, P, Q, K)

展示输出：

#分解R矩阵得到的两个矩阵
display(nP)
display(nQ)

 array([[5, 3, 0, 1],
       [4, 0, 0, 1],
       [1, 1, 0, 5],
       [1, 0, 0, 4],
       [0, 1, 5, 4]])

array([[4.9847435 , 2.96237303, 3.57028979, 0.99886405],
       [3.97318163, 2.37243338, 3.05171992, 0.99710432],
       [1.04700635, 0.88752572, 5.6200773 , 4.96141988],
       [0.97701747, 0.79144657, 4.56975433, 3.97154804],
       [1.55987267, 1.13476366, 4.93092436, 4.03341721]])

#原矩阵R
display(R)
#通过构造的P,Q求出的替代R的矩阵
display(numpy.dot(nP,nQ.T))
#误差大小
e

 array([[5, 3, 0, 1],
       [4, 0, 0, 1],
       [1, 1, 0, 5],
       [1, 0, 0, 4],
       [0, 1, 5, 4]])

array([[4.9847435 , 2.96237303, 3.57028979, 0.99886405],
       [3.97318163, 2.37243338, 3.05171992, 0.99710432],
       [1.04700635, 0.88752572, 5.6200773 , 4.96141988],
       [0.97701747, 0.79144657, 4.56975433, 3.97154804],
       [1.55987267, 1.13476366, 4.93092436, 4.03341721]])

1.1489407697144327

         我们可以看到，对于现有的评级，我们的近似值非常接近真实值，我们也得到了一些未知值的“预测”。上述代码将特征的数量（Python代码中的K）设为2时，算法能够将用户和项目关联到两个不同的特征，并且预测也遵循这些关联。例如，我们可以看到D4上的U4的预测等级是4.59，因为U4和U5都将D4评为高。

 

矩阵分解有如下优点：

1. 可解释性很差，其隐空间中的维度无法与现实中的概念对应起来；

2. 训练速度慢，不过可以通过离线训练来弥补这个缺点；

3. 实际推荐场景中往往只关心topn结果的准确性，此时考察全局的均方差显然是不准确的。

相对的，矩阵分解的缺点则有：

1. 可解释性很差，其隐空间中的维度无法与现实中的概念对应起来；

2. 训练速度慢，不过可以通过离线训练来弥补这个缺点；

3. 实际推荐场景中往往只关心topn结果的准确性，此时考察全局的均方差显然是不准确的。

参考资料

1.https://www.cnblogs.com/kobedeshow/p/3651833.html

2.http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/#source-code