山东大学机器学习(实验一解读)——线性回归
网上关于线性回归的介绍已经很详细,结合课堂老师所讲的内容,下面是我个人的实验所做的内容,老师大部分实验都是斯坦福上的,不过要自己理解和学习需要自己实现其实也不难。我会以matlab代码形式展示给大家,希望对你们有帮助,有错误还望大家指正。
1. 2D线性回归
- 2D线性线性回归模型
h θ ( x ) = θ T x = ∑ i = 0 1 θ i x i = θ 0 + θ 1 x 1 h_\theta(x)=\theta^Tx=\sum_{i=0}^1\theta_ix_i=\theta_0+ \theta_1x_1 hθ(x)=θTx=i=0∑1θixi=θ0+θ1x1 - 梯度下降算法
注意你选择的是梯度下降算法还是随机梯度下降算法,这两者是有区别的,具体的可以自行百度,我使用的是梯度下降算法。
- 实验内容
(1)使用 α = 0.07 \alpha = 0.07 α=0.07的学习率实施梯度下降。初始化参数 θ = 0 ⃗ ( i . e . , θ 0 = θ 1 = 0 ) \theta = \vec{0}(i.e.,\theta_0 = \theta_1 = 0) θ=0(i.e.,θ0=θ1=0),并从该初始起点开始一次梯度下降迭代。 记录第一次迭代后得到的 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1的值。
x = load('ex1_1x.dat');
y = load('ex1_1y.dat');
m = length(y) ; % store the number of training examples
x = [ones(m,1),x] ; % Add a column of ones to x
alpha = 0.07; %learning rate
%initial theta
theta0 = 0;
theta1 = 0;
%after one iteration
theta0 = theta0 - alpha*(1/m)*sum((theta0.*x(:,1)+theta1.*x(:,2)- y).*x(:,1));
theta1 = theta1 - alpha*(1/m)*sum((theta0.*x(:,1)+theta1.*x(:,2)- y).*x(:,2));
结果: θ 0 = 0.0745 , θ 1 = 0.3543 \theta_0=0.0745,\theta_1=0.3543 θ0=0.0745,θ1=0.3543
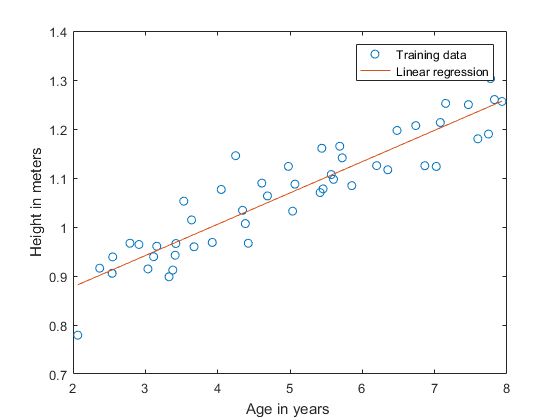
(2)继续运行梯度下降以进行更多迭代,直到 θ \theta θ收敛为止(这将总共需要大约1500次迭代)。收敛后,记录你得到的最终值 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1,根据 θ \theta θ,将你的算法中的直线绘制在与训练数据相同的图表上。
x = load('ex1_1x.dat');
y = load('ex1_1y.dat');
figure % open a new figure window
plot (x , y , ' o ' );
ylabel ( ' Height in meters ' );
xlabel ( 'Age in years ' );
m = length(y) ; % store the number of training examples
x = [ones(m,1),x] ; % Add a column of ones to x
alpha = 0.07; %learning rate
theta0(1,1) = 0;
theta1(1,1) = 0;
maxIter = 1500; %max iteration
tol = 1e-8;
for i = 1:maxIter
theta0(i+1,1) = theta0(i,1) - alpha*(1/m)*sum((theta0(i,1).*x(:,1)+theta1(i,1).*x(:,2)- y).*x(:,1));
theta1(i+1,1) = theta1(i,1) - alpha*(1/m)*sum((theta0(i,1).*x(:,1)+theta1(i,1).*x(:,2)- y).*x(:,2));
theta_before = [theta0(i,1);theta1(i,1)];
theta_now = [theta0(i+1,1);theta1(i+1,1)];
J_before = (0.5/m)*sum(x*theta_before - y);
J_now = (0.5/m)*sum(x*theta_now - y);
if abs(J_now - J_before) < tol
break;
end
end
hold on;
plot( x(:,2),theta0(i+1,1) + x(:,2)*theta1(i+1,1),'-');
legend( ' Training data ' , ' Linear regression ' );
结果: θ 0 = 0.7501 , θ 1 = 0.0639 \theta_0 = 0.7501, \theta_1 = 0.0639 θ0=0.7501,θ1=0.0639,迭代次数取决于你的阈值tol。
绘制图像如下:
(3)最后,我们想使用学到的假设做出一些预测。使用您的模型预测两个3.5岁和7岁男孩的身高。
3.5岁: θ 0 + 3.5 θ 1 = 0.7501 + 3.5 × 0.0639 = 0.9738 ≈ 1.0 \theta_0+3.5\theta_1=0.7501+3.5 \times 0.0639=0.9738 \approx 1.0 θ0+3.5θ1=0.7501+3.5×0.0639=0.9738≈1.0m
7岁: θ 0 + 7 θ 1 = 0.7500 + 3.5 × 0.0639 = 1.1973 ≈ 1.2 \theta_0+7\theta_1=0.7500+3.5 \times 0.0639=1.1973 \approx 1.2 θ0+7θ1=0.7500+3.5×0.0639=1.1973≈1.2m
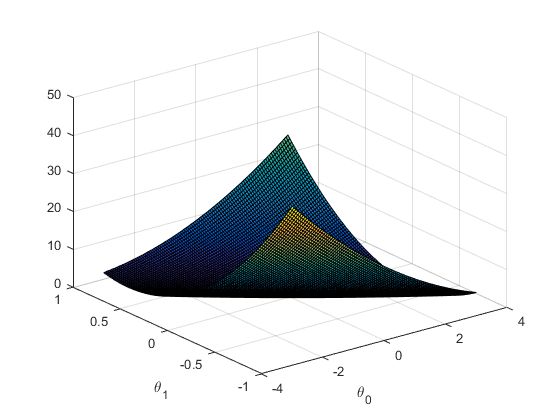
2. 理解 J ( θ ) J(\theta) J(θ)
J_vals = zeros (100 , 100) ; % initialize Jvals to
% 100*100 matrix of 0's
theta0_vals = linspace (-3 , 3 , 100) ;
theta1_vals = linspace (-1 , 1 , 100) ;
% 对于linespace(x1,x2,N),其中x1、x2、N分别为起始值、终止值、元素个数。
for i = 1 : length (theta0_vals)
for j = 1 : length (theta1_vals )
t = [theta0_vals(i); theta1_vals(j)] ;
J_vals(i,j) = (0.5/m)*(x*t-y)'*(x*t-y);
end
end
J_vals = J_vals'; %转置
figure ;
surf(theta0_vals,theta1_vals,J_vals);
xlabel ('\theta_0 ');ylabel('\theta_1');
绘制图片如下:
3. 多元线性回归
%-----------------函数func.m----------------------
function [theta,J] = func(alpha)
x = load('ex1_2x.dat');
y = load('ex1_2y.dat');
m = length(y);
x = [ones(m,1),x];
%数据标准化,减少迭代次数,加快梯度下降速度
sigma = std(x);
mu = mean(x);
x(:,2) = (x(:,2) - mu(2))./sigma(2);
x(:,3) = (x(:,3) - mu(3))./sigma(3);
theta = zeros(size(x(1,:)))'; %初始化theta
J = zeros(50,1); %初始代价矩阵
for i = 1:50
h = x * theta; %拟合函数
E = h - y;
J(i,1) = (0.5/m)*(E'*E);
theta = theta - (alpha/m)*x'*E;
end
end
%-----------------exp1_3.m----------------------
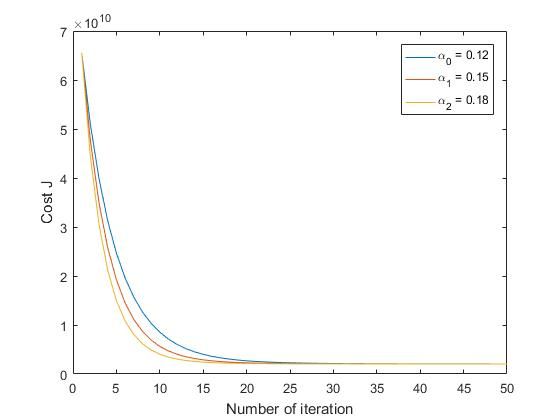
alpha = [0.12,0.15,0.18];
data = load('ex1_2x.dat');
store_theta = zeros(size(alpha,2),size(data,2)+1);
for i = 1:length(alpha)
[theta,J] = func(alpha(i));
store_theta(i,:) = theta;
plot(1:50,J);
hold on;
end
xlabel('Number of iteration');
ylabel('Cost J');
legend( '\alpha_0 = 0.12' , '\alpha_1 = 0.15' , '\alpha_2 = 0.18');
\quad\quad 注意,不同的学习率 α \alpha α所绘制的图片会有所不同,得到的最终 θ \theta θ也会有所不同。这个只是一个样例代码,你可以根据自身情况选择学习率,另外注意的是最终得到的 θ \theta θ拿来预测房价时是数据标准化后的房价,需要还原回去才会得到我们最终真实的房价。
\quad\quad 选择的学习率过小,收敛速度会比较慢。学习率过大,有可能导致代价函数错过最优解,从图像中我们会发现代价函数呈现出指数性增长,不断远离最优点。(你可以在代码中改动 α \alpha α值观察)