卡尔曼滤波 (Kalman Filter)
1.卡尔曼滤波的动机(Kalman Filter Motivation)
如何利用卡尔曼滤波来进行机器人学的贝叶斯估计?
卡尔曼滤波器是一种广泛使用的针对线性系统的最优跟踪算法,一些跟踪的例子包括自动驾驶汽车追踪行人和车辆,或者追踪装配线(assembly line)中在传送带(conveyor belt)上运动的部件。
我们将讨论卡尔曼滤波器(Kalman filter)的系统模型和测量模型,接着我们将讨论滤波器中的最大后验估计,最后,我们将把线性卡尔曼的思想扩展到非线性模型。
我们将学习时间序列建模,利用卡尔曼滤波器来估计世界的状态。在机器人统计学中的高斯分布 这篇文章中,我们的足球机器人已经学会了检测球的颜色,但是,在一场球赛中,球不会只停在一个地方,因此机器人需要跟踪球的轨迹,甚至预测球未来的运动,许多现实中的机器人都需要做相同的估计。在下图中,小球不断在地面上滚动,但是由于摩擦力的原因,小球越来越慢,除了预测小球的位置,机器人需要辨识出球在环境中的动力学特性。

另一个常见的影响现实世界物体的力——重力。在下图中,小球正在加速朝着地面下降,跟踪球的滤波器应该能建立模型描绘这种行为。

机器人应该对不确定性有些概念,如果机器人不确定球是怎么动的,它就不可能准确的做出相应的行为。当机器人被放到现实世界中的时候,它将从摄像头获得稳定的视频流,应用在机器人统计学中的高斯分布 的原理,机器人应该能够从传感器数据中确定球的位置,但是由于噪声的存在,这个位置可能并不十分准确,因此,机器人将有一堆带有噪声的数据。这些数据可以在任何时候近似地给出小球真实的状态,这一部分的内容重点就是计算这些状态。

我们应该分清测量结果的概念与真实状态的概念,真实世界有其投影,但是机器人只能观察到真实世界的一个投影。例如,球距离机器人的真实距离是11米,但是机器人认为距离是11.32567米。机器人通过摄像头观察到这个位置,而这个从摄像头获得的测量给出了对真实状态的带有噪声的估计。一个可能的噪声来源是代表小球的像素和代表周围区域被错误的识别了。机器人为了做出行动决策,关心的是隐藏状态的高层(high level)概念。
例如,足球机器人只关心球的位置、速度。对一些无人机,姿态就变成了一个特别重要的状态,它可以通过惯性测量单元或GPS进行测量。灭火机器人可能希望追踪火焰,这需要温度的信息来增加对颜色和大小的估计。每种任务都是不同的,所以搞清楚状态由什么构成非常重要。

在这部分我们只需要跟踪球的位置和速度,因此我们的状态由x、y、z坐标和dx、dy、dz组成,当我们测量状态时,我们并不总能获得与状态的形式相一致的信息,例如跟踪小球的时候,我们只对位置进行了观察,没有对速度的直接测量。这些测量与实际状态的差别使追踪变得困难。如下图所示,右图为机器人跟踪红色小球的位置曲线,可以发现数据包含了很多的噪声。

2.卡尔曼滤波模型(Kalman Filter Model)
动力系统和一般滤波器背后的测量模型。
2.1 线性模型(Linear Modeling)
动力系统的数学形式还有概率组成了模型的运动和噪声。为了启发大家,这里使用一个位置跟踪的例子,为了跟踪一个动目标,机器人必须建立其运动的动力系统的模型。动力系统描述了目标实时变化的状态以及机器人如何测量这些状态。
在这个简单的例子中,状态 x t x_{t} xt 表示 t t t 时刻的状态 x x x, 状态量包括以米为单位的位置 v v v 和 以米每秒为单位的速度 $dv/dt $。由于其动力学特点,状态随着每个时间点而改变。
从现在的时间点 t t t到下一点时间点 t + 1 t+1 t+1,这个变化由状态转移矩阵 A A A来表示,状态转移矩阵结合了状态信息,来描述下一个时间点的状态。这种转换简化了现在的状态,使其仅仅依赖之前的状态,这样使得数学问题更加简单。
通过位置和速度的状态,我们知道位置必须基于速度才能实时变化,状态转移矩阵通过给定的公式表现这种关系。
机器人不是直接测量 x x x,而是通过它的传感器观测 x x x的部分,这个部分称为 z z z, 这里状态和测量之间的关系由混合矩阵 C C C来表示, 即 z t = C x t z_{t}=Cx_{t} zt=Cxt。 为了完整性, u u u也考虑在内, u u u 代表不依赖于状态 x x x的外部输入, 我们在这一模块中不考虑 u u u,所以将其设为0, 即 x t + 1 = A x t + B u t x_{t+1}=Ax_{t}+Bu_{t} xt+1=Axt+But
在这个模型中X和Z均包含了噪声,状态X是有噪声的,因为线性模型没有捕捉到所有的物理学的相互作用。观察量Z有噪声,因为传感器在 测量时会收到噪声干扰。
2.2 卡尔曼滤波:贝叶斯滤波(KF:Bayesian filtering)
基于动力学模型,我们可以建立一个信息表。在任意给定的时间,我们知道俩部分信息,前一个状态 t − 1 t-1 t−1时刻的状态 x t − 1 x_{t-1} xt−1和现状态的测量量 t t t时刻的观测量 z t z_{t} zt。有了这俩个信息后,我们想计算出现在 t t t 时刻的状态 x t x_{t} xt。
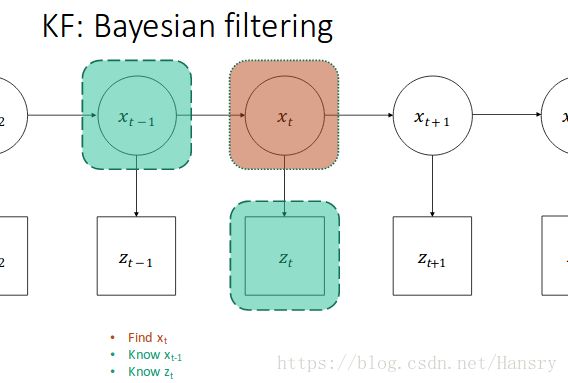
**1).**值得注意的是,我们不相信测量结果中的任意单一的量。为了获得包含这种不确定的估计,我们将这个动力学模型转换成一系列概率表达。给定了系统动力学量,基于前一状态概率条件之上的现在状态的概率,即 p ( x t ∣ x t − 1 ) p(x_{t}|x_{t-1}) p(xt∣xt−1),这意味这我们当前的状态不能离之前的状态太远。
还有一件值得注意的是,要把传感器得到的 Z Z Z 和真实状态 x x x 联系起来。我们的传感器仅仅给我们单一测量值,但是我们想要一个概率分布,为了完成这个任务,我们估计了基于t时刻状态条件下获得当前测量值的条件概率 p ( z t ∣ x t ) p(z_{t}|x_{t}) p(zt∣xt)。例如,我们正前方的一个球提供了一个方差很小的确切估计(certain estimation),然而,有一定距离的观察会有一个比较大的方差,因为我们不知道准确距离是多少。
我们将继续使用高斯分布作为数学模型,对于一般滤波器,这意味着选择一个猜测性的机制,建立含有均值和用n表示的方差这样状态的模型 p ( x t ) = N ( x t , P t ) p(x_{t})=N(x_{t}, P_{t}) p(xt)=N(xt,Pt)。
==========================================================================
Prediction using state dynamic model
p ( x t ∣ x t − 1 ) p(x_{t}|x_{t-1}) p(xt∣xt−1)
Inference from noisy measurements
p ( z t ∣ x t ) p(z_{t}|x_{t}) p(zt∣xt)
Model x t x_{t} xt with a Gaussian (mean and covariance)
p ( x t ) = N ( x t , P t ) p(x_{t})=N(x_{t},P_{t}) p(xt)=N(xt,Pt)
==========================================================================
**2).**现在我们有俩个动力系统模型和概率模型,我们可以结合俩个想法。
首先,线性动力系统模型表示我们可以用状态转移矩阵 A A A来建立基于现在状态的下个状态的条件概率, 即 p ( x t ∣ x t − 1 ) = A p ( x t − 1 ) p(x_{t}|x_{t-1})=Ap(x_{t-1}) p(xt∣xt−1)=Ap(xt−1)。 此外,t时刻的测量值z的概率可以用动力系统模型的矩阵 C C C来建立关系,即 p ( z t ∣ x t ) = C p ( x t ) p(z_{t}|x_{t})=Cp(x_{t}) p(zt∣xt)=Cp(xt)。
我们通过新的m和o将噪声添加到测量(measurements)和观测(observation)系统中。使用高斯概率分布模型,状态和噪声可以用均值和方差来表示,即 p ( x t ∣ x t − 1 ) = A N ( x t − 1 , P t − 1 ) + N ( 0 , Σ m ) p(x_{t}|x_{t-1})=AN(x_{t-1}, P_{t-1})+N(0,\Sigma_{m}) p(xt∣xt−1)=AN(xt−1,Pt−1)+N(0,Σm), p ( z t ∣ x t ) = C N ( x t , P t ) + N ( 0 , Σ o ) p(z_{t}|x_{t})= CN(x_{t}, P_{t})+N(0,\Sigma_{o}) p(zt∣xt)=CN(xt,Pt)+N(0,Σo)
==========================================================================
Apply linear dynamics
p ( x t ∣ x t − 1 ) = A p ( x t − 1 ) p(x_{t}|x_{t-1})= Ap(x_{t-1}) p(xt∣xt−1)=Ap(xt−1)
p ( z t ∣ x t ) = C p ( x t ) p(z_{t}|x_{t})= Cp(x_{t}) p(zt∣xt)=Cp(xt)
Add noise for motion and observations
p ( x t ∣ x t − 1 ) = A p ( x t − 1 ) + v m p(x_{t}|x_{t-1})= Ap(x_{t-1})+v_{m} p(xt∣xt−1)=Ap(xt−1)+vm
p ( z t ∣ x t ) = C p ( x t ) + v o p(z_{t}|x_{t})= Cp(x_{t})+v_{o} p(zt∣xt)=Cp(xt)+vo
Introduce Guassian model of x_{t-1} and x_{t}
p ( x t ∣ x t − 1 ) = A N ( x t − 1 , P t − 1 ) + N ( 0 , Σ m ) p(x_{t}|x_{t-1})= AN(x_{t-1},P_{t-1})+N(0,\Sigma_{m}) p(xt∣xt−1)=AN(xt−1,Pt−1)+N(0,Σm)
p ( z t ∣ x t ) = C N ( x t , P t ) + N ( 0 , Σ o ) p(z_{t}|x_{t})= CN(x_{t},P_{t})+N(0,\Sigma_{o}) p(zt∣xt)=CN(xt,Pt)+N(0,Σo)
==========================================================================
**3).**结合状态和测量之前,我们可以基于高斯分布的性质来合并上面的表达,首先,我们通过矩阵A和C进行线性变换,对高斯变化进行线性变换,得到均值和方差产生相应变化为另一个高斯分布,同样的,俩个高斯分布相加会得到另一个高斯分布。新的均值和方差是原先分布均值和方差的和 。
==========================================================================
Consolidate expression using special properties
p ( x t ∣ x t − 1 ) = A N ( x t − 1 , P t − 1 ) + N ( 0 , Σ m ) p(x_{t}|x_{t-1})=AN(x_{t-1},P_{t-1})+N(0,\Sigma_{m}) p(xt∣xt−1)=AN(xt−1,Pt−1)+N(0,Σm)
p ( z t ∣ x t ) = C N ( x t , P t ) + N ( 0 , Σ o ) p(z_{t}|x_{t})= CN(x_{t},P_{t})+N(0,\Sigma_{o}) p(zt∣xt)=CN(xt,Pt)+N(0,Σo)
Apply linear transform to Gaussian distributions
p ( x t ∣ x t − 1 ) = p ( A x t − 1 , A P t − 1 A T ) + N ( 0 , Σ m ) p(x_{t}|x_{t-1})= p(Ax_{t-1},AP_{t-1}A^{T})+N(0,\Sigma_{m}) p(xt∣xt−1)=p(Axt−1,APt−1AT)+N(0,Σm)
p ( z t ∣ x t ) = p ( C x t , C P t C T ) + N ( 0 , Σ o ) p(z_{t}|x_{t})= p(Cx_{t},CP_{t}C^{T})+N(0,\Sigma_{o}) p(zt∣xt)=p(Cxt,CPtCT)+N(0,Σo)
Apply summation
p ( x t ∣ x t − 1 ) = N ( A x t − 1 , A P t − 1 A T + Σ m ) p(x_{t}|x_{t-1})= N(Ax_{t-1},AP_{t-1}A^{T}+\Sigma_{m}) p(xt∣xt−1)=N(Axt−1,APt−1AT+Σm)
p ( z t ∣ x t ) = N ( C x t , C P t C T + Σ o ) p(z_{t}|x_{t})= N(Cx_{t},CP_{t}C^{T}+\Sigma_{o}) p(zt∣xt)=N(Cxt,CPtCT+Σo)
==========================================================================
但是这俩个概率分布如何融合起来提供真实状态更好的估计呢?
2.3 最大后验估计技术(Maximum-A-Posterior Estimation,MAP)
已经知道的信息:
1. 贝叶斯法则(Bayes‘ Rule)
p ( α ∣ β ) = P ( β ∣ α ) P ( α ) P ( β ) p(\alpha|\beta)=\frac{P(\beta|\alpha)P(\alpha)}{P(\beta)} p(α∣β)=P(β)P(β∣α)P(α)
2.已经知道的卡尔曼模型:
p ( x t ∣ x t − 1 ) = N ( A x t − 1 , A P t − 1 A T + Σ m ) p(x_{t}|x_{t-1})=N(Ax_{t-1}, AP_{t-1}A^{T}+\Sigma_{m}) p(xt∣xt−1)=N(Axt−1,APt−1AT+Σm)
p ( z t ∣ x t ) = N ( C x t , C P t C T + Σ o ) p(z_{t}|x_{t})=N(Cx_{t},CP_{t}C^{T}+\Sigma_{o}) p(zt∣xt)=N(Cxt,CPtCT+Σo)
在动力系统中,给定上一时刻状态下,当前时刻状态的概率可以用先验信息 α \alpha α表示,即 p ( α ) p(\alpha) p(α)。代表着测量模型信息的 β \beta β同时提供了观测证据,在给定的状态下,这个证据表示着一种被称作似然函数的约束概率 p ( α ∣ β ) p(\alpha|\beta) p(α∣β), 因此,
p ( x t ∣ x t − 1 ) = N ( A x t − 1 , A P t − 1 A T + Σ m ) — — > α ( P r i o r ) p(x_{t}|x_{t-1})=N(Ax_{t-1}, AP_{t-1}A^{T}+\Sigma_{m}) \ ——> \alpha \ (Prior) p(xt∣xt−1)=N(Axt−1,APt−1AT+Σm) ——>α (Prior)
p ( z t ∣ x t ) = N ( C x t , C P t C T + Σ o ) — — > β ∣ α ( L i k e l i h o o d ) p(z_{t}|x_{t})=N(Cx_{t},CP_{t}C^{T}+\Sigma_{o}) \ ——> \beta | \alpha \ (Likelihood) p(zt∣xt)=N(Cxt,CPtCT+Σo) ——>β∣α (Likelihood)
因此我们可以得到后验:
p ( x t ∣ z t , x t − 1 ) = p ( z t ∣ x t , x t − 1 ) p ( x t ∣ x t − 1 ) p ( z t ) \mathbf{p(x_{t}|z_{t},x_{t-1}) =\frac{p(z_{t}|x_{t},x_{t-1})p(x_{t}|x_{t-1})}{p(z_{t})}} p(xt∣zt,xt−1)=p(zt)p(zt∣xt,xt−1)p(xt∣xt−1) , 即为后验(Posterior)
后验概率表示我们对t时刻状态x的最优估计, 在给定先前 t − 1 t-1 t−1时刻的状态 x x x和观测 z t z_{t} zt的条件最优的估计。
最大后验估计可以给出这个分布的最优估计,该估计将会为求出 t时刻的状态 x t x_{t} xt 所服从的高斯分布的新的均值提供基础。
最大后验估计被写成对后验分布取值的最优化问题, 即
x t ^ = a r g m a x x t p ( x t ∣ z t , x t − 1 ) = a r g m a x x t p ( z t ∣ x t ) p ( x t ∣ x t − 1 ) p ( z t ) = a r g m a x x t p ( z t ∣ x t ) p ( x t ∣ x t − 1 ) \hat{x_{t}} = \underset{x_{t}}{argmax}\ p(x_{t}|z_{t},x_{t-1}) \\=\underset{x_{t}}{argmax} \ \frac{p(z_{t}|x_{t})p(x_{t}|x_{t-1})}{p(z_{t})} \\ =\underset{x_{t}}{argmax} \ p(z_{t}|x_{t})p(x_{t}|x_{t-1}) xt^=xtargmax p(xt∣zt,xt−1)=xtargmax p(zt)p(zt∣xt)p(xt∣xt−1)=xtargmax p(zt∣xt)p(xt∣xt−1) (这里x_{t} 与 z_{t} 无关)
则最后化为: x t ^ = a r g m a x x t N ( C x t , C P t C T + Σ o ) N ( A x t − 1 , A P t − 1 A T + Σ m ) . . . . . . . ( 1 ) \hat{x_{t}} = \underset{x_{t}}{argmax} \ N(Cx_{t}, CP_{t}C^{T}+\Sigma_{o})N(Ax_{t-1}, AP_{t-1}A^{T}+\Sigma_{m}) \ .......(1) xt^=xtargmax N(Cxt,CPtCT+Σo)N(Axt−1,APt−1AT+Σm) .......(1)
我们这里忽略与状态不独立部分的概率。最后我们得到一个最大化高斯分布乘积的问题,计算MAP估计的一个技巧是对这个乘积取对数,对数函数是单调递增函数,所以对数函数中 x t x_{t} xt的最优值,也是原函数中 x t x_{t} xt的最优值。
令 P = P t = A P t − 1 A T + Σ m ; R = C P t C T + Σ o P=P_{t}=AP_{t-1}A^{T}+\Sigma_{m}\ ; R= CP_{t}C^{T}+\Sigma_{o} P=Pt=APt−1AT+Σm ;R=CPtCT+Σo
引入高斯模型: p ( x ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ 1 / 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x)=\frac{1}{{(2\pi)}^{D/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)) p(x)=(2π)D/2∣Σ∣1/21exp(−21(x−μ)TΣ−1(x−μ))
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
对公式(1) 取对数,
x t ^ = a r g m a x x t l n 1 ( 2 π ) D / 2 ∣ R ∣ 1 / 2 e x p ( − 1 2 ( z t − C x t ) T R − 1 ( z t − C x t ) ) ∗ 1 ( 2 π ) D / 2 ∣ P ∣ 1 / 2 e x p ( − 1 2 ( x t − A x t − 1 ) T P − 1 ( x t − A x t − 1 ) ) = a r g m a x x t l n e x p ( − 1 2 ( z t − C x t ) T R − 1 ( z t − C x t ) ) ∗ e x p ( − 1 2 ( x t − A x t − 1 ) T P − 1 ( x t − A x t − 1 ) ) ( 这 里 将 常 数 去 掉 , 并 不 影 响 最 终 结 果 ) = a r g m a x x t ( − 1 2 ( z t − C x t ) T R − 1 ( z t − C x t ) ) + ( − 1 2 ( x t − A x t − 1 ) T P − 1 ( x t − A x t − 1 ) ) = a r g m i n x t ( ( z t − C x t ) T R − 1 ( z t − C x t ) + ( x t − A x t − 1 ) T P − 1 ( x t − A x t − 1 ) ) ( 转 化 为 最 小 化 问 题 ) . . . . . . . . ( 2 ) \hat{x_{t}} = \underset{x_{t}}{argmax} \ ln \ \frac{1}{(2\pi)^{D/2}|R|^{1/2}}exp(-\frac{1}{2}(z_{t}-Cx_{t})^{T}\ R^{-1} \ (z_{t}-Cx_{t}))* \ \frac{1}{(2\pi)^{D/2}|P|^{1/2}}exp(-\frac{1}{2}(x_{t}-Ax_{t-1})^{T}\ P^{-1} \ (x_{t}-Ax_{t-1})) \\ = \underset{x_{t}}{argmax} \ ln \ exp(-\frac{1}{2}(z_{t}-Cx_{t})^{T}\ R^{-1} \ (z_{t}-Cx_{t}))*exp(-\frac{1}{2}(x_{t}-Ax_{t-1})^{T}\ P^{-1} \ (x_{t}-Ax_{t-1})) (这里将常数去掉,并不影响最终结果)\\ =\underset{x_{t}}{argmax} \ (-\frac{1}{2}(z_{t}-Cx_{t})^{T}\ R^{-1} \ (z_{t}-Cx_{t}))\ + \ (-\frac{1}{2}(x_{t}-Ax_{t-1})^{T}\ P^{-1} \ (x_{t}-Ax_{t-1})) \\= \underset{x_{t}}{argmin} \ ((z_{t}-Cx_{t})^{T}\ R^{-1} \ (z_{t}-Cx_{t})\ + \ (x_{t}-Ax_{t-1})^{T}\ P^{-1} \ (x_{t}-Ax_{t-1})) (转化为最小化问题) \ ........(2) xt^=xtargmax ln (2π)D/2∣R∣1/21exp(−21(zt−Cxt)T R−1 (zt−Cxt))∗ (2π)D/2∣P∣1/21exp(−21(xt−Axt−1)T P−1 (xt−Axt−1))=xtargmax ln exp(−21(zt−Cxt)T R−1 (zt−Cxt))∗exp(−21(xt−Axt−1)T P−1 (xt−Axt−1))(这里将常数去掉,并不影响最终结果)=xtargmax (−21(zt−Cxt)T R−1 (zt−Cxt)) + (−21(xt−Axt−1)T P−1 (xt−Axt−1))=xtargmin ((zt−Cxt)T R−1 (zt−Cxt) + (xt−Axt−1)T P−1 (xt−Axt−1))(转化为最小化问题) ........(2)
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
在新的表达式中,即公式(2),我们对它求导并使导数为0来求解它, 即
0 = d ( z t − C x t ) T R − 1 ( z t − C x t ) + ( x t − A x t − 1 ) T P − 1 ( x t − A x t − 1 ) d x t . . . . . . ( 3 ) 0=\frac{d(z_{t}-Cx_{t})^{T}\ R^{-1} \ (z_{t}-Cx_{t})\ + \ (x_{t}-Ax_{t-1})^{T}\ P^{-1} \ (x_{t}-Ax_{t-1})}{dx_{t}} ... ...(3) 0=dxtd(zt−Cxt)T R−1 (zt−Cxt) + (xt−Axt−1)T P−1 (xt−Axt−1)......(3)
从公式(3)可得 ( C T R − 1 C + P − 1 ) x t = z t T R − 1 C + P − 1 A x t − 1 (C^{T}R^{-1}C+P^{-1})x_{t}=z_{t}^{T}R^{-1}C+P^{-1}Ax_{t-1} (CTR−1C+P−1)xt=ztTR−1C+P−1Axt−1
得到 x t = ( C T R − 1 C + P − 1 ) − 1 ( z t T R − 1 C + P − 1 A x t − 1 ) x_{t}=(C^{T}R^{-1}C+P^{-1})^{-1}(z_{t}^{T}R^{-1}C+P^{-1}Ax_{t-1}) xt=(CTR−1C+P−1)−1(ztTR−1C+P−1Axt−1)
应用矩阵的求逆定理(Inversion Lemma),可得
( C T R − 1 C + P − 1 ) − 1 = P − P C T ( R + C P C T ) − 1 C P (C^{T}R^{-1}C+P^{-1})^{-1}=P-PC^{T}(R+CPC^{T})^{-1}CP (CTR−1C+P−1)−1=P−PCT(R+CPCT)−1CP
因此定义卡尔曼增益(Kalman Gain): K = P C T ( R + C P C T ) − 1 K=PC^{T}(R+CPC^{T})^{-1} K=PCT(R+CPCT)−1 (最好参考下概率机器人)
得到 x t ^ = A x t − 1 + K ( z t − C A x t − 1 ) \hat{x_{t}}=Ax_{t-1}+K(z_{t}-CAx_{t-1}) xt^=Axt−1+K(zt−CAxt−1), 这里 K = P C T R − 1 − K C P C T R − 1 K=PC^{T}R^{-1}-KCPC^{T}R^{-1} K=PCTR−1−KCPCTR−1,点击看具体推导。
同时更新状态的协方差,需要用增益来更新: P ^ t = P − K C P \hat{P}_{t}=P-KCP P^t=P−KCP
举一个形象的例子,就是这个球位置的例子,从t-1时刻到t时刻,球正在从左往右移动。未来位置的估计可以从给定t-1时刻后x在t的概率得出 p ( x t ∣ x t − 1 ) p(x_{t}|x_{t-1}) p(xt∣xt−1),这个分布比较分散,因为运动模型并不可靠,这种分散是运动模型的噪声分布及状态分布的协方差 A P t − 1 A T + Σ m AP_{t-1}A^{T}+\Sigma_{m} APt−1AT+Σm共同作用的结果。观测的估计是一个协方差为 C P t C T + Σ o CP_{t}C^{T}+\Sigma_{o} CPtCT+Σo且均值比运动模型大的分布,协助 p ( x t ∣ x t − 1 ) p(x_{t}|x_{t-1}) p(xt∣xt−1)变为 p ( x t ) p(x_{t}) p(xt), 同时还限制了不确定性。

2.4 非线性变化(Non-Linear Variations)
扩展卡尔曼滤波器(extended Kalman filter)
在一个非线性动态系统中,状态转移方程状态的函数,因此预测模型的变化将显得较为困难。可微的方程可以通过在当前时刻线性化来简化这个过程。这个雅克比矩阵表示了这个矩阵的导数,但它无法表示一些高阶的特性,如果在未来一个时间步长中,状态没有巨大的变化,线性逼近就是一个可行的追踪状态分布变化的方法。
线性状态方程: p ( x t ∣ x t − 1 ) = N ( A x t − 1 , A P t A T + Σ m ) p(x_{t}|x_{t-1})=N(Ax_{t-1},AP_{t}A^{T}+\Sigma_{m}) p(xt∣xt−1)=N(Axt−1,APtAT+Σm)
对于非线性形式的状态方程,我们可以从线程状态方程改写为:
p ( x t ∣ x t − 1 ) = N ( f ( x t − 1 ) , ∂ f ∂ x t − 1 P t − 1 ∂ f T ∂ x t − 1 + Σ m ) p(x_{t}|x_{t-1})=N(f(x_{t-1}),\frac{\partial{f}}{\partial{x_{t-1}}}P_{t-1}\frac{\partial{f^{T}}}{\partial{x_{t-1}}}+\Sigma_{m}) p(xt∣xt−1)=N(f(xt−1),∂xt−1∂fPt−1∂xt−1∂fT+Σm)
在非线性状态方程中,我们使用非线性函数取代状态转移矩阵进行状态变换。实际上,在对预测协方差的计算中,雅克比矩阵取代了状态转移矩阵,同样的,卡尓曼增益(kalman gain)也被重写。
线性状态方程中的卡尔曼增益: K = P C T ( R + C P C T ) − 1 K=PC^{T}(R+CPC^{T})^{-1} K=PCT(R+CPCT)−1
非线性状态方程中的卡尔曼增益: K = P ∂ h T ∂ x ( R + ∂ h T ∂ x P ∂ h T ∂ x ) − 1 K=P\frac{\partial h^{T}}{\partial x}(R+\frac{\partial h^{T}}{\partial x}P\frac{\partial h^{T}}{\partial x})^{-1} K=P∂x∂hT(R+∂x∂hTP∂x∂hT)−1, 其中 ∂ h T ∂ x \frac{\partial h^{T}}{\partial x} ∂x∂hT为观测方程的雅克比矩阵。
雅克比矩阵是对 t t t时刻的点 x x x计算的,最终的跟踪状态的更新形式和线性系统非常相似,扩展卡尔曼滤波器是一个自然的想法,用来在可微的运动和观测模型下保留高斯分布的概念。
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
overall update(整体的更新为)
x t ^ = f ( x t − 1 ) + K ( z t − h ( f ( x t ) ) ) \hat{x_{t}}=f(x_{t-1})+K(z_{t}-h(f(x_{t}))) xt^=f(xt−1)+K(zt−h(f(xt)))
P t ^ = P − K ∂ h ∂ x P \hat{P_{t}}=P-K\frac{\partial h}{\partial x}P Pt^=P−K∂x∂hP
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
