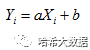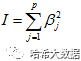【python+机器学习（4）】多维数据的特征选取（Ridge&&Lasso）
欢迎关注哈希大数据微信公众号【哈希大数据】
在之前我们介绍了直接使用线性回归进行波士顿房价的预测，但是预测准确率仅有60%左右。预测准确率不高一方面是我们未对数据进行一定的预处理（包括归一化和标准化等），这样不能确保在使用优化方式时，对不同特征参数起到同样的影响。 其次是未深入挖掘数据特征间关系，比如当原始数据某些特征与目标值不具有线性关系时，不应当纳入训练模型中。而且数据特征之间可能存在共线性等其他问题，不完全适合使用线性回归模型进行拟合。
因此，本节我们将介绍Ridge Regression（岭回归）和Lasso Regression（拉索回归），进行波士顿房价数据集中的特征选取和共线性问题的处理，从而更加准确的构建模型实现房价预测。
算法理论介绍
机器学习机制回顾
在之前Linear Regression普通线性回归的应用中（忘记的小伙伴可拉到文末查看线性回归详情内容），我们的输入数据是具有13个特征属性的波士顿房价数据集。
回归模型的构建就是实现这13个特征属性值的线性加权之和，用于与实际的房价进行拟合。
机器学习是如何得到权值呢？是通过定义的一个损失函数，实现将训练数据代入我们模型的预测房价和真实房价的差的平方，然后再将这些平方求和，即普通最小二乘法。
通过一定的理论推导可以得知权值系数实际为（特征属性值的广义逆）：
但是，直接使用普通的线性回归模型，当训练样本数量过少，甚至少于样本维数（仅有12条房屋数据），这样将导致特征数据矩阵无法求逆，则不能完成参数a的估计；其次如果样本特征中存在大量相似的特征（即样本属性之间存在共线性关系），将会导致很多权重所代表的意义重复，使原本简单高效的模型复杂化。
因此希望可以对参数a的计算时提供某种约束（增加一个惩罚因子），只保留具有共线性的一个特征属性值，而实现特征数据的缩减同时解决过拟合的问题，岭回归和拉索回归恰好可以解决该问题。
下面来详细了解一下岭回归和拉索回归的相关理论和python实现。
岭回归 Ridge
在出现普通线性回归无法解决的问题时，可以在原来加一个小扰动值λI
，其中I为对角矩阵
，可以对特征属性的权重计算进行一定约束，形象的称加入的对角矩阵I为岭。当λ越大，惩罚约束作用就越大，而原始数据对回归求取参数的作用就会减小，λ为0时也就是普通的线性回归算法。如果给λ指定一个合适的值，就能在一定意义上解决过拟合的问题（原先过拟合的特别大或者特别小的参数会被约束到正常取值但不会为零）。可以通过多次调试寻找较优的λ值，也就是当λ调整到获取的参数值稳定时即可。
因此岭回归可以初步解决特征权值参数a的动态调整（普通线性回归是无偏估计的唯一值），进而缓解过拟合的问题（尽可能找到不同 特征与目标值的具体关系）。
拉索回归 Lasso
岭回归可以动态调整特征属性的权重参数，进而使得模型更加契合实际情况，充分解释不同特征对目标值的影响力，但是其只能将具有线性相关的相似特征属性的权重降低却不能完全剔除。
拉索回归与岭回归类似也是加入了一个扰动项，其使用的惩罚项对角矩阵而是可以实现特征选择的收缩惩罚性：
，可以保证当λ充分大时可以把某些特征属性的权重精确地收缩到0，也就是在模型中剔除了该特征属性，从而从大量特征数据中挑选出。该方法的两大好处：一方面剔除噪声特征（也就是房价不受其影响的特征），其次可以消除具有线性相关关系的不同属性（会造成模型的不稳定，原因在之后做具体介绍）。
除此以外，岭回归中的约束因子λ需要手动调试，而在拉索回归算法中，可以实现λ参数的交叉验证，而寻找使得误差最小的λ的取值，使用交叉检验的训练方法可以进一步提高模型的科学性和准确性。
python实现
Ridge python同样使用scikit-learn库中的包实现该算法，岭回归算法实现的部分代码如下：
from sklearn.linear_model import Ridge
岭回归模型的导入
ridge = Ridge(alpha=float('{}'.format(i))).fit(house_price_train_X,house_price_train_y)# 默认的lamda的参数为i
岭回归模型训练的准确率
predict_result_ridge = ridge.predict(house_price_test_X)
predict_result_ridge1 = ridge.score(house_price_train_X, house_price_train_y)
predict_result_ridge0 = ridge.score(house_price_test_X, house_price_test_y)
print('岭回归惩罚参数为 {} ，训练集的准确率:'.format(i),predict_result_ridge1)
print('岭回归惩罚参数为 {} ，测试集的准确率:'.format(i), predict_result_ridge0)
普通拉索回归算法实现的部分代码如下：
普通拉索回归模型的导入
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=np.float('{}'.format(i)) ,max_iter=1000000).fit(house_price_train_X, house_price_train_y) # 默认的lamda的参数为i
拉索模型训练的准确率
predict_result_lasso = lasso.predict(house_price_test_X)
predict_result_lasso1 = lasso.score(house_price_train_X, house_price_train_y)
predict_result_lasso0 = lasso.score(house_price_test_X, house_price_test_y)
print('拉索回归惩罚参数为 {} ，训练集的准确率:'.format(i), predict_result_lasso1)
print('拉索回归惩罚参数为 {} ，测试集的准确率:'.format(i), predict_result_lasso0)
print('拉索回归惩罚参数为 {}，使用的特征属性有：{}'.format(i,np.sum(lasso.coef_ != 0))
交叉验证的拉索回归算法实现的部分代码如下：
实现交叉检验拉索回归模型的导入
from sklearn.linear_model import LassoCV
lasso_cv = LassoCV(alphas=np.logspace(-3,1,2,50) ,max_iter=1000000).fit(house_price_train_X, house_price_train_y) # 默认的lamda的参数为i
交叉检验拉索模型训练的准确率
predict_result_lasso_cv = lasso_cv.predict(house_price_test_X)
predict_result_lasso_cv1 = lasso_cv.score(house_price_train_X, house_price_train_y)
predict_result_lasso_cv0 = lasso_cv.score(house_price_test_X, house_price_test_y)
print('交叉检验拉索回归 训练集的准确率:', predict_result_lasso_cv1)
print('交叉检验拉索回归 测试集的准确率:', predict_result_lasso_cv0)
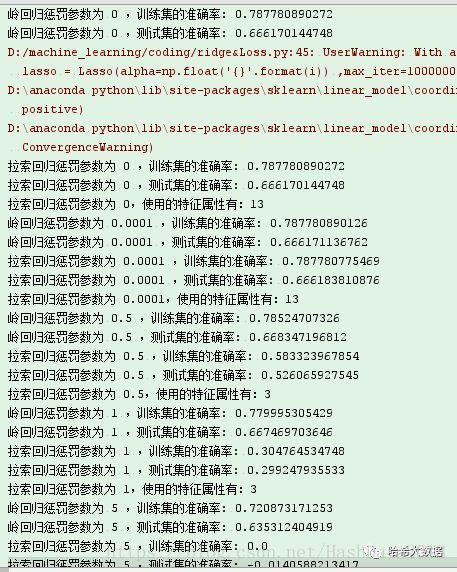
预测对比结果
1、当设置惩罚参数为0时会提示建议使用回归模型。2、当惩罚参数不同时，lasso算法选数据特征属性个数是不同的。3、如果惩罚参数设置过大，则无法进行预测。4、也因数据自身特征，三种方式的预测准确率相差不大。可以提示我们在训练不同数据时，要针对性的选用不同模型。（源码请直接通过给后台发消息获取哦！）
