动态规划------学习笔记

递归函数有n个参数，就定义一个n维的数组
数组的下标是递归函数参数的取值范围
数组元素的值是递归函数的返回值
这样就可以从边界值开始，逐步填充数组
相当于计算递归函数值的逆过程

动归解题的一般思路

1.将原问题分解为子问题

子问题和原问题形式相同或类似，只不过规模变小了，子问题解决，原问题即解决

子问题一旦求出就会被保存，所以每个子问题只需解一次

2.确定状态

一个状态对应一个或多个子问题，所谓某个状态下的值就是这个

3.确定一些初始状态（边界状态）的值

以数字三角形为例，初始初始状态就是底边数字，只就是底边数字值

4.确定状态转移方程

由已知推未知

能用动态规划解决问题的特点

1.问题具有最优子结构性质

2.无后效性

 

01背包问题，不同的物品只有一件

完全背包问题，不同的物品有无穷多个

 

一般的递归求斐波那契数列如果说对计算的结果不进行储存的话会造成大量的重复计算

换一张图就可以看出来

---

例题1： 

 我们来看这么一道题，有一个数列，我们做的是从这列数中选择出几个数使得他们的值最小，选出的数也是有要求的，他们不能使相邻的数

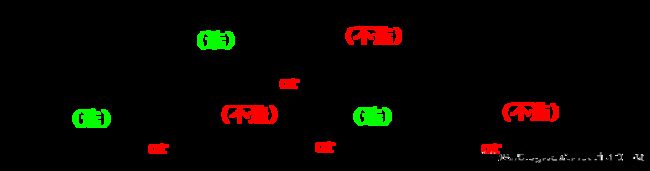
用动态规划的方法，咱们从最后的一个数开始看，然后看这个数的状态，他只有两种状态，选与不选

递归边间：
OPT(0)=arr[0]
OPT(1)=max(arr[0],arr[1])

下面我们来看代码怎么实现

递归形式：

#include
using namespace std;
int arr[7]={1,2,4,1,7,8,3};
int rec_opt(int arr[],int i){//rec表示递归 
	if(i==0){
		return arr[0];
	}
	else if(i==1){
		return max(arr[0],arr[1]);
	}
	else{
		int A=rec_opt(arr,i-2)+arr[i];
		int B=rec_opt(arr,i-1);
		return max(A,B);
	}
}

int main(){
	cout<

程序的运行过程是这样的：

很短，就是这个样子

接下来我们看看非递归的形式怎么写

这位UP主说递归不是最好的方法，虽然说递归比一定会慢，可以建立备忘来解决，主要原因是会爆调用栈

非递归形式就是把函数转化为数组

#include
using namespace std;
int arr[7]={1,2,4,1,7,8,3};
int main(){
	int opt[7]={0};
	opt[0]=arr[0];
	opt[1]=max(arr[0],arr[1]);
	for(int i=2;i<7;i++){
		int A=opt[i-2]+arr[i];
		int B=opt[i-1];
		opt[i]=max(A,B);
	}
	cout<

 

---

 例题2：

熟能生巧，我们再来看一道题

还是给出一个数列，然后再给出一个数，看从这一个数列中取出一个或多个数，它们之和能否组成这个数

 和上一题的方法一样，对每个数的状态分为选这个数和不选这个数

我们同样可以把程序的操作过程画出来

我们再来看程序的出口（递归边界）

if(s==0) return true;
if(i==0) return arr[0]==s;
if(arr[i]>s) return Subset(arr[i-1],s);

解释一下，s代表的是要凑的数

 递归形式：

#include
using namespace std;

int arr[7]={3,34,4,12,5,2,1};
int rec_subset(int arr[],int i,int s){
	if(s==0){
		return true;
	}
	else if(i==0){
		return arr[0]==s;
	} 
	else if(arr[i]>s){
		return rec_subset(arr,i-1,s);
	}
	else{
		int A=rec_subset(arr,i-1,s-arr[i]);
		int B=rec_subset(arr,i-1,s);
		return A||B;
	}
}


int main(){
	cout<

非递归形式：（貌似还有一点问题，头痛，明天再看）

#include
using namespace std;

int arr[7]={3,34,4,12,5,2,1};
int dp_subset(int arr[],int s){
	int subset[7][s];
	for(int i=0;i<7;i++){
		subset[i][0]=1;
	}
	for(int i=0;is){
				subset[i][s]=subset[i-1][s];
			}
			else{
				int A=subset[i-1][s-arr[i]];
				int B=subset[i-1][s];
				subset[i][s]=(A||B); 
			}
		}
	} 
	for(int i=0;i<7;i++){
		for(int j=0;j