NOIP2017提高组DAY2题解

T1：奶酪

考察知识：搜索，并查集，枚举

算法难度：XX 实现难度：XX

分析：这道题我当年考试用的dfs，没有处理最后20%的情况，得了80分。下面讲解用并查集解决此题。

显然我们可以用并查集合并连通的洞，只需要进行枚举就可以了

然后我们继续枚举两个不同的洞，如果一个与下边界相交，一个与上边界相交，且在同一个集合里，说明有解；如果枚举完都没有找到解，说明无解。

时间复杂度：

代码：

#include
#include
#include
#include
using namespace std;
const int maxn=1005;
int f[maxn];
void init(int n){
    for(int i=1;i<=n;i++) f[i]=i;
}
int find(int x){
    return x==f[x]?x:f[x]=find(f[x]);
}
void merge(int x,int y){
    int fx=find(x),fy=find(y);
    if(fx!=fy) f[fx]=fy;
}
int T;
long long n,h,r,x[maxn],y[maxn],z[maxn];
long long dis(int i,int j){
    return ceil(sqrt((x[i]-x[j])*(x[i]-x[j])+
    (y[i]-y[j])*(y[i]-y[j])+(z[i]-z[j])*(z[i]-z[j])));
}
bool check(){
    cin>>n>>h>>r;
    init(n);
    for(int i=1;i<=n;i++) cin>>x[i]>>y[i]>>z[i];
    for(int i=1;i=h)
        if(find(i)==find(j)) return true;
    return false;
}
int main(){
    scanf("%d",&T);
    while(T--) printf("%s\n",check()?"Yes":"No");
    return 0;
}

T2：宝藏

考察知识：状态压缩，搜索，模拟退火，骗分

算法难度：XXXX 实现难度：XXX+

分析：这道题解法众多，但是骗分方法绝对是简单而且高效的。（去年考试我连树和图是什么都不知道，所以这道题我就输出输入值乘以一个常数，得了5分，T_T）

下面介绍一个随机化多重贪心方法，简单而且正确率超高。（我第一次看到该方法是在：题解 P3959 【宝藏】）

先介绍一个函数random_shuffle（随机函数），格式和sort差不多，对a[1]...a[n]随机打乱：

random_shuffle(a+1,a+n+1);

对于这道题，我们先得出一个宝藏挖掘顺序，然后按照顺序用贪心解决，获得当前顺序可以得到的最小花费，然后我们多次随机化挖掘顺序，在所有结果中取最小值即可。

至于重复的贪心次数大家可以在时间效率与正确性中间自己把握。

代码：（比较易懂，就不加注释了）

#include
#include
#include
#include
using namespace std;
const int inf=0x3f3f3f3f;
int n,m,g[13][13],a[13],dep[13],ans=inf;
int calc(){
    int ret=0;
    memset(dep,0,sizeof(dep));
    dep[a[1]]=1;
    for(int i=2;i<=n;i++){
        int to=a[i],now_v=inf,pre=0;
        for(int s=1;s<=n;s++) if(dep[s]&&g[s][to]

T3：列队

考察知识：树状数组，平衡树，模拟

算法难度：XXXX+ 实现难度：XXXX+

分析：去年考试最后20分钟开始写这道题的暴力，然而0分。

我们先分析一下列队的移动：

如图，我们发现如果红色那块要出队，共需要移动四块。我们发现种序列的移动可以用Splay来维护，仔细观察发现，水平有n行可能需要移动，而竖直只可能发生在最后一列，所以我们维护 n+1 个Splay，维护n个长度为m-1的序列，1个长度为n的序列。

每次移动时（x,y），我们需要将水平第x个Splay中第y个元素删除，将竖直Splay的第x个元素删除，然后将删除的两个元素分别插入这两个Spaly就可以了。

但是如果我们直接开Splay，空间不够，注意到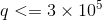，我们可以用Spaly维护区间，每次删除时需要将区间一分为三，然后将中间元素删除并更新剩余两个区间。

理解了上面的思路后，剩下的就基本是Spaly的基本操作+变形了，考察大家对Splay的熟练程度了。

注意：

1.最大值会超过int，所以区间用long long储存

2.Spaly常数比较大，可能会有部分点超时。（vijos：可以AC；洛谷：不开O2 95 开O2 AC）

3.当y==m只修改竖直方向上的Spaly

代码：

#include
#include
#include
#include
using namespace std;
#define ll long long
const int N=300005,maxn=2400005;
int ch[maxn][2],fa[maxn],sz[maxn],now,cnt[maxn];
ll L[maxn],R[maxn];
struct Splay{
	int rt;
	Splay(){rt=0;} 
	int NewNode(ll l,ll r){//新建节点 
		now++,L[now]=l,R[now]=r;
		sz[now]=cnt[now]=r-l+1;
		return now;
	}
	void init(ll l,ll r){rt=NewNode(l,r);}//空树的初始化 
	#define upd(x) cnt[x]=R[x]-L[x]+1
	#define pushup(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]
	#define DB_ for(int i=0;i<=now;i++) \
	printf("[%lld,%lld]%d<- %d[%lld,%lld] ->%d[%lld,%lld]\n", \
	L[ch[i][0]],R[ch[i][0]],ch[i][0],i,L[i],R[i],ch[i][1],L[ch[i][1]],R[ch[i][1]]);\
	puts("----------------")
	int chk(int x){return x==ch[fa[x]][1];}
	void rotate(int x){
		int y=fa[x],z=fa[y],k=chk(x),w=ch[x][k^1];
		ch[y][k]=w,fa[w]=y;
		ch[z][chk(y)]=x,fa[x]=z;
		ch[x][k^1]=y,fa[y]=x;
		pushup(y),pushup(x);
	}
	void splay(int x,int goal=0){
		while(fa[x]!=goal){
			int y=fa[x],z=fa[y];
			if(z!=goal){
				if(chk(x)==chk(y)) rotate(y);
				else rotate(x);
			} rotate(x);
		} if(!goal) rt=x;
	}
	void insert(ll l,ll r){//插入到序列末尾 
		if(rt==0) {init(l,r);return;}
		int cur=rt;
		while(ch[cur][1]) cur=ch[cur][1];
		ch[cur][1]=NewNode(l,r),fa[ch[cur][1]]=cur;
		splay(ch[cur][1]);
	}
	int beside(int x,int pre){//求一个子序列的前驱/后继 
		splay(x);
		int cur=ch[x][pre^1];
		if(!cur) return 0;
		while(ch[cur][pre]) cur=ch[cur][pre];
		return cur;
	}
	ll kth_and_del(int k,bool exit_=false){//查找第k大的数并从子序列中删除 
		int cur=rt;
		if(sz[rt]==1){//只有一个数 
			rt=0;//变为空树 
			return L[cur];
		}
		while(true){//kth
			if(ch[cur][0]&&k<=sz[ch[cur][0]])
			  cur=ch[cur][0];
			else if(k>sz[ch[cur][0]]+cnt[cur])
			  k-=sz[ch[cur][0]]+cnt[cur],cur=ch[cur][1];
			else break;
		}
		k-=sz[ch[cur][0]];
		if(exit_) return L[cur]+k-1;//仅查询不删除，用于查看中间结果 
		int pre=beside(cur,1),nxt=beside(cur,0);//del
		if(pre) splay(pre);
		if(nxt) splay(nxt,pre);
		if(L[cur]==R[cur]){//子序列只有一个数，直接删除 
			if(nxt) ch[nxt][0]=0;//特别注意！分类讨论不存在前驱或后继的情况 
			else if(pre) ch[pre][1]=0;
			else rt=0; 
			if(pre) sz[pre]--;
			if(nxt) sz[nxt]--;
			return L[cur];
		}
		else{
			ll ret=L[cur]+k-1;
			if(k==1) L[cur]++,upd(cur),sz[cur]--;
			else if(k==cnt[cur]) R[cur]--,upd(cur),sz[cur]--;
			else{//将子序列一分为三，并删除中间的数 
				ch[cur][0]=NewNode(L[cur],L[cur]+k-2); 
				fa[ch[cur][0]]=cur;
				L[cur]+=k,upd(cur),pushup(cur);
				splay(cur);
			}
			return ret;
		}
	}
}s[N];
int n,m,q;
void build(){
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++)
	  s[i].init((ll)(i-1)*m+1,(ll)i*m-1);
	s[0].init((ll)m,(ll)m);
	for(int i=2;i<=n;i++)
	  s[0].insert((ll)i*m,(ll)i*m);
}
void solve(){
	int x,y;
	ll last=(ll)n*m;
	while(q--){
		scanf("%d%d",&x,&y);
		if(y!=m){
			ll t1=s[x].kth_and_del(y),t2=s[0].kth_and_del(x);
			printf("%lld\n",last=t1);
			s[x].insert(t2,t2);
			s[0].insert(t1,t1);
		} else if(x!=n){
			ll t=s[0].kth_and_del(x);
			printf("%lld\n",last=t);
			s[0].insert(t,t);
		}else{
			printf("%lld\n",last);
		}
//		DB_; //用于查看当前各Splay节点情况 
	}
}
int main(){
	build();
	solve();
	return 0;
}