随机数字生成器（RNG）和Hash函数组合武器背后的黑暗秘密

　　本文主要的参考文献为：
1. 游戏编程中的数学——随机数字生成（RNG）的黑暗秘密
2. A Primer on Repeatable Random Numbers

　　文章题目之所以叫“黑暗秘密”，只是我觉得这个名字比较酷=。=然而并没有涉及到太多背后的数学原理，只是对其分布作了一些有趣的实验~
　　进入正题，在游戏编程当中，总是会不可避免地用上随机数生成器（简称 RNG,Random Number Generators ）。但是， RNG 这东西可不是随便用的，你需要根据实际应用的场景进行一些合理的选择。比方说，随机数是否允许重复？
　　我相信，绝大多数情况下我们是不希望生成的随机数出现重复的，比方说，在一些消除类游戏当中，

开心消消乐游戏截图

　　出现的游戏方块都是利用随机数产生的，然而开发者并不希望游戏出现太多重复的游戏方块，这样会影响开发者预期的玩家得分流程，甚至出现 bug 。总的来说，什么场景下我们不希望重复随机数的出现？最主要的一点便是：

• 不希望玩家能够重新审视同一世界。例如，在一些沙盒游戏当中，当你从特定的种子创建出某个世界时， 如果再次使用了相同的种子，则会再次获得相同的世界。

　　我们提到了“种子”这个概念。一般来说，种子可以是 int、string 类型的数据，也可以是其它类型的数据，以此作为输入获得一个随机的输出。种子最大的特点便是：相同的种子会得到相同的随机数序列，但当种子发生轻微变化时，得到的随机数序列便与原来的相比大相径庭。
　　在本文中，我将研究两种不同方法产生的随机数分布：随机数生成器 RNG 和 Hash 函数，并尝试将其结合起来。其中，利用C# 产生数据，利用 Matlab 绘制图形。具体代码可以参见我的 Github 项目： RNG 与 Hash 函数相关代码。

RNG

　　产生随机数最常用的方法便是使用随机数生成器（简称 RNG ）。 许多编程语言（如本文使用的C#）都提供了随机数的生成方法。
　　随机数生成器根据初始种子产生一系列随机数。 在许多面向对象的语言中，随机数生成器通常是一个经种子初始化的对象，然后可以重复调用该对象的方法来产生随机数。

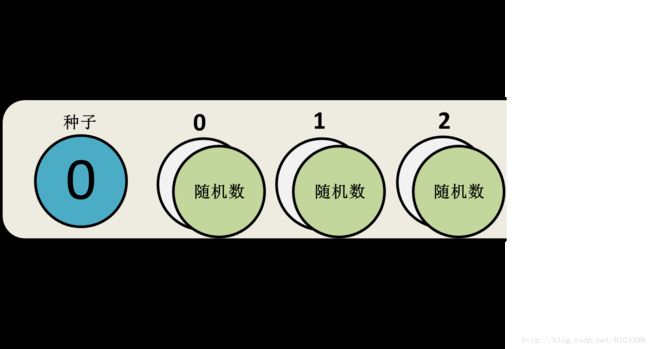
　　在这种情况下，我们可以利用C# 的 Random 类提供的 Next() 方法得到0~1000000之间的随机整数值。之所以选择1000000作为最大值，主要是为了图形绘制的方便，后面可以看到，我会将每一个随机数映射到一个边长为100单位的立方体上的某个格点上。
　　如下所示的图像，包含由种子0生成的100000个随机数。其中，每个随机数表示一个立方体上的一个位置，以行序为主。立方体每一个格点的像素值范围为(0,0,0)→(1,1,1)，初始 RGB 值为(0,0,0)，每当有一个随机数落在该处时，该处像素点的 R、G、B 三个通道值均会自增0.1，直到达到1为止。

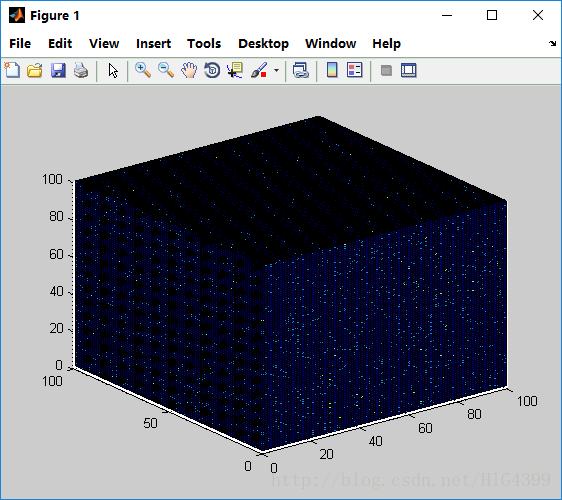
　　这里需要注意的是如果没有第一个和第二个随机数，你就不能得到第三个随机数。 就其性质而言， RNG 使用先前的随机数产生每个随机数作为计算的一部分。 因此我们研究 RNG ，研究的对象都应该是一个随机序列。

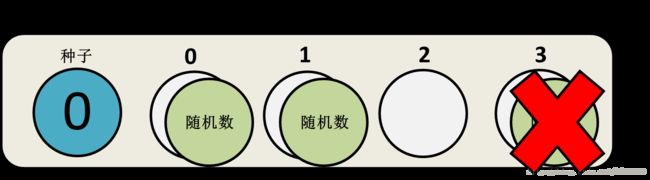
　　这样一来，使用 RNG 就会有一个明显的缺点：如果你仅需要一个特定的随机数（比如序列中的第100个随机数），那么你就需要调用 Next() 方法26次，并使用最后一个数字，但这是非常不方便的。

为什么你需要序列中的特定随机数？

　　如果你一次性生成所有的东西，你可能不需要一个序列中的特定随机数。然而存在这样一种情形：
　　假设你的世界中有三个部分： A,B 和 C 。其中 A 部分使用0号种子生成的随机数序列前100个随机数生成。然后玩家进入 B 部分，使用第101-200个随机数生成。此时部分 A 被销毁以释放内存。最后玩家进入 C 区，使用第201-300个随机数生成。同样地，部分 B 被销毁。
　　然而，如果玩家现在又回到 B 部分，那么为了使部分 B 看起来不变，应该使用与第一次相同的100个随机数生成。然而因为 A 已经被销毁，所以我们无法直接得到第101-200个随机数，需要利用0号种子重新生成整个随机数序列。

不能只使用具有不同种子值的随机数生成器吗？

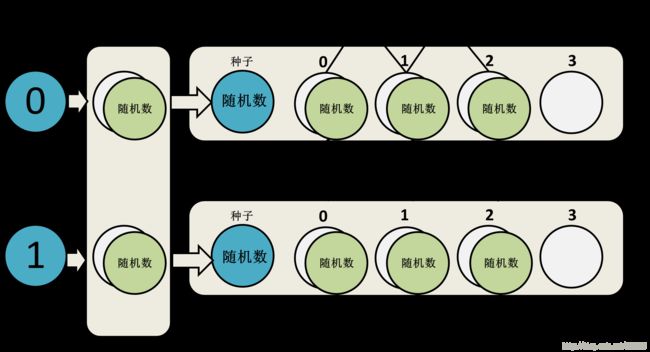
　　需要澄清的是，这是对于 RNG 的一个非常常见的误解。 事实是，尽管同一序列中的不同随机数字可以说是相互独立的，但是来自不同随机序列的相同索引的数字彼此之间并不是独立的，它们之间可能呈现某种分布。

　　所以如果你有100个序列，并从每个序列中取出第 i(i≥1) 个随机数数，那么这100个随机数就不会是相互独立的随机数。 它们之间可能会服从某种分布。
　　不妨做一下实验看看~我将0到99999这100000个数字作为 RNG 的种子，得到100000个随机序列，分别取每一个随机序列的第一个随机数将其映射到一个边长为100单位的立方体上，如下图所示：

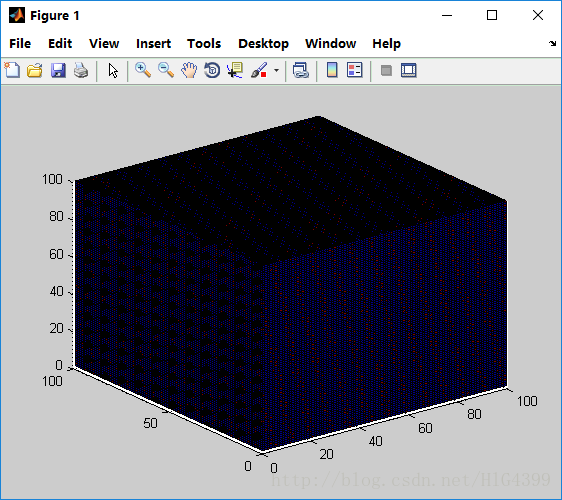
　　显然此时的模式分布已经不再均匀，相反呈现出一个直线族！如果分布已知，那还不如直接用一个线性函数去进行随机数的生成23333……
　　显然，这样一种使用具有不同种子值的随机数生成器的操作是不大可行的。最起码，我们也应该保证输出在肉眼上看起来是随机的，因为玩家通常不会认真跟你去计算具体的随机数分布……想象一下，如果你通过上述操作生成随机数创建坐标，用于在一块平地上种植树木。现在，所有的树木都被被排成一条直线，其余的平地部分都是空的！相信这会是一件十分尴尬的事囧。
　　为了解决这个问题，我觉得我们有必要引入哈希函数。

Hash 函数

　　通常， Hash 函数是将把原空间的一个数据集映射到像空间的一个函数。且像空间一般要比原空间更小，以方便处理。
　　与随机数生成器 RNG 不同，使用 Hash 函数生成随机数是不需要随机序列的，即可以按任意顺序得到随机数，只要你提供了一个输入~

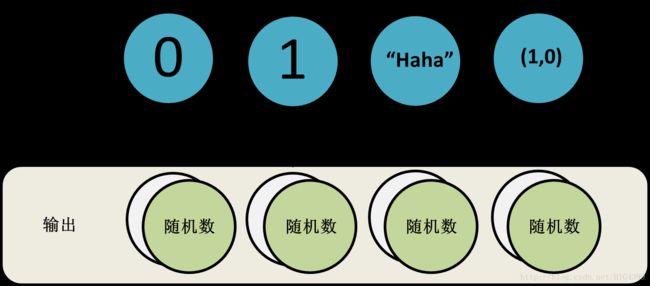
　　 Hash 函数的设计是非常讲究的，其中核心的设计原则便是降低碰撞的概率，常用的做法便是降低 card(X)card(X′) 的大小，其中 X 是原空间， X′ 是像空间， card(X) 表示 X 的势， card(X′) 表示 X′ 的势，没学过实变函数的没关系=。=就理解为集合的数量即可。显然，当 card(X)=card(X′) 的时候我们可以实现无碰撞。
　　有一篇文章对于哈希表的数学原理是讲得十分透彻的，有兴趣的同学可以看看：哈希表之数学原理。
　　偷懒了一下，我仅仅测试了两种十分经典的 Hash 函数： MD5 与 SHA1 函数。

• MD5 ：这可能是最著名的 Hash 函数之一了。 在生成随机数时，我们通常只需要一个32位 int 值作为返回值，而 MD5 会返回一个更大的散列值，其中大部分我们只是扔掉。尽管如此，我觉得 MD5 还是值得测试一波的。
• SHA1 ：这也是一个十分经典的 Hash 函数，通常返回20字节（160位）的数据摘要。由于它产生的数据摘要的长度更长，因此更难以发生碰撞，因此也更为安全，但也因此在一定程度上降低了它的运算速度。

　　我将0到99999这100000个数字分别作为 MD5 与 SHA1 函数的输入，得到100000个随机数，依旧是将其映射到一个边长为100单位的立方体上。如下两图是 MD5 与 SHA1 函数的测试结果：

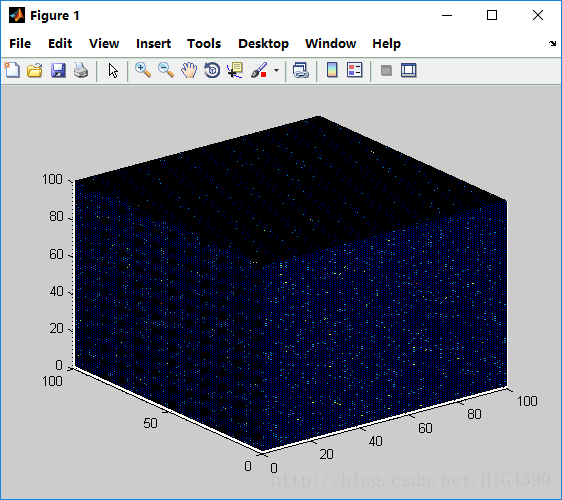
MD5 测试结果

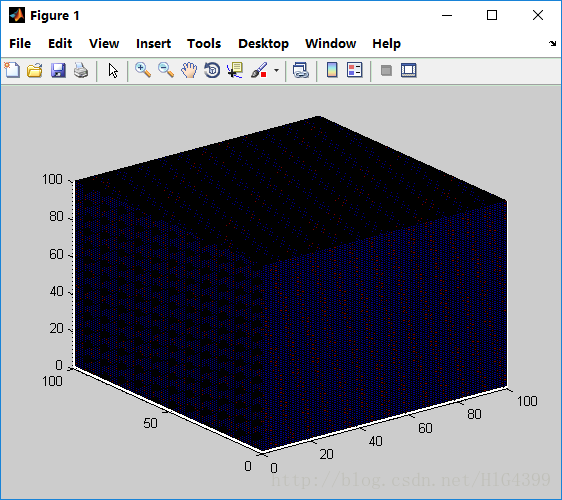
SHA1 测试结果

　　容易看出， MD5 函数生成的数字具有良好的随机性，而 SHA1 函数生成的数字却再次呈现出一个直线族的分布！！！总能与直线扯上关系，细思极恐……相信背后一定有深刻的数学原理，若有时间，会再深入研究一波~
　　然而，这并不能说明 SHA1 函数不适用于随机数的生成。因为在实际操作当中，每生成一个随机数就得调用一次 Hash 函数，这太消耗性能了。。。我们不妨将 RNG 与 Hash 函数结合起来，这便有了下面的讨论。

RNG 与 Hash 函数的合体

　　 RNG 与 Hash 函数也可以结合使用。 我们前面已经说到，一个明智的方法是使用不同种子的随机数生成器，但为了使输出结果在肉眼上看起来尽可能地随机，种子（例如在创建迷宫世界时，种子可以是迷宫位置坐标）必须首先通过 Hash 函数的处理而非直接使用，否则会使输出结果呈现出直线族分布。

　　再做一波实验，分别测试一下经 MD5 函数和 SHA1 函数处理的随机数生成器效果，如下两图所示：

经 MD5 函数处理的随机数生成器效果

经 SHA1 函数处理的随机数生成器效果

　　可以看出，使用经 MD5 函数和 SHA1 函数处理的随机数生成器进行随机数的生成时，随机数的分布已经能够呈现出不错的随机性，这是满足我们的预期目标的。

总结

　　总而言之，如果你需要一堆随机数，最简单的方法就是使用随机数生成器（ RNG ），例如 C＃ 中的 System.Random 类。 为了使所有的随机数相互之间是随机的，要么只使用一个随机序列（即用一个种子初始化，但是当需要序列中的特定随机数时它便显得不是很方便，具体原因文中已经解释），要么使用多个种子，但是在使用这堆种子之前需要先通过一个 Hash 函数进行处理。个人还是比较推荐第二种方法的~