CNN基本问题

基本理解

CNN降低训练参数的2大法宝

局部感受野、权值共享
局部感受野：就是输出图像某个节点（像素点）的响应所对应的最初的输入图像的区域就是感受野。
权值共享：比如步长为1，如果每移动一个像素就有一个新的权值对应，那么太夸张了，需要训练的参数爆炸似增长，比如从32x32的原图到28x28经过convolve的图，如果后者的每一个像素对应前面的一个参数，那参数实在是多。权值共享就是将每次覆盖区域的图像所赋给的权值都是卷积核对应的权值。就是说用了这个卷积核，则不管这个卷积核移到图像的哪个位置上，图像的被覆盖区域的所赋给的权值都是该卷积核的参数。

从全连接到CNN经历了什么？

演化进程： 全连接——->（全连接加上局部感受野了进化成)局部连接层———->(局部连接层加上权值共享了)卷积神经网络。
比如简单点就用2维图像，100x100 到 100x100，那么如果全连接第一层所有点都与第二层所有点相连，就有 108 个连接，加上局部感受野了。不精确的计算(不考虑边缘带来的问题)，假设局部为3x3大小。那么第一层的每个点都与3x3的局部有连接，就是说，有 104∗3∗3 个连接，才能得到下一层100x100(假设加了padding)。此时局部连接网络的权值数和连接数是一样的，都是 104∗3∗3 ， 如果再加上权值共享，形成卷积神经网络，那么这 104 个点不是每个都有自己独立的3x3个权值，而是这 104 共享这3x3个点。因此最终卷积网络的权值只有3x3大小！

更多信息可以参考 这里， 对于局部感受野和权值共享写的很详细。其实 Convolutional layers are technically locally connected layers. To be precise, they are locally connected layers with shared weights.

啥叫feature map啊？

同一种滤波器卷积得到的向量组合。一种滤波器提取一种特征，下图使用了6种滤波器，进行卷积操作，故有6层feature map.

C1层用了6个5x5的卷积核，这里的步长为1，因此每个feature map是(32-5+1)x(32-5+1)=28x28.

CNN训练的参数是啥啊？

其实就是卷积核！！！当然还有偏置。
比如上面的6个5x5的卷积核的训练参数是6x(5x5+1)，当然咯，每个卷积核对应的偏置自然是不同的。
某篇论文的卷积网络表示：
Fw(∂I)=Wn∗Fn−1(∂I)+bn , n = 3
Fn(∂I)=σ(Wn∗Fn−1(∂I)+bn) , n = 1,2
F0(∂I)=∂I , n = 0

可以看出啊，总共三层卷积网络，然后第一层第二层都是直接将输入的进行卷积，这里的 Wn 就是权值参数，也就是卷积核。外加一个偏置 bn .当然每传入下一层要一个激活函数，这里选用的是双曲正切。

卷积和到底怎么卷积的？？

其实是这样的。一般CNN的卷积是二维卷积，这时候你可能要问了，为啥二维啊，明明添加层的时候代码都写到4维了。一般是这样的，假设前一层的特征是 C∗H∗W , 那么我们要用什么卷积核呢？ 用 C∗N∗h∗w 的。显然h，w就是有些论文中说的spatial size。 那么第二个参数 N 就是我们要输出的维度大小。而第一个参数 C 就是要和需要进行卷积的特征的通道数保持一致。你可能会问，为啥是这样的呢？显然每次计算时是用卷积核在spatial 上进行移动，每次对应的是 C∗h∗w 与 C∗N∗h∗w 进行计算。
重点：
为啥说用的是二维卷积。因为这个实质上是 C∗h∗w 的向量 p 与 C∗h∗w 的向量 q 进行内积！！。 N 代表我们分别用 q1,q2...qN 与p进行內积，所以就会得到N个“垂直方向”的点，当在spatial上完成移动之后，就会有N个feature map了。
可以这样认为，其实也没啥高级的，比如一幅图片是三维的3*H*W，那么显然在我们有H*W*3个点来描述这幅图像。我们就取一个spatial location的点吧。一个位置有3个数进行描述。有时候我们需要升维，就是希望用更多的值来描述这个点，这样可能会得到更多的关于这幅图片的特征。然后我们用 3∗5∗h∗w 进行卷积。这时候我们得到的每个位置是5个值 r1,...,r5 来描述了。并且这5个值的每个值 ri 都是其原来位置的周围（包括自身）9个点的值的加权和( ri=∑m∑nwmnrmn ,大概这样写吧，懂了意思就行。)，这样可以说我们通过第一个卷积核的3*3个参数与对应的位置卷积得到了第一个值，第二个值也是通过第二个卷积核的3*3个参数与对应的位置卷积从而得到，… 仔细看刚才说的，通过第一个卷积核的3*3个参数与对应的位置卷积得到了第一个值，因此需要 q 写的时候是 C∗N∗h∗w 。

究极总结

q 是 N 个卷积向量 qi ,每个是 qi 都是 C∗h∗w 大小。每个分别与相同大小的 p 的 C∗h∗w 进行点乘,是 C∗h∗w pair数字 对应相乘，再求和。然后进行 N 次。

如何计算训练的参数和连接？

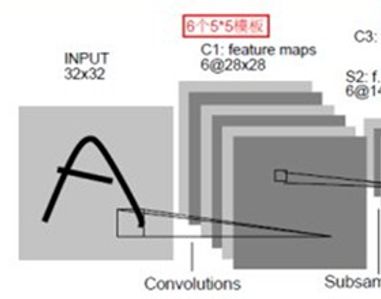
参数：从图可以看出，这个是用了6个filter，每个filter是5x5，所以这一层的参数是6x(5*5+1)，其实在大部分的代码实现中，都是直接去掉bias的，因为这个对结果没啥影响。但是本文还是加上了bias。
连接：经过convolve的图变成了(32-5+1)x(32-5+1)=28*28，有：(5*5+1)*(28*28)*6=122,304个连接。因为6个feature map，每个map有28*28个像素，而每个像素是通过5*5大小的filter经过卷积再加上偏置得到的。因此有这么多连接。

Pooling

就是将一块区域直接变成一个像素，不经过卷积核。一般有2种，max pooling和average pooling.主要是为了防止过拟合，减少训练参数。通过卷积后得到图像的特征，这是因为图像具有一种“静态性”的属性，这也意味着一个图像区域有用的特征极有可能在另一个区域同样适用。因此对于大图像，可以用聚合统计，通过average或是max pooling，可以得到低得多的维度，同事不容易过拟合。这种聚合操作就是pooling（池化）

如何计算感受野大小

1. 无padding情况：
   如果输入是 a∗a ，filter是 b∗b ,那么不加padding情况下，就会卷积后图像变小，变成 (a−b+1)∗(a−b+1) ，当计算感受野，就是计算这一层的输出的图像的像素点所对应的原图的像素点的个数。因此，如果我们走极端思想，我们假设经过 N 层的卷积，然后只输出一个像素点。那么就计算这个像素点的感受野。
   假设感受野是 X2 大小，然后根据公式，第一层是 (X−f1+1)∗(X−f1+1) ,因此有：
   X−(f1+f2+⋯+fN)+N=1 , 解出 X 即可。
   如：Image Super-Resolution Using Deep Convolution Networks, 就是SRCNN，SRCNN没有加入padding，它使用了三层，分别是9x9，1x1和5x5， X−(9+5+1)+3=1 ,得出 X=13 ,因此原文说
   On the whole, the estimation of a high resolution pixel utilizes the information of (9+5−1)2=169 pixels.

2. 有padding：
   额，其实有没有padding都是一样的，不会影响感受野大小。。着不用想也知道啊，用的方法同上。因为padding只是增加了边缘区域的像素点，可是filter利用的点的个数还是一样的，只不过经过padding后，利用了一些特殊的像素点（比如zeros padding)罢了。
   比如在Accurate Image Super-Resolution Using Very Deep Convolution Networks，也就是VDSR中，它有20层的weight layers，每层都是用3x3的filters，并且有padding的。第一层的感受野就是3x3，第二层就是5x5，第D层就是 (2D+1)×(2D+1) 。从下面可以推出：
   X−(3+3+⋯+3)D个+D=1

stride的含义

这个就是下采样参数，当然了conv层，则stride=1；如果是pooling层，该pooling层的大小是2x2，那么就stride=2了。

其他一些东西

带 μ 的权值更新方式

一般来说，标准的BP更新是：

W(t)=W(t−1)−η∂E∂W

但是有一种Momentum的更新方式：

Δw(t+1)=η∂Et+1∂w+μΔw(t)

这里的 μ 就是momentum参数。
η 就是学习率。

这里的 λ 就是正规化项regularization term，也称为权重衰减项(weight decay),这个主要是防止过拟合的，就是很多权重变成0，增加稀疏性。

附带：三种激活函数的对比图，我觉得我画的还是挺漂亮的，所以拿过来-_-//,不会有什么意见吧。。

x = [-3:0.01:3];
plot(x,tanh(x),'r',x,1./(1+exp(-x)),'c--',x,max(0,x),'m-.');
legend('Tanh','Sigmoid','ReLu');
grid on;