数据特征分析技能—— 相关性检验
数据特征分析技能—— 相关性检验
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度
一般常用四种方法:
- 画图判断
- pearson(皮尔逊)相关系数
- sperman(斯皮尔曼)相关系数
- Cosine similarity (余弦相关系数)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
% matplotlib inline绘制图形判断
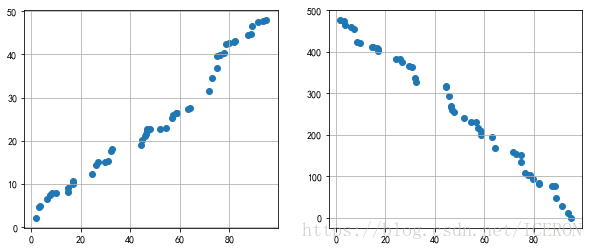
一般对于强相关性的两个变量,画图就能定性判断是否相关
data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
# 创建三个数据:data1为0-100的随机数并从小到大排列,data2为0-50的随机数并从小到大排列,data3为0-500的随机数并从大到小排列,
fig = plt.figure(figsize = (10,4))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1, data2)
plt.grid()
# 正线性相关
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1, data3)
plt.grid()
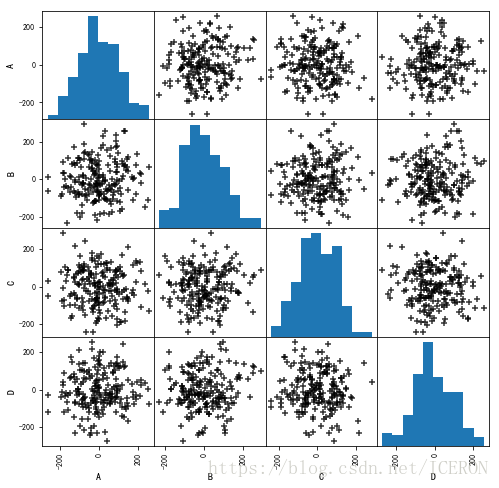
# 负线性相关# (2)散点图矩阵初判多变量间关系
data = pd.DataFrame(np.random.randn(200,4)*100, columns = ['A','B','C','D'])
pd.plotting.scatter_matrix(data,figsize=(8,8),
c = 'k',
marker = '+',
diagonal='hist',
alpha = 0.8,
range_padding=0.1)
data.head()| A | B | C | D | |
|---|---|---|---|---|
| 0 | 83.463300 | 108.208281 | -16.441879 | -69.039664 |
| 1 | -114.341786 | -176.341932 | -64.282506 | 54.378911 |
| 2 | -108.781464 | 116.223511 | 11.996554 | 4.445215 |
| 3 | -124.358401 | -74.357458 | -46.089528 | -73.539092 |
| 4 | 87.330398 | 205.767923 | 59.964420 | 137.955811 |
pearson(皮尔逊)相关系数
要求样本满足正态分布
- 两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商,其值介于-1与1之间
公式:
协方差:sxy=1n−1∑nk=1(xk−x¯)(yk−y¯) s x y = 1 n − 1 ∑ k = 1 n ( x k − x ¯ ) ( y k − y ¯ )
标准差:sx=1n−1∑nk=1(xk−x¯)2−−−−−−−−−−−−−−−√ s x = 1 n − 1 ∑ k = 1 n ( x k − x ¯ ) 2
皮尔逊相关系数:sxysxsy=∑nk=1(xk−x¯)(yk−y¯)∑nk=1(xk−x¯)2√∑nk=1(yk−y¯)2√ s x y s x s y = ∑ k = 1 n ( x k − x ¯ ) ( y k − y ¯ ) ∑ k = 1 n ( x k − x ¯ ) 2 ∑ k = 1 n ( y k − y ¯ ) 2
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据
u1,u2 = data['value1'].mean(),data['value2'].mean() # 计算均值
std1,std2 = data['value1'].std(),data['value2'].std() # 计算标准差
print('value1正态性检验:\n',stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正态性检验:\n',stats.kstest(data['value2'], 'norm', (u2, std2)))
print('------')
# 正态性检验 → pvalue >0.05
data['(x-u1)*(y-u2)'] = (data['value1'] - u1) * (data['value2'] - u2)
data['(x-u1)**2'] = (data['value1'] - u1)**2
data['(y-u2)**2'] = (data['value2'] - u2)**2
print(data.head())
print('------')
# 制作Pearson相关系数求值表
r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print('Pearson相关系数为:%.4f' % r)
# 求出r
# |r| > 0.8 → 高度线性相关 value1 value2
0 0.438432 0.486913
1 2.974424 0.663775
2 4.497743 1.417196
3 5.490366 2.047252
4 6.216346 3.455314
------
value1正态性检验:
KstestResult(statistic=0.07534983222255448, pvalue=0.6116837468934935)
value2正态性检验:
KstestResult(statistic=0.11048646902786918, pvalue=0.1614817955196972)
------
value1 value2 (x-u1)*(y-u2) (x-u1)**2 (y-u2)**2
0 0.438432 0.486913 1201.352006 2597.621877 555.603052
1 2.974424 0.663775 1133.009967 2345.549928 547.296636
2 4.497743 1.417196 1062.031735 2200.319086 512.612654
3 5.490366 2.047252 1010.628854 2108.181383 484.479509
4 6.216346 3.455314 931.020494 2042.041746 424.476709
------
Pearson相关系数为:0.9937
# Pearson相关系数 - 算法
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据
data.corr()
# pandas相关性方法:data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson| value1 | value2 | |
|---|---|---|
| value1 | 1.000000 | 0.996077 |
| value2 | 0.996077 | 1.000000 |
Sperman秩相关系数
皮尔森相关系数主要用于服从正太分布的连续变量,对于不服从正太分布的变量,分类关联性可采用Sperman秩相关系数,也称 等级相关系数
计算方法:
- 对两个变量按照取值大小从小到大编秩,Rx代表Xi的秩次,Ry代表Yi的秩次
- 如果两个变量秩次一样,则秩次为(index1+index2)/ 2
- di = Rx -Ry
公式:
ρs=1−6∑d2in(n2−1) ρ s = 1 − 6 ∑ d i 2 n ( n 2 − 1 )
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
'每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据
data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)
print(data)
print('------')
# “智商”、“每周看电视小时数”重新按照从小到大排序,并设定秩次index
data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2
print(data)
print('------')
# 求出di,di2
n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Sperman秩相关系数为:%.4f' % rs)
# 求出rs 智商 每周看电视小时数
0 106 7
1 86 0
2 100 27
3 101 50
4 99 28
5 103 29
6 97 20
7 113 12
8 112 6
9 110 17
------
智商 每周看电视小时数 range1 range2
1 86 0 1 1
8 112 6 9 2
0 106 7 7 3
7 113 12 10 4
9 110 17 8 5
6 97 20 2 6
2 100 27 4 7
4 99 28 3 8
5 103 29 6 9
3 101 50 5 10
------
智商 每周看电视小时数 range1 range2 d d2
1 86 0 1 1 0 0
8 112 6 9 2 7 49
0 106 7 7 3 4 16
7 113 12 10 4 6 36
9 110 17 8 5 3 9
6 97 20 2 6 -4 16
2 100 27 4 7 -3 9
4 99 28 3 8 -5 25
5 103 29 6 9 -3 9
3 101 50 5 10 -5 25
------
Sperman秩相关系数为:-0.1758
# spearman相关系数 - 算法
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
'每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据
data.corr(method='spearman')
# pandas相关性方法:data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson| 智商 | 每周看电视小时数 | |
|---|---|---|
| 智商 | 1.000000 | -0.175758 |
| 每周看电视小时数 | -0.175758 | 1.000000 |