最大流之Ford-Fulkerson方法详解及实现
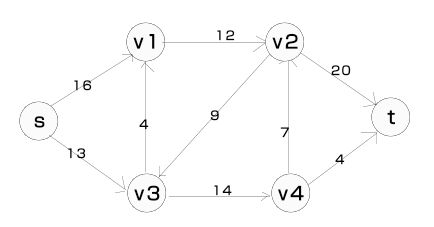
最大流问题常常出现在物流配送中,可以规约为以下的图问题。最大流问题中,图中两个顶点之间不能同时存在一对相反方向的边。
边上的数字为该条边的容量,即在该条边上流过的量的上限值。最大流问题就是在满足容量限制条件下,使从起点s到终点t的流量达到最大。在介绍解决最大流问题的Ford-Fulkerson方法之前,先介绍一些基本概念。
1. 残存网络与增广路径
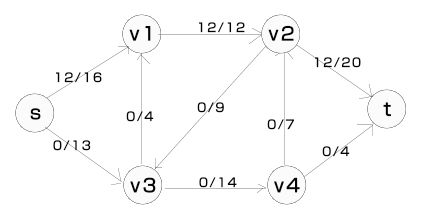
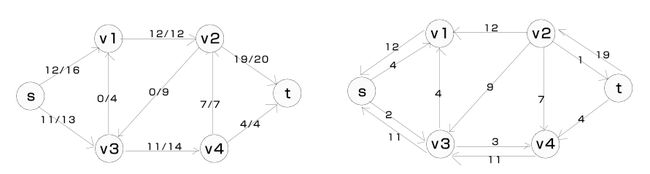
根据图和各条边上的流可以画出一幅图的残存网络如下所示。左图为流网络,右图为残存网络,其中流网络中边上的数字分别是流量和容量,如10/12,那么10为边上的流量,12为边的容量。残存网络中可能会存在一对相反方向的边,与流网络中相同的边代表的是流网络中该边的剩余容量,在流网络中不存在的边代表的则是其在流网络中反向边的已有流量,这部分流量可以通过“回流”减少。例如,右图残存网络中,边
残存网络描述了图中各边的剩余容量以及可以通过“回流”删除的流量大小。在Ford-Fulkerson方法中,正是通过在残存网络中寻找一条从s到t的增广路径,并对应这条路径上的各边对流网络中的各边的流进行修改。如果路径上的一条边存在于流网络中,那么对该边的流增加,否则对其反向边的流减少。增加或减少的值是确定的,就是该增广路径上值最小的边。
2. Ford-Fulkerson方法
Ford-Fulkerson方法的正确性依赖于这个定理:当残存网络中不存在一条从s到t的增广路径,那么该图已经达到最大流。这个定理的证明及一些与其等同的定理可以参考《算法导论》。
Ford-Fulkerson方法的伪代码如下。其中
Ford-Fulkerson
for ∈ E
.f = 0
while find a route from s to t in e
m = min(.f, ∈ route)
for ∈ route
if ∈ f
.f = .f + m
else
.f = .f - m Ford-Fulkerson有很多种实现,主要不同点在于如何寻找增广路径。最开始提出该方法的Ford和Fulkerson同学在其论文中都是使用广度优先搜索实现的,其时间复杂度为O(VE),整个算法的时间复杂度为O(VE^2)。
下面我给出一个应用Bellman-Ford计算单源最短路径的算法实现寻找一条增广路径,对于用邻接矩阵表示的图来说,该实现的时间复杂度为O(V^3),对于用邻接表表示的图来说,时间复杂度则为O(VE)。
// 寻找增广路径
int findRoute(int **e, int vertexNum, int *priorMatrix, int s,int t)
{
s--; t--;
int *d = (int *)malloc(sizeof(int)*vertexNum);
// initialize
for (int i = 0; i < vertexNum; i++)
{
d[i] = 0;
priorMatrix[i] = -1;
}
d[s] = 1;
// 反复用边做松弛操作,将更新为
for (int k = 0; k < vertexNum; k++)
{
for (int i = 0; i < vertexNum; i++)
{
for (int j = 0; j < vertexNum; j++)
{
if (d[j] == 0)
{
d[j] |= (d[i] & (*((int*)e + i*vertexNum + j) > 0));
if (d[j] == 1)
{
priorMatrix[j] = i;
}
}
}
}
}
if (d[t] == 0) return 0;
int min = INT_MAX;
int pre = priorMatrix[t];
while (pre != -1)
{
if (min > *((int*)e + pre*vertexNum + t))
{
min = *((int*)e + pre*vertexNum + t);
}
t = pre;
pre = priorMatrix[t];
}
return min;
} 下面给出根据图和流网络计算残存网络的代码。
// 计算残存网络
void calculateENet(int **c, int vertexNum, int **f, int **e)
{
for (int i = 0; i < vertexNum; i++)
{
for (int j = 0; j < vertexNum; j++)
{
int a = *((int*)c + i*vertexNum + j);
if (a != 0)
{
*((int*)e + i*vertexNum + j) = a - *((int*)f + i*vertexNum + j);
*((int*)e + j*vertexNum + i) = *((int*)f + i*vertexNum + j);
}
else
{
*((int*)e + i*vertexNum + j) = 0;
}
}
}
}
/**
* Ford-Fulkerson方法的一种实现
* @param c 二维矩阵,记录每条边的容量
* @param vertexNum 顶点个数,包括起点和终点
* @param s 起点编号,编号从1开始
* @param t 终点编号
* @param f 输出流网络矩阵,二维矩阵,记录每条边的流量
*/
void Ford_Fulkerson(int **c, int vertexNum, int s, int t, int **f)
{
int *e = (int *)malloc(sizeof(int)*vertexNum*vertexNum); // 残存网络
int *priorMatrix = (int *)malloc(sizeof(int)*vertexNum); // 增广路径的前驱子图
// initialize
for (int i = 0; i < vertexNum;i++)
{
for (int j = 0; j < vertexNum; j++)
{
*(f + i*vertexNum + j) = 0;
}
}
while (1)
{
calculateENet(c, vertexNum, (int **)f, (int **)e); // 计算残存网络
int min;
if ((min = findRoute((int **)e, vertexNum, priorMatrix, s, t)) == 0) // 寻找增广路径及其最小流值
{
break;
}
int pre = priorMatrix[t - 1];
int next = t - 1;
while (pre != -1) // 按增广路径更新流网络
{
if (*((int*)c + pre * vertexNum + next) != 0)
{
*((int*)f + pre * vertexNum + next) += min;
}
else
{
*((int*)f + next * vertexNum + pre) -= min;
}
next = pre;
pre = priorMatrix[pre];
}
}
}3. 测试及效果
下面给出用于测试的代码。
void testFord()
{
int c[6][6] = { 0, 16, 13, 0, 0, 0,
0, 0, 0, 12, 0, 0,
0, 4, 0, 0, 14, 0,
0, 0, 9, 0, 0, 20,
0, 0, 0, 7, 0, 4,
0, 0, 0, 0, 0, 0 };
int f[6][6];
Ford_Fulkerson((int **)c, 6, 1, 6, (int **)f);
for (int i = 0; i < 6; i++)
{
for (int j = 0; j < 6; j++)
{
int flow = f[i][j];
if (flow != 0)
{
printf("%d -> %d : %d\n", i + 1, j + 1, flow);
}
}
}
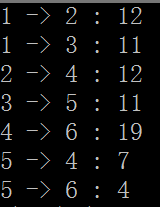
}运行结果如下,其中1为顶点s,5为顶点t,2~5依次为顶点v1、v2、v3和v4。
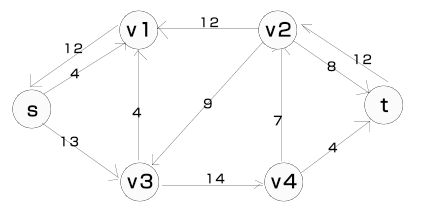
流网络和残存网络如下所示,其中左图为流网络,右图为残存网络。
我们可以看到残存网络中的确已经不存在一条从s到t的路径了。此时Ford-Fulkerson方法的循环应该终止,最大流量为各边的流量相加之和,即76。
完整的程序可以看到我的github项目 数据结构与算法
这个项目里面有本博客介绍过的和没有介绍的以及将要介绍的《算法导论》中部分主要的数据结构和算法的C实现,有兴趣的可以fork或者star一下哦~ 由于本人还在研究《算法导论》,所以这个项目还会持续更新哦~ 大家一起好好学习~