OpenCV-识别细胞图中的细胞总数

背景：

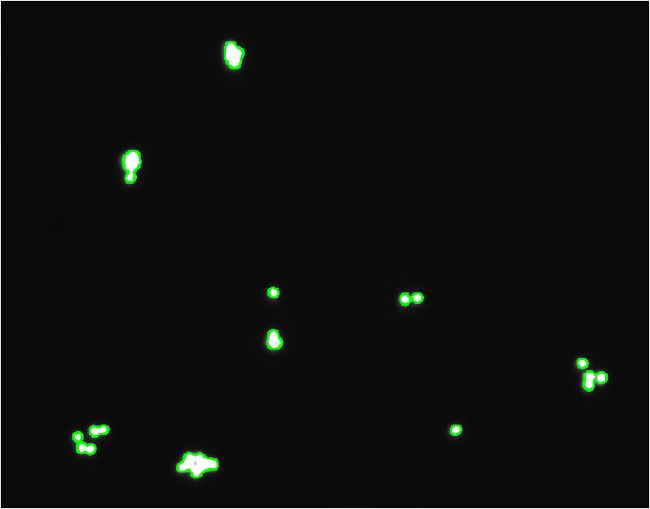
最近在学习OpenCV,在CV群里有个人问了一个问题，就是个了一幅图片，识别里面的细胞，并且识别出细胞的总个数。原图如下所示：

图中白色的细胞。

分析：

1、首先要定位到细胞，就是确定细胞的位置。

这个很容易办到，进行二值化就可以得到清晰的黑白轮廓，然后通过寻找连通域可以圈出图中细胞的位置。

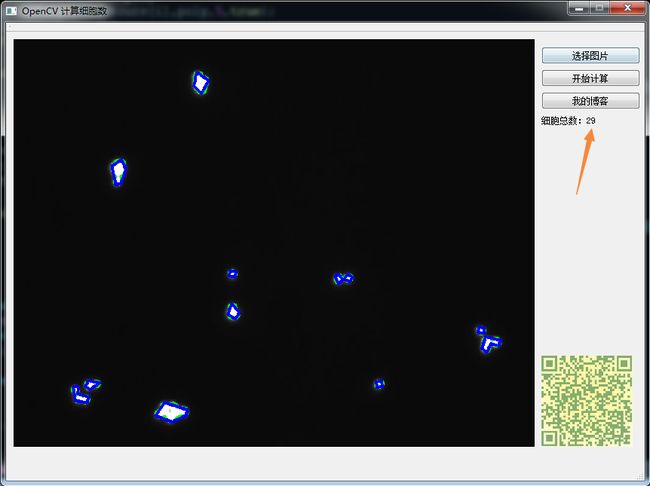
2、识别定位到细胞的总个数。

这个就有点难办了。

难点1：细胞重叠了怎么算。

难点2：怎么才能识别为单个细胞，怎么算重叠呢。

实现：

1、定位细胞位置：

a.转灰度图后二值化，使得黑白更加明显。代码如下：

    // to gray
    cv::cvtColor(cellImage,result1d,CV_BGR2GRAY);
    // threshold
    cv::threshold(result1d,result1d,128,255,cv::THRESH_BINARY);

效果图如下：

b.寻找连通域

寻找连通域，并计算连通域的个数，同时把连通域边界用绿色标记，代码如下：

    // find contours and got contours sum
    cv::findContours(result1d,contours,CV_RETR_EXTERNAL,CV_CHAIN_APPROX_NONE);
    int ctsSum = contours.size();
    // draw all contours // draw polygon in cell finded and count polygon-edges to count cell num
    for(int i=0;i

效果图如下：

2、识别细胞的总个数：

a.确定每一个连通域（上图中的每一坨）的个数

本来想用面积来计算每一坨被圈住里面的细胞个数，但是前提条件是要知道单个细胞的面积大小，才可以用总的面积除以单个细胞的面来计算每一坨的细胞个数。所以首先要解决这个问题，怎么知道单个细胞的面积大小勒！

b.获得单个细胞的面积

经过我的认真观察可以发现一个规律，重叠处的细胞，比如：，这个细胞坨大概有五个，可惜TMD他们重叠了，但是可以发现连接他们的端点可以获得一个五边形，【那么机会来了，我们只要通过用多边形包罗这一坨，得到的多边形边数就可以认为是细胞的个数咯】，所以可以把上面那一坨包罗成这样，可以看到他是个5边形。代码如下：

    for(int i=0;i poly;
        cv::approxPolyDP(contours[i],poly,5,true);
        cv::polylines(cellImage,poly,true,cv::Scalar(250,0,0),3);
        }
    }

效果图如下：

但是，我们从图中可以发现，单个细胞和两个重叠在一起的细胞也被包罗为四边形【所以可以这么认为：只有大于4的多边形才能算数】，那么计算单个细胞面积的方法就得出来了：通过计算边数大于4的连通域的总面积除以总的边数就可以粗略的得到单个细胞面积。再次分析可以知道重叠的细胞大概有1/5被忽略掉所以我们可以加上这五分之一的补偿得到总面积，所以计算公式如下：

单个细胞的近似面积 = {边数大于4的边数的总面积 + 边数大于4的边数的总面积 * （1/5）} / 总边数

代码如下：

    for(int i=0;i 4){
            cell_cnt += poly.size(); // >4的边数的多边形 就是 （认为有效的）细胞数
            area += fabs(cv::contourArea(contours[i])) + fabs(cv::contourArea(contours[i]))*0.2;// 加上重叠处
        }
    }

到此，得到单个细胞的面积，和计算出边数大于4的细胞数。

c.得到边数为4或者小于4的细胞数

用边数小于或者等于4的连通域的面积除以单个细胞的近似面积就可以近似得到该连通域包含的细胞数了，比如两个细胞重叠也会被包罗成四边形，但是通过除以单个细胞的面积，那么就可以得到2，那么，该连通域包含的细胞就是2咯。系不系啊！SO，聪明的你应该已经想到方法了！代码如下：

    for(int i=0;i poly;
        cv::approxPolyDP(contours[i],poly,5,true);
        if(poly.size() == 4){
            if(fabs(fabs(cv::contourArea(contours[i])) - per_cell_area) < 20){
                cell_cnt++;// 细胞面积接近单个细胞的面积 判断为1个
            }else{
                cell_cnt += static_cast(fabs(cv::contourArea(contours[i]))/per_cell_area);// 否则可能为2个或者4个情况
            }

        }else if(poly.size() < 4){
            cell_cnt += 3;// 一般只有3个的情况 就是三角形
        }else{
            if(fabs(fabs(cv::contourArea(contours[i]))/poly.size() - per_cell_area) < 20){
                cell_cnt += poly.size();// 分裂成单个细胞与单个细胞接近 判断为多边形的个数
            }else{
                cell_cnt += static_cast(fabs(cv::contourArea(contours[i]))/per_cell_area);// 否则就是意外情况 则用面积判断
            }
        }
    }

到此，我们就得到了细胞的总个数，结果非常精确，不信你自己数一数。结果图如下：

源码下载：

点击打开链接