算法与设计分析作业2(动态规划)

算法与设计分析作业2(动态规划)

1 Largest Divisible Subset

Given a set of distinct positive integers, find the largest subset such that every pair (Si,Sj) of elements in this subset satisfies:Si%Sj = 0 or Sj%Si = 0.

The optimal substructure and DP equation

首先将数组升序排序，这样我们就可以把较大的问题转换成较小的问题。dp[i]表示以dp[i]为最大数的符合要求子集的最大元素个数，max[i]表示到i位置为止符合要求子集的最大元素个数。因此该题可以将n个元素的符合要求的最大子集转变为前n-1个元素符合要求的最大子集(直至只剩下一个元素)。递推式为：

另外我们利用pre[]数组记录前一个可整除的值的下标，最后根据这些下标找到自己元素。

Pseudo-code

# @param {Integer[]} nums
# @return {Integer[]}
function largest_divisible_subset(nums)
      if nums.length==0 then return [] end  
      nums数组升序排序
      建立dp数组并填充1
      建立max数组并填充1
      建立pre数组并填充为自己的下标
      for i in 1...nums.length
        for j in 0...i
          if nums[i]%nums[j]==0 && dp[i]1
            dp[i]=dp[j]+1
            pre[i]=j
          end
        end
        max[i]=max(dp[i],max[i-1])
      end
      建立子集subset
        取max数组中第一个最大值的下标x
      while pre[x]!=x
        根据下标指示将元素nums[x]加入到子集subset中
        x=pre[x]
      end
      将最后一个元素nums[x]加入到子集subset中
      返回自己subset
end

Prove the correctness

首先该问题包含最优子结构的性质，我们可以将n个元素的符合要求的最大子集转变为前n-1个元素符合要求的最大子集(直至只剩下一个元素)。其次该问题包含重叠子性质，在解题过程中许多子问题需要重复计算，比如计算dp[3]是需要计算dp[2]+1,计算dp[4]需要计算dp[2]+1，那么dp[2]就是需要重复计算的，因此可以用”备忘录”将其记录。综上该题用动态规划是正确的。

The complexity of your algorithm

首先排序算法的复杂度为O(nlogn)，求dp过程中的循环次数为n*(n-1)/2，复杂度为O(n²)，最后回溯求子集的复杂度为O(n)，因此最后的时间复杂度为O(n²)。

2 Money robbing

A robber is planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

1. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
2. What if all houses are arranged in a circle?

The optimal substructure and DP equation

对于问题1，dp[i]表示从0~i家房子能抢到钱的最大数目，对于每一个房子，我们可以做一个决策，抢钱或者不抢钱。若是不抢钱，我们在该房子位置能抢到的最多钱就是前一个房子的能抢到的最多钱dp[i]=dp[i-1]，若是抢钱，我们在该房子位置能抢到的最多钱就是当前房子能抢到钱加上前二个房子能抢到的最多钱dp[i]=dp[i-2]+nums[i]。两种决策的最大值就是该房子位置能抢到的最多钱。因此递推式为：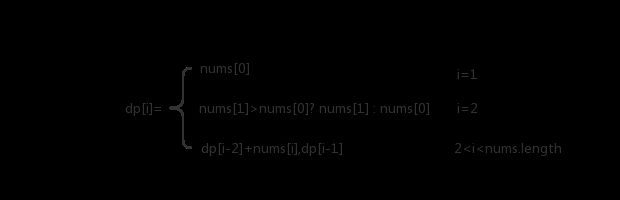

对于问题2，递推式是不变的，由于房子形成一个环，所以第一个房子和最后一个房子不能同时抢，所以只能抢第一个房子或者抢最后一个房子，因此我们只需要求0~nums.length-2号房子能抢到的最多钱和1~nums.length-1号房子能抢到的最多钱，两者比较求最大值。

Pseudo-code

# @param {Integer[]} nums
# @return {Integer}
# question 1：
function rob(nums)
    if nums.length==0 then return 0 end
    if nums.length==1 then return nums[0] end
    建立dp数组长度为length并填充值为0
    dp[0]=nums[0]
    dp[1]= nums[1]>nums[0]? nums[1] : nums[0]
    for i in 2...nums.length
        dp[i]=max(dp[i-2]+nums[i],dp[i-1])
    end
    return dp[nums.length-1]
end

# question 2：
# @param {Integer[]} nums
# @return {Integer}
function rob(nums)
    if nums.length==0 then return 0 end
    if nums.length==1 then return nums[0] end
    if nums.length==2 then return nums[1]>nums[0]? nums[1] : nums[0] end
    return max(robsub(nums,0,nums.length-2),robsub(nums,1,nums.length-1))
end

function robsub(nums,s,e)
    建立dp数组长度为e-s+1并填充值为0
    dp[0]=nums[s]
    dp[1]= nums[s+1]>nums[s]? nums[s+1] : nums[s]
    for i in 2...e-s+1
        dp[i]=max(dp[i-2]+nums[s+i],dp[i-1])
    end
    return dp[e-s]
end

Prove the correctness

首先该问题包含最优子结构的性质，求到第n个房子能抢到的最多钱包含到第n-2个房子的抢到最多钱和到第n-1个房子能抢到的最多钱。另外该问题也具有重叠子性质，大量子问题会重复计算，如求dp[5]需要计算dp[3],求dp[4]需要求dp[3]，因此dp[3]被重复计算。综上该问题可以用动态规划方法解。

The complexity of your algorithm

时间复杂度为O(n)。

4 Decoding

A message containing letters from A-Z is being encoded to numbers using the following mapping:
​ A : 1

​ B : 2

​ …

​ Z : 26
Given an encoded message containing digits, determine the total number of ways to decode
it.
For example, given encoded message “12”, it could be decoded as “AB” (1 2) or “L” (12). The number of ways decoding “12” is 2.

The optimal substructure and DP equation

dp[i]表示从字符0~i的字符串包含最多的编码种数。不考虑特殊情况，该题的递推式是dp[i]=dp[i-1]+dp[i-2]，因为一个数字可以表示一个编码，两个数字也有可能表示一个编码，所以dp[i]应该等于0~i-1的字符串包含的最多编码种数加上0~i-2的字符串包含的最多编码种数。但是考虑到一共只有26种基础编码加上特殊情况0，所以递推式可以表示为：

Pseudo-code

# @param {String} s
# @return {Integer}
fuction num_decodings(s)
    if s.length==0||s[0]=='0' then return 0 end
    if s.length==1 then return 1 end
    建立dp数组长度为s.length
    dp[0]=1
    if s[1] == '0'
        if s[0] > '2' || s[0] == '0'
            return 0
        end
        dp[1]=1
    elsif s[0..1].to_i >26
        dp[1]=1
    else
        dp[1]=2
    end
    for i in 2...s.length
        if s[i]=='0'
            if s[i-1] > '2'|| s[i-1] == '0'
                return 0
            end
            dp[i]=dp[i-2]
        elsif s[(i-1)..i].to_i >26
            dp[i]=dp[i-1]
        elsif s[i-1]=='0'
            dp[i]=dp[i-1]
        else
            dp[i]=dp[i-1]+dp[i-2]
        end
    end
    return dp[s.length-1]
end

Prove the correctness

首先该问题包含最优子结构的性质，求0~n的字符串包含最多的编码种数包含了求0~n-1的字符串包含最多的编码种数或0~n-2的字符串包含最多的编码种数。其次该问题包含重叠子性质，大量子问题会重复计算，如求dp[5]需要计算dp[4]或dp[3],求dp[4]需要求dp[3]或dp[2]，因此dp[3]被重复计算。综上该问题可以用动态规划方法解。

The complexity of your algorithm

时间复杂度为O(n)。

5 Frog Jump

A frog is crossing a river. The river is divided into x units and at each unit there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
If the frog’s last jump was k units, then its next jump must be either k−1,k, or k +1 units. Note that the frog can only jump in the forward direction.
Given a list of stones’ positions (in units) in sorted ascending order, determine if the frog is able to cross the river by landing on the last stone. Initially, the frog is on the first stone and assume the first jump must be 1 unit.

The optimal substructure and DP equation

dp[i] (i=pos|k<<11)表示当前pos位置前一次走k个单元有否可能到达最后一个单元。该题的作法是回溯法加上“备忘录（动态规划）”，由于单独使用回溯法会大量计算重复的子问题，因此每算出一个dp[n]将其记录，下次再算到dp[n]直接将其返回。

Pseudo-code

 # @param {Integer[]} stones
# @return {Boolean}
function can_cross(stones)
  建立hash表dp
  return can_cross2(stones,0,0,dp)
end

function can_cross2(stones,k,pos,dp)
  key = pos | k << 11
  if dp[key]!=nil then return dp[key] end
  if pos==stones.length-1 then return dp[key]=true end
  for i in pos+1...stones.length
    if stones[i]-stones[pos]>k+1 then return dp[key]=false end
    if stones[i]-stones[pos]1 then next end
    if can_cross2(stones,stones[i]-stones[pos],i,dp) then return dp[key]=true end
  end
  dp[key]=false
end 

Prove the correctness

首先该问题包含最优子结构的性质和重叠子性质，因此可以用动态规划解此题。

The complexity of your algorithm

时间复杂度为O(n*n)

6 Maximum profit of transactions

You have an array for which the i-th element is the price of a given stock on day i.
Design an algorithm and implement it to find the maximum profit. You may complete at most two transactions.
Note: You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

C++ Code

class Solution {
public:
    int maxProfit(vector<int>& prices) { 
        int len=prices.size();
        if(len==0) return 0;
        int *dp=new int[len];
        int *dp2=new int[len];
        memset(dp,0,len*sizeof(int));
        memset(dp2,0,len*sizeof(int));
        int min=prices[0];
        for(int i=1;i//dp[i]用来计算0~i进行一次交易获得的最大收益
            dp[i]=dp[i-1];
            if(prices[i]>min&&prices[i]-min>dp[i])
                dp[i]=prices[i]-min;
            if(min>prices[i])
                min=prices[i];
        }
        int max=prices[len-1];
        for(int i=len-2;i>=0;i--){ //dp2[i]用来计算从i~len-1进行一次交易获得的最大收益
            dp2[i]=dp2[i+1];
            if(max>prices[i]&&max-prices[i]>dp2[i])
                dp2[i]=max-prices[i];
            if(prices[i]>max)
                max=prices[i];
        }
        int maxPro=0;
        for(int i=0;i//dp[i]+dp2[i]的最大值即使两次交易所能获得的最大值
            if(maxProdelete []dp;
        delete []dp2;
        return maxPro;
    }
};

7 Maximum length

Given a sequence of n real numbers a1,…,an, determine a subsequence (not necessarily contiguous) of maximum length in which the values in the subsequence form a strictly increasing sequence.

C++ Code

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size()==0)
            return 0;
        int dp[nums.size()];
        dp[0]=1;
        int max=1;
        for(int i=1;i//dp[i]记录的是以d[i]为最后一个数的递增子序列的长度
            dp[i]=1;
            for(int j=0;jif(nums[i]>nums[j]&&dp[i]1){
                    dp[i]=dp[j]+1;
                }
            }
            if(max//max值代表最大递增子序列的长度
                max=dp[i];
        }
        return max;
    }
};