数据结构与算法 （9）：滑动窗口算法

数据结构与算法 （9）：滑动窗口算法

在算法题中，有一类题名曰：Sliding window（滑动窗口），其命名得益于其算法运行过程中，有一个显示或隐式存在的window(窗口).在解决某些问题上，可以起到降低时间复杂度为O(n)的效果。下面举两个例子来描述这种算法。

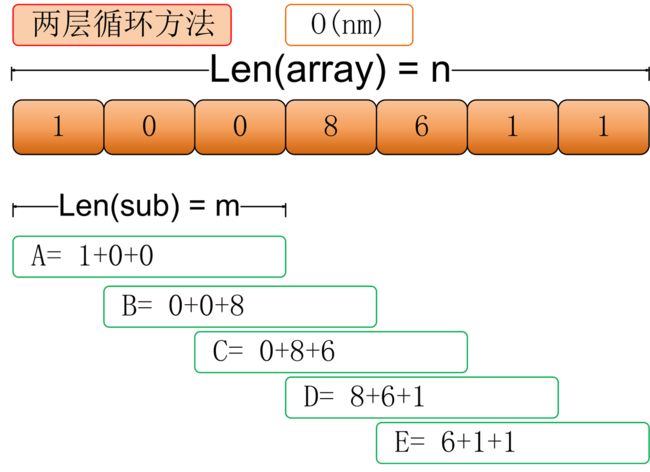
例子1：给定一组大小为n的整数数组，计算长度为m的子数组和的最大值

例如，数组为：array= {1,0,0,8,6,1,1}，m = 3
最大值为：8+6+1 = 15

直观上来说，我们可能会采用如下做法：

//此段代码引自：https://www.cnblogs.com/cdfive2018/p/10054563.html
int index = 0;// 记录最大子数组的索引，初始化
int maxSum = 0;// 记录最大子数组和，初始化

//求第一个maxSum 
for (int i = 0; i < m; i++) {
    maxSum += array[i];
}

for (int i = 1; i <= array.length - m; i++) {// 遍历所有子数组，求和并比较
    int curSum = 0;
    for (int j=0; j < m; j++) {// 计算当前子数组和
        curSum += array[i + j];
    }
    if (curSum > maxSum) {// 如果大于最大和，则记录
        maxSum = curSum;
        index = i;
    }
}

如果以这种方式，我们虽然可以求解到最大子数组和，以及其索引，但是需要o(mn)的时间复杂度，因为在求解过程中，我们用两个循环来遍历子数组。显然，这种时间复杂度是很高的。但如果我们把算法稍作修改，如下：

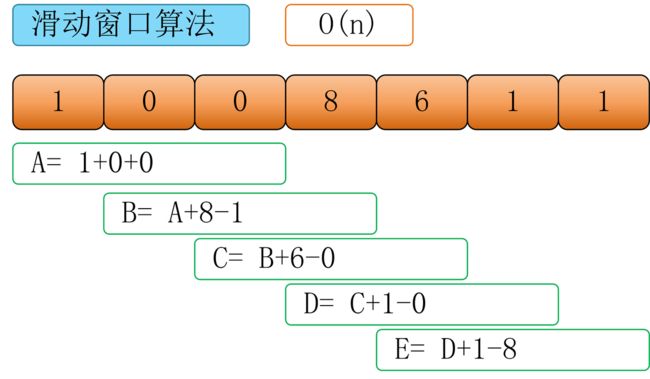
//此段代码引自：https://www.cnblogs.com/cdfive2018/p/10054563.html
int index = 0;// 记录最大子数组的索引
int maxSum = 0;// 记录最大子数组和

for (int i = 0; i < m; i++) {
    maxSum += array[i];
}

int curWindowSum = maxSum; //初始化窗口
for (int i = 1; i <= array.length - m; i++) // 从下个元素开始，即窗口向右滑动
    {
    curWindowSum = curWindowSum - array[i - 1] + array[m + i - 1]; // 减去失效值，加上最新值
    if (curWindowSum > maxSum) // 如果大于最大和，则记录
    {
        maxSum = curWindowSum;
        index = i;
    }
}

我们发现，经过简单的修改，这种算法同样能解决问题，并且时间复杂度为0(n).下面我们再举一个例子，详细说明滑动窗口算法的优势。

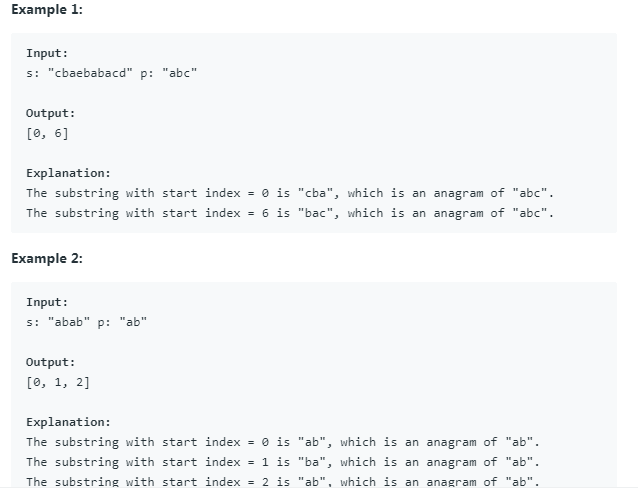
例子2：LeetCode 438. Find All Anagrams in a String

Given a string s and a non-empty string p, find all the start indices of p’s anagrams in s.

Strings consists of lowercase English letters only and the length of both strings s and p will not be larger than 20,100.

The order of output does not matter.

"""
此题要求：
    在s中找到能够成p的所有子串（字符位置连续，顺序可不一样，见example）,并返回满足要求的所有子串起始位置组成的列表。
    设 s 串长度为n , p串长度为 m 。
1.直观方法：
    主问题：我们可以通过两层循环，来获得s的所有长度等于p的子串，比较每个子串和p是否由相同的若干字符构成，是的话将子串起始位加入到要返回的列表中。
    子问题：如何判断子串与p串 是由相同字符构成的？ 可以使用字典或者hashmap。
    
    但是，仔细分析，我们会发现，两层循环构成的时间复杂度为T(n)=(m)*(n-m+1)。
    当 m = (n+1)//2 时，时间复杂度最大，为T(n)=(1/4(n+1)^2),即O(n^2) 这复杂度已经很高了，所以此方法不可取。
    
2.滑动窗口法：
    仔细观察方法1的过程，我们发现，方法1每次获得下一个子串时，需要重新遍历上一次已经遍历过的部分子串（len(x)=m-1），这在无形之中增加了时间复杂度，如果我们能将这重复的遍历部分省去，可以将时间复杂度降到O(n)。
    那么如何去做到这点？我们得到新子串不一定要重新遍历，而是通过修改:
    step A: 将当前的子串的向后一位加入子串 （加入是指频次加1）
    step B: 将当前子串的起始位删去（删去是指频次减1）
    通过以上两步，就可以得到下一个子串，并且这种方法的时间复杂度为o(1),因为和p或者s的长度无关。
    这样，整个算法的时间复杂度取决于外循环，也即O(n).
"""

class Solution(object):
    def findAnagrams(self, s, p):
        """
        type s: str, type p: str, rtype: List[int]
        """
        # sliding window
        res = []
        n, m = len(s), len(p)
        if n < m: return res
        phash, shash = [0]*123, [0]*123
        for x in p:
            phash[ord(x)] += 1
        for x in s[:m]:
            shash[ord(x)] += 1
        for i in range(0, n-m+1):
            if shash == phash:
                res.append(i)
            if i + m <n: #保证不超过串s尾部
                shash[ord(s[i+m])] += 1
                shash[ord(s[i])] -= 1
        return res

总结一下：滑动窗口算法是利用一个窗口来保存当前的信息，然后获得新窗口采用的是一个增加操作和一个删减操作，常数时间复杂度，外循环为O（n）复杂度，因此总的复杂度为O（n）.如果用两层循环解决的话，内循环时间复杂度为O（m），外循环为O（n）,因此总时间复杂度为O（mn），且当m接近n的一半时，复杂度高达O（n^2）.

本次内容就到这啦~

说明
本文章所有代码及文档均以上传至github中，感谢您的rp and star.

github链接：https://github.com/LSayhi
仓库链接：https://github.com/LSayhi/Algorithms

CSDN链接：https://blog.csdn.net/LSayhi

微信公众号：AI有点可ai