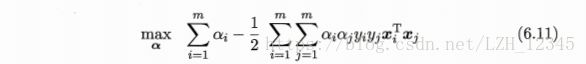《机器学习实战》第六章学习笔记(SVM)
一、支持向量机原理
1.1 间隔和支持向量
1.2 对偶问题
对式6.6,利用拉格朗日乘子法得到其对偶问题:
首先得拉格朗日函数:
最后利用式6.9消去6.8中的w和b,得对偶问题:
二、 SMO算法(Sequential Minimal Optimization)
2.1 SMO原理
SMO是一个二次规划算法,能高效的解决上述问题。其思路:
![]()
2.2 简化版SMO算法
代码实现:
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 23 19:42:07 2018
**************************SMO****************************
@author: lizihua
"""
import numpy as np
from numpy import mat,zeros,shape,multiply,nonzero,arange
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
#SMO算法中的辅助函数
#加载数据,获取数据集(X1,X2)和标签(y)
def loadDataSet(filename):
dataMat = [];labelMat = []
fr= open(filename)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
#返回一个范围在[0,m)之间的整数,且不等于j值
def selectJrand(i,m):
j=i
while(j==i):
j=int(np.random.uniform(0,m))
return j
#使得alpha的值始终在(L,H)开区间内
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
#简化版的SMO算法
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
dataMatrix = mat(dataMatIn);
labelMat = mat(classLabels).transpose()
m,n = shape(dataMatrix)
b=0;
alphas =mat(zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0 #用来记录alpha是否被优化
for i in range(m):
#f(xi)=w.T+b=(a*y).T*(X*Xi.T)+b(矩阵形式)
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*(dataMatrix[i,:].T)))+b
#误差Ei,若误差|Ei|toler
if ((labelMat[i]*Ei) < -toler and (alphas[i] < C)) or ((labelMat[i]*Ei>toler) and (alphas[i]>0)):
#选取一个等于i的j值,使得aj和ai成为一对alpha对
j = selectJrand(i,m)
#同上
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b
Ej = fXj - float(labelMat[j])
alphaIOld = alphas[i].copy()
alphaJOld = alphas[j].copy()
#保证了alpha在0~C之间,L< aj < H,最终推出 0 ai=0,aj=C或aj=0,ai=C
#ai+aj=0或2C ==>ai=0,aj=0或aj=C,ai=C
if L==H:
print("L==H")
continue
eta = 2.0 *dataMatrix[i,:]*dataMatrix[j,:].T-dataMatrix[i,:]*dataMatrix[i,:].T-dataMatrix[j,:]*dataMatrix[j,:].T
#eta>=0,则退出当前迭代过程
if eta >=0:
print("eta>0")
continue
alphas[j] -= labelMat[j]*(Ei-Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
#检查aj是否轻微改变
if abs(alphas[j]-alphaJOld)<0.00001:
print("aj轻微改变")
#若是,则退出for循环
continue
#此时,改变ai,其中ai和aj改变的大小一样,但改变的方向刚好像相反,
#从而使得所有alpha始终满足全部的ai*label(i)之和=0
alphas[i] += labelMat[j]*labelMat[i]*(alphaJOld - alphas[j])
b1 = b-Ei - labelMat[i]*(alphas[i]-alphaIOld)*dataMatrix[i,:]*dataMatrix[i,:].T-labelMat[j]*(alphas[j]-alphaJOld)*dataMatrix[j,:]*dataMatrix[j,:].T
b2 = b-Ej - labelMat[i]*(alphas[i]-alphaIOld)*dataMatrix[i,:]*dataMatrix[j,:].T-labelMat[j]*(alphas[j]-alphaJOld)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b=b1
elif (0 < alphas[j]) and (C > alphas[j]):
b=b2
else:
b=(b1+b2)/2.0
alphaPairsChanged += 1
print("iter: %d i: %d,pairs changed %d"%(iter,i,alphaPairsChanged))
if(alphaPairsChanged == 0):
iter += 1
else:
iter = 0
print("迭代次数:%d"% iter)
return b,alphas
#计算w
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#利用简化版SMO算法,绘制图像结果(包括带圈的支持向量和分割超平面)
def smoSimplePlot():
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
fr = open('testSet.txt')
for line in fr.readlines():
lineSplit = line.strip().split('\t')
xPt = float(lineSplit[0])
yPt = float(lineSplit[1])
label = int(lineSplit[2])
if (label == -1):
xcord0.append(xPt)
ycord0.append(yPt)
else:
xcord1.append(xPt)
ycord1.append(yPt)
fr.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord0,ycord0, marker='s', s=90)
ax.scatter(xcord1,ycord1, marker='o', s=50, c='red')
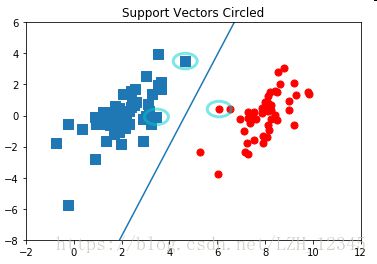
plt.title('Support Vectors Circled')
#用圈画出支持向量
circle = Circle((4.658191, 3.507396), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((3.457096, -0.082216), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((6.080573, 0.4188856), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
b = -3.83768893; w0=0.81418846; w1=-0.2725952
x = arange(-2.0, 12.0, 0.1)
#分隔超平面
y = (-w0*x - b)/w1
ax.plot(x,y)
ax.axis([-2,12,-8,6])
plt.show()
#测试
if __name__ =="__main__":
dataArr,labelArr = loadDataSet('testSet.txt')
b,alphas = smoSimple(dataArr,labelArr,0.6,0.001,40)
print("b:",b)
print("大于0的alphas值:",alphas[alphas>0])
for i in range(100):
if alphas[i]>0:
print(dataArr[i],labelArr[i])
ws = calcWs(alphas,dataArr,labelArr)
print("ws:",ws)
smoSimplePlot()
部分结果显示:
2.3 完整版SMO算法
在几百个点组成的小规模数据集上, 简化版SMO算法的运行是没有什么问题的, 但是在更大的数据集上的运行速度就会变慢。而完整版的 SMO算法在执行时存在一定的时间提升空间。与简易版SMO算法相比,alpha的更改和代数运算的优化环节一模一样,唯一的不同就是选择alpha的方式。
代码实现:
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 23 19:42:07 2018
**************************SMO****************************
@author: lizihua
"""
import numpy as np
from numpy import mat,zeros,shape,multiply,nonzero,arange
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
#加载数据,获取数据集(X1,X2)和标签(y)
def loadDataSet(filename):
dataMat = [];labelMat = []
fr= open(filename)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
#完整版的SMO算法
#定义一个数据结构,来保存所有的重要值
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2)))
#计算误差Ek
def calcEk(oS, k):
fXk =float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
#启发式算法:
#选取两变量对应样本之间的间隔最大,这样更新变量可以给目标函数值带来最大的变化
#返回Ej和j
def selectJ(i, oS, Ei):
maxK = -1; maxDeltaE = 0; Ej = 0
#输入Ei,并在缓存中设置为有效(有效意味着计算好了的)
oS.eCache[i] = [1,Ei]
#matrix.A的作用是将matrix转换为array
"""
numpy.nonzero(array)的用法
#numpy.nonzero(array)函数作用是将array中的非零元素索引以元组的形式展示
#eg:x = np.eye(3);np.nonzero(x) #result: (array([0, 1, 2]), array([0, 1, 2])),即(0,0),(1,1),(2,2)
# x[np.nonzero(x)] #result:array([ 1., 1., 1.])
#np.transpose(np.nonzero(x)) #result:array([[0, 0],[1, 1],[2, 2]])
"""
validEcacheList = nonzero(oS.eCache[:,0].A)[0] #获取非零元素的行数,而结果只有一列
if (len(validEcacheList)) > 1:
#在有效的Ek中循环,找到使得deltaE最大的j
for k in validEcacheList:
if k == i: continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
#第一次循环时,由于只有Ei是有效值,所以,需要随机选择一个alpha值,计算Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
#在alpha值改变后更新Ek
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
#完整版SMO的内循环优化代码
#选择第2个alpha,并作优化处理,若存在一对alpha值改变,则返回 1
def innerL(i, oS):
Ei = calcEk(oS, i) #计算Ei
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #利用最大步长来选择第2个alpha值
#以下过程与smoSimple()函数基本一样
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
print("L==H")
return 0
eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #alpha改变时记得更新eCache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
#完整版SMO外循环代码
def smoP(dataMatIn, classLabels, C, toler, maxIter): #full Platt SMO
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)
iter = 0
entireSet = True; alphaPairsChanged = 0
#退出循环条件:1.迭代次数超过指定的最大值 2.遍历整个集合都未对任意alpha对进行修改
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #遍历所有的值
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else: #遍历非边界值
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
print("iteration number: %d" % iter)
return oS.b,oS.alphas
#计算w
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#利用简化版SMO算法,绘制图像结果(包括带圈的支持向量和分割超平面),根据后面的得出的参数,填补下面的一些数据
def smoPPlot():
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
fr = open('testSet.txt')
for line in fr.readlines():
lineSplit = line.strip().split('\t')
xPt = float(lineSplit[0])
yPt = float(lineSplit[1])
label = int(lineSplit[2])
if (label == -1):
xcord0.append(xPt)
ycord0.append(yPt)
else:
xcord1.append(xPt)
ycord1.append(yPt)
fr.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord0,ycord0, marker='s', s=90)
ax.scatter(xcord1,ycord1, marker='o', s=50, c='red')
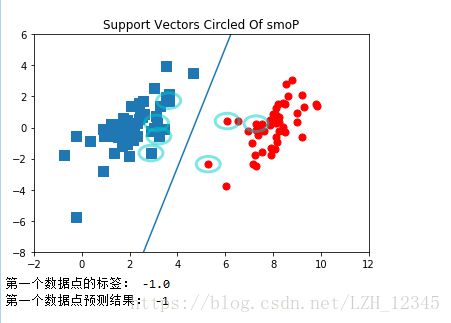
plt.title('Support Vectors Circled Of smoP')
#用圈画出支持向量
circle = Circle((3.634009, 1.730537), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((3.125951, 0.293251), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((3.223038, -0.552392), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((7.286357, 0.251077), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((2.893743, -1.643468), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((5.286862, -2.358286), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
circle = Circle((6.080573, 0.418886), 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
b = -3.5853339; w0=0.76787086; w1=-0.19996115
x = arange(-2.0, 12.0, 0.1)
#分隔超平面
y = (-w0*x - b)/w1
ax.plot(x,y)
ax.axis([-2,12,-8,6])
plt.show()
if __name__ =="__main__":
dataArr,labelArr = loadDataSet('testSet.txt')
#完整版SMO算法运行出的SVM参数
b,alphas = smoP(dataArr,labelArr,0.6,0.001,40)
print("b:",b)
for i in range(100):
if alphas[i]>0:
print(dataArr[i],labelArr[i])
ws = calcWs(alphas,dataArr,labelArr)
print("ws:",ws)
#绘制完整版SMO支持向量和超平面
smoPPlot()
#对数据进行分类
#例如,对第一个数据点进行分类
#首先,获取第一个数据点的标签,以便与预测结果比较
print("第一个数据点的标签:",labelArr[0])
#预测第一个数据点的分类结果
print("第一个数据点预测结果:",1 if (mat(dataArr[0])*mat(ws) +b)>0 else -1)
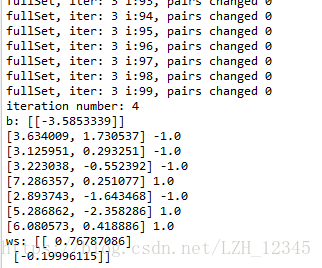
部分结果显示:
三、核函数
3.1 常用核函数
3.2 代码实现
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 25 21:44:32 2018
@author: lizihua
"""
import numpy as np
from numpy import mat,zeros,shape,multiply,nonzero,exp,sign
#加载数据
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
#返回一个范围在[0,m)之间的整数,且不等于j值
def selectJrand(i,m):
j=i
while(j==i):
j=int(np.random.uniform(0,m))
return j
#使得alpha的值始终在(L,H)开区间内
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
#创建一个数据结果,以保存相关数据
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
#计算误差Ek
def calcEk(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
#启发式算法:
#选取两变量对应样本之间的间隔最大,这样更新变量可以给目标函数值带来最大的变化
#返回Ej和j
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
#在alpha值改变后更新Ek
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
#完整版SMO的内循环优化代码
#选择第2个alpha,并作优化处理,若存在一对alpha值改变,则返回 1
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print("L==H"); return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
if eta >= 0: print("eta>=0"); return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
#完整版SMO外循环代码
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
print("iteration number: %d" % iter)
return oS.b,oS.alphas
#计算w
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#核函数
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem --That Kernel is not recognized')
return K
#k1可改变,可试试结果变化
def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet('testSetRBF.txt')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelMat[svInd];
print("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount)/m))
if __name__ =="__main__":
testRbf()
3.3部分结果显示
四、利用SVM实现手写数字识别
代码实现:(在上述RBF_SVM的基础上,添加以下代码)
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName) #load the training set
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9: hwLabels.append(-1)
else: hwLabels.append(1)
trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=('rbf', 10)):
dataArr,labelArr = loadImages('trainingDigits')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
print("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadImages('testDigits')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount)/m))
if __name__ =="__main__":
testDigits()部分结果显示: