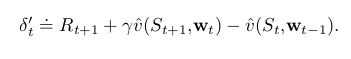强化学习系列（十二）：Eligibility Traces

一、前言

Eligibility Traces是强化学习的基本原理之一。例如TD( λ λ )算法，( λ λ )表示eligibility traces的使用情况。几乎所有TD方法，如 Q-Learning或Sarsa，都可以和eligibility traces结合起来生成更高效通用的方法。

Eligibility Traces可以用于泛化TD和MC（蒙特卡罗）方法。当用eligibility traces增强TD后，会产生一系列方法，包括两个极端的方法：MC（ λ=1 λ = 1 ）和 one step TD（ λ=0 λ = 0 ）。位于两者中间的方法比这两方法好。Eligibility Traces也提供了将MC方法用于在线连续问题的方式。

第7章中，我们介绍了一种连接TD和MC方法的n-step TD。Eligibility Traces的连接方式提供了一种更为优雅的算法机制，有很大的计算优势。该机制包含一个短期记忆向量，Eligibility Traces zt∈Rd z t ∈ R d ，对应一个长期权重向量 wt∈Rd w t ∈ R d 。基本思想是 wt w t 中参与生成estimated value的元素对应的 zt z t 中的元素波动并逐渐衰减。如果在trace衰减到0之前，TD error不为零时，则该 wt w t 中参与生成estimated value的元素会一直持续学习。trace-decay 参数 λ∈[0,1] λ ∈ [ 0 , 1 ] ，表示trace的后退速度。

与n-step方法相比：

• Eligibility Traces方法只需要存储一个trace vector，而不是n个最新的feature vectors。
• 而且学习过程是连续且时间均匀的，不会有延迟。不需要在episode结束时刻立即进行所有运算。
• 学习可以立刻影响行为，不需要n step后才延迟生效。

Eligibility Traces 表明学习算法换种方式进行运算可能会获得一定的计算优势。很多算法都比较符合自然逻辑，向前看几步，根据未来的预测调整当前的量，如MC算法根据future reward的所有量，来更新state，n-step TD根据next n rewards来更新。这种向前看的形式，称为 forward views。通常 forward views不太实用，因为更新依赖于当前不可得到的量。本章中，我们将介绍另一种类似的更新方式，有时甚至完全一样，采用eligibility trace从当前TD error 向后看最近经过的states。这种方式称为 backward views。

本章首先，从 state value和 prediction 问题说起，再将其扩展到action value和control 问题中。先讨论on-policy问题，再扩展到off-policy问题。重点讨论 linear function approximation。

二、The λ λ - return

第7章中定义了n-step return

对tabular learning而言，该式可作为 approximate SGD learning update 的update target。这个结论对n-step returns的平均值也成立，只要权重和为1，如 12Gt:t+2+12Gt:t+4 1 2 G t : t + 2 + 1 2 G t : t + 4 ，这种组合return的方式和 n-step return 一样通过减小 TD error来更新，因此可以保证算法收敛。 Averaging方式可以衍生出一系列新算法，如将 one-step 和infinite-step return平均获得 TD和MC之间的另一种算法，通过将experience-based update 和 DP update 取平均值，可以将experience-based 和model-based 方法结合。

这种将简单元素取平均的更新方式叫做 compound update。 12Gt:t+2+12Gt:t+4 1 2 G t : t + 2 + 1 2 G t : t + 4 就是一种compound update，其backup 图如下：

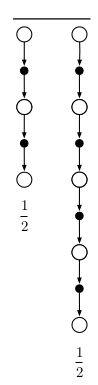
A compound update can only be done when the longest of its component
updates is complete。该更新只有在t+4时刻才能估计t时刻的值。一般会限制最长元素的长度，因为会延迟update的响应。

TD( λ λ )算法是一种特殊的averaging n-step update，包括所有n-step updates，权重系数分别为 λn−1 λ n − 1 ， λ∈[0,1] λ ∈ [ 0 , 1 ] ，由（1- λ λ ）归一化处理， λ λ -return 定义如下：

backup 图如图所示：

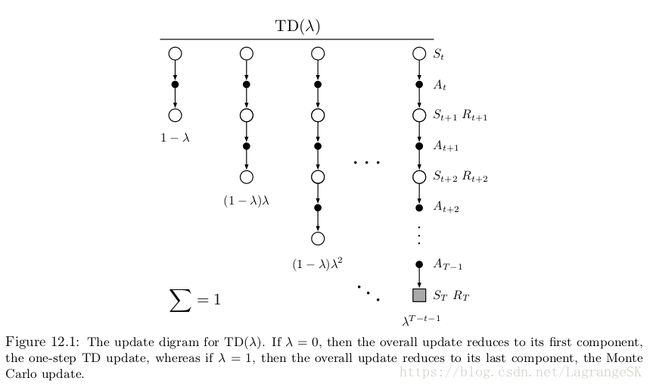
所有子n-step return的总和为 Gt G t ：

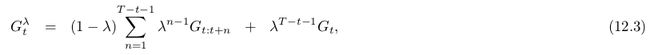
当 λ=1 λ = 1 时，为MC方法的return，当 λ=0 λ = 0 时，为one-step TD的 return。

现在定义以 λ λ -return 为update target的第一个算法——off-line λ λ -return algorithm。在episode中，权重向量不变，episode结束时，整个off-line update 序列按照 semi-gradient rule更新：

λ λ -return 使得MC和one-step TD可以平顺过渡，以19-state random walk task(第七章例子）为例，和n-step TD 结果进行比较：

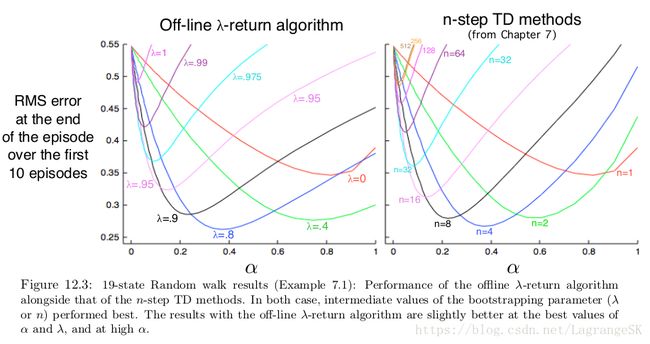
整体结果差不多，两个任务中，都是中间参数表现比较好，即n-step方法中n取中间值， λ λ -return算法中 λ λ 取中间值。

目前我们讨论的方法都叫做 forward views算法。这什么意思呢？想向我们是一个拿着望远镜的小人，在每一个state处都可以看到未来一些时刻的事情。

看到了之后，我们会更新当前state，然后我们来到了下一个state，就不需要之前的states啦！future states会被不断观测和改变。

三、TD( λ λ )

TD( λ λ ) 是强化学习中最古老且应用最广泛的算法，也是第一个阐述了forward-view 和backward-view间联系的算法（It was the first algorithm for which a formal relationship was shown between a more theoretical forward view and a more computationally congenial backward view using eligibility traces.）本节我们将介绍如何逼近上一小节提到的 off-line λ λ -return algorithm。

TD( λ λ )对off-line ( λ λ )-return算法进行了三点提升：

• 单步更新权重向量，无需等到episode结束，学习更快
• 计算在时间上均匀分布
• 不仅可用于episode问题，还适用于连续问题

本节介绍semi-gradient version of TD( λ λ ) with function approximation。在函数逼近时，eligiblility trace zt∈Rd z t ∈ R d 和权重向量 wt w t 的元素个数相同，但权重向量有长期记忆，存在时间和系统等长， zt z t 是短期记忆，存在时间小于一个episode长度。eligiblility trace存在于学习过程中，their only consequence is that they affect the weight vector, and then the weight vector determines the estimated value。

在TD( λ λ ) 中，eligiblility trace vector 在episode开始时初始化为0，每个time step 由value梯度更新，且以 γλ γ λ 衰减：

γ γ 是discount rate,eligiblility trace一直追踪那些对recent state valuation有贡献的权重向量。这里 recent 是以 γλ γ λ 界定的。回忆线性函数逼近， ∇v̂ (St,wt) ∇ v ^ ( S t , w t ) 是特征向量 xt x t ，于是eligiblility trace vector只是所有过去衰减的输入向量和。trace暗示了当reinforcing event出现时的权重向量元素的重要程度，reinforcing event只得是one-step TD errors。state-value prediction的TD error为

在TD( λ λ )中，权重更新公式为

算法伪代码如下:

TD( λ λ )是backward in time的，即每个时刻，我们由当前TD error，按照对当前eligiblility trace的贡献程度，将其分配给之前的states。可以想象我们是一个拿着话筒的小人。沿着state 流计算 TD error，然后对之前经过的state 回喊。

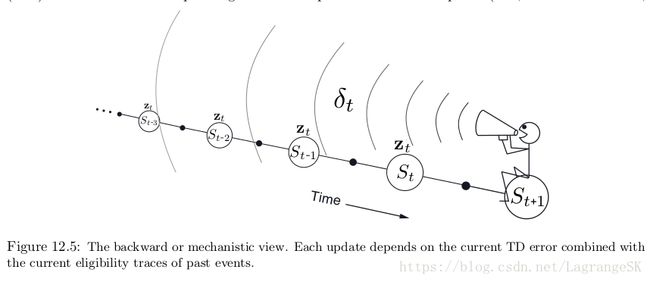
有了TD error和trace，根据式（12.7）可以进行更新，当这些过去经历的states再次出现时更新他们的state value。

为了更好的理解backward view，从 λ λ 入手。当 λ=0 λ = 0 时，式（12.5）中 t 时刻的trace恰好是 St S t 对应的value gradient，因此（12.7）中的TD( λ λ )更新变为第9章中的one-step semi-gradient TD updaet。这是第6章中的one-step TD方法被称为TD(0)的原因。在图12.5中，TD(0)只改变了当前state的TD error。当 λ<1 λ < 1 时， λ λ 越大，所涉及的之前的states越多，但越远的state变化越小，因为对应的eligiblility trace越小、表示早期的state对当前TD error 的置信度较低。

当 λ=1 λ = 1 时，早期state的置信度每步只衰减 γ γ ，刚刚好可以生成MC算法的行为。例如 记TD error 为 δt δ t ，包含一个undiscounted 的reward Rt+1 R t + 1 。从该时刻向前追溯k 个step要打 γk γ k 折，当 λ=1,γ=1 λ = 1 , γ = 1 时 eligiblility trace 不衰减，和MC方法在undiscounted episode task表现一致，当 λ=1 λ = 1 ，记作TD(1)。

TD(1)是MC方法的一种通用表达，扩展了应用范围，第5章中提到的MC方法局限于episode task，TD(1)可以用在discounted continuing task中。另外，TD(1)也可以迭代和在线学习，MC方法的一个缺点在于只能在一个episode结束时学习。

如果MC方法在episode结束前采取了一个bad action（产生了很不好的reward），那么MC继续选择这个action的趋势不会被减弱。但on-line TD(1)，从incomplet ongoing episode 中学习n-step TD ,如果有特别好或者坏的情况发生，TD(1) control menthods 可以立即学习并在同一个episode中更改行为。

仍然以19-state random walk example为例（例子7.1），来比较TD( λ λ )和 off-line λ λ -return algorithm。

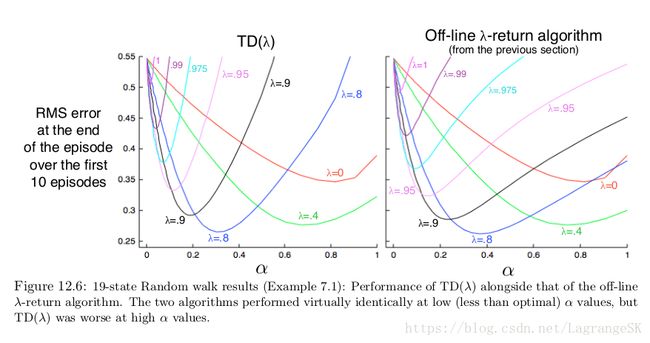
对任意 λ λ ，如果选择合适的 α α ，那么两个算法性能没有什么区别，但如果 α α 选择过大， λ λ -return algorithm只比TD( λ λ )坏一点。

当step-size 参数 α α 逐渐衰减时，在linear TD( λ λ )被证明在on-policy case中是收敛的。满足：

四、n-step Truncated λ λ -return Methods

off-line λ λ -return algorithm 是一个很重要的思想，但用处有限，因为用了一个 λ λ -return ，在episode结束前是一个未知量。在continuing case中， λ λ -return从来就是未知的，因为取决于n-step returns，n可以任意大，因此reward为遥远将来的任意值。但这种影响随着距离增大而削弱，很自然想到可以在一定步数后将序列截断。n-step returns提供了一个方法，用estimated values代替抛弃的reward。

我们定义 truncate λ λ -return如下：

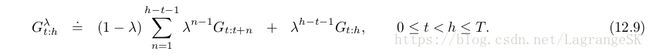
和 λ λ -return的公式对比，h和终止时刻 T的作用一致。但 λ λ -return的权重是根据 true return获得。

truncated λ λ -return 是n-step λ λ -return的一种。这类算法中，update被延迟了n步，只计算了前 n个reward，但现在用到了所有的k-step returns（ 1<=k<=1) 1 <= k <= 1 ) （n-step 算法只用了n-step return）。在state-value case中，该算法被称为 truncate TD( λ λ )，或TTD( λ λ )，backup图如下所示：

和TD( λ λ )很像，但最长的元素是n step，而不是整个episode，TTD( λ λ )的权重更新公式为：

其中：

五、Redoing Updates: The Online λ λ -return Algorithm

选择Truncated TD( λ λ )中的truncation 参数n涉及到一种平衡，n应该足够大使得该方法和 off-line λ λ -return算法接近，但也应该足够小，使得算法能够快速更新。鱼与熊掌可以兼得吗？如果以牺牲计算复杂度为代价是可以实现的。

每次得到一个新数据时，从当前episode起点处开始重新执行所有的更新过程，这个新的更新比之前的要好，因为将新数据纳入了当前计算，即用n-step truncated λ λ -return 作为update target ，总包含最后水平线（最后一项）。每次得到一个新数据时，将episode 延长一个水平线，可以获得一个更好的结果。回忆n-step truncated λ λ -return定义如下：

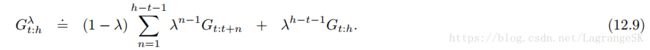
当计算复杂度不再是个问题时，来看看如何使用这个target 进行更新。一个episode开始时有一个0时刻的估计值，该估计值由上一个episode的权重 w0 w 0 计算得到。学习过程从time step 1 开始，time step 0的估计值增加一个数，可以得到 G0:1 G 0 : 1 ,包括一个 R1 R 1 和一个 v̂ (S1,w0) v ^ ( S 1 , w 0 ) ，即 Gγ0:1 G 0 : 1 γ ,用这个update target 更新 w1 w 1 ，那么再增加一个数会怎样？此时，有由 R2 R 2 和 S2 S 2 组成的新数据，和新权重 w1 w 1 ，for the first update from S0 S 0 ，可以构造一个更好的target Gγ0:2 G 0 : 2 γ ,for the second update from S1 S 1 ,可以构造更好的update target Gγ1:2 G 1 : 2 γ 。循环往复。

为了更好的理解上述思想，我们用 wht w t h 表示t时刻以h为地平线（最后一个元素结束位置）的权重向量。每个序列中的第一个权重向量 wh0 w 0 h 都从上一个episode中继承，最新的权重向量 whh w h h 表示表示该算法的权重向量端点。当 h=T h = T 时，我们得到最终的权重 wTT w T T ,用来组成下一个episode的初始权重。前三步学习过程如下:

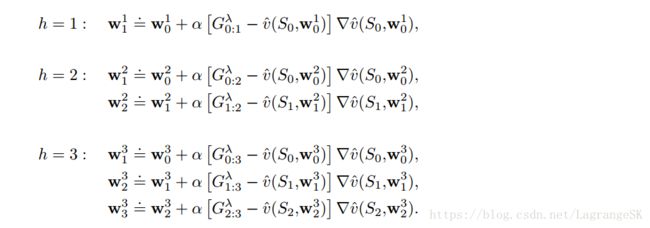
一般表达形式如下：

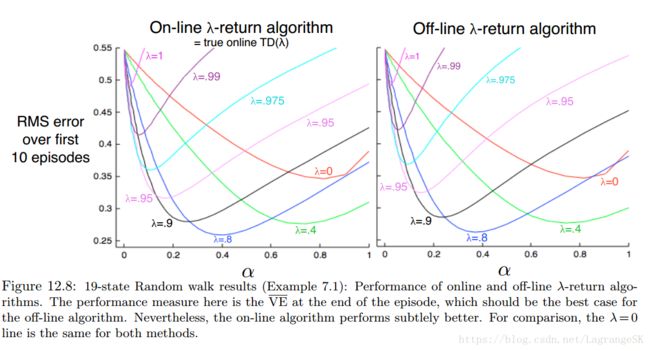
online λ λ -return algorithm是完全在线算法，在episode中，每步t 都使用t 时刻已有数据产生一个新的权重向量 wt w t ,主要缺点在于计算复杂度高，每次都要从头开始计算整个 episode，比 off- line λ λ -return方法的计算复杂度高，off-line λ λ -return方法仅在termination 处从头开始计算，在其他位置不更新。on-line方法效果比off-line好，有两点原因：

• episode 中每步更新
• episode结束时的权重系数被更新了很多次。

仍然以19-states random walk 为例，比较on-line 和off-line λ λ -return的性能，结果如下：

六、True Online TD( λ λ )

on-line λ λ -return方法是目前性能最好的TD算法，但计算复杂度太高。有没有办法将这种forward-view算法用eligibility trace转换为有效的backward-view算法呢？答案是肯定的。这就是true on-line TD( λ λ )。

true on-line TD( λ λ ) 的起源比较复杂，但方法简单，我们不讨论起源，只讨论方法。on-line λ λ -return方法所产生的权重序列如下：

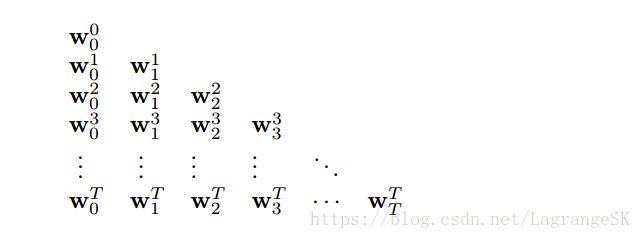
每个time step产生这个三角形的一行，但其实只需要对角线上的 wtt w t t , w00 w 0 0 是input， wTT w T T 是output， wtt w t t 将n-step return作为update target 步步更新获得。最后算法中的权重表示为 wt=wtt w t = w t t ，去掉下标。该方法需要找到一个简单有效的方法从上一个权重值来计算 wtt w t t ，如果计算出 wtt w t t ，对linear case, v̂ (s,w)=wTx(s) v ^ ( s , w ) = w T x ( s ) ,得到 true on-line TD（ λ λ ）算法：

其中， xt=x(St) x t = x ( S t ) ， δt δ t 是TD error, zt z t 定义如下：

该算法可以产生和on-line λ λ -return 算法一样的权重向量，该方法的存储要求和 TD（ λ λ ）一样，但计算提速50%，算法伪代码如下：

在true on-line TD ( λ λ )中使用的eligiblility trace称为 dutch trace以和TD( γ γ )中的区分（accumlating trace）。

七、Dutch Traces in Monte Carlo Learning

尽管eligibility trace 与TD learning有很大的历史渊源，但实际上他们并无关系。事实上，eligibility trace起源于Monte Carlo learning。第9章中，我们提到linear MC algorithm是一种forward view，可以用dutch traces将其转化为 backward view。这是本书中关于forward view 和backward view 唯一相等的转化阐述。对 true online TD( λ λ )和 on-line λ λ -return算法相等的证明提供了帮助。

The linear version of the gradient Monte Carlo prediction algorithm (page 163)的权重更新公式如下：

为了简化，假设G是在episode 结束时获得的单独reward(去掉时间下标），且undiscounted。本例中的update 被称作 least mean square(LMS) rule 。对MC而言，所有的update都取决于最终的reward /return，都要等episode 结束后才能更新。传统MC算法是off-line算法，我们并不打算从这方面缺点（也可以说是特点）去提升他。我们仍然在episode结束后才进行更新，但在episode中的每一步都进行一些计算，而不是只在episode结束处进行计算，这会使得每步的计算复杂度相同（ O(d) O ( d ) ），也避免了每步都存储feature vectors，然后在episode 结束处一次性使用的麻烦。另外，我们会介绍一个记忆向量（eligibility trace), 用来存储所有过去经过的feature vector。可以在episode结束处，快速再现一个和MC update (12.13)序列相同的全局update：

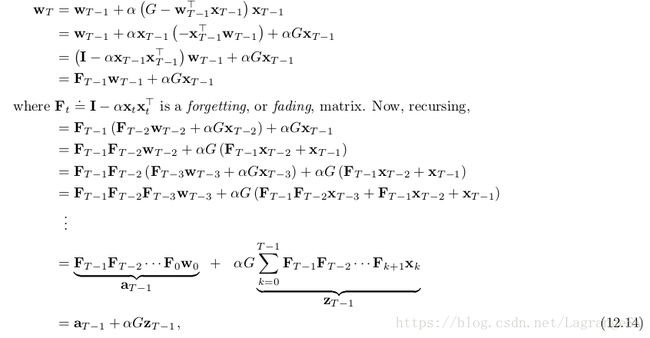
其中， aT−1 a T − 1 和 zT−1 z T − 1 是T-1时刻两个辅助记忆的向量，可以在不知道G的情况下以 O(d) O ( d ) 的复杂度迭代更新。 zt z t 向量实际上是一个dutch-style eligibility trace。初始化为 z0=x0 z 0 = x 0 ，更新公式如下：

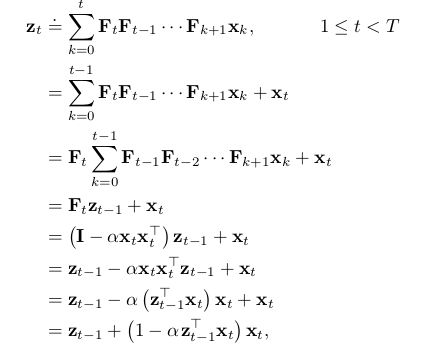
是 γλ=1 γ λ = 1 的dutch trace（式（12.11）)的特例， a a 初始化为 a0=w0 a 0 = w 0 ，更新公式如下：

在 t<T t < T 时，每步都先更新辅向量 at a t 和 zt z t ，当T时获得G,再根据公式（12.14）计算 wT w T 。和MC/LMS算法结果相同，但计算简单。这表明eligibility不是一个局限于TD learning 的方法。The need for eligibility traces seems to arise whenever one tries to learn long-term predictions in an efficient manner.

八、Sarsa( λ λ )

前面谈到了将 eligibility trace 用于state-value ，将其扩展到action-value,只需要改变一点点。此时需要学习的目标由approximate state value v̂ (s,w) v ^ ( s , w ) 变为 approximate action value q̂ (s,a,w) q ^ ( s , a , w ) ，我们需要采用第10章中提到的action-value形式的n-step return：

有了这个return，我们可以根据公式（12.9）构造action-value形式的truncated λ λ -return，那么我们可以得到action-value形式的off-line λ λ -return algorithm：

其中 Gλt=Gλt:∞ G t λ = G t : ∞ λ ，图12.9展示了forward view的backup 图，和TD（ λ λ )算法相似，只是从一个action 开始，而非从一个state开始。

用于更新action-value的TD方法——Sarsa( λ λ )是一种forward view算法，和TD（ λ λ )的更新方式一样：

其中

算法伪代码如下：

例子12.1：Traces in Gridworld
采用 eligibility trace可以提高控制算法的效率，可以超过one-step 方法甚至 n-step方法。下面以gridwaorld为例子进行说明：

左一表示一个agent在一个episode下走的路径，初始的estimated value为0，除了终点处的reward为G外，其他地方的reward都为 0 。其他图中的箭头表示算法的变化，action-value的变化方向和变化程度。one-step方法如图左二，只更新最靠近终点的action value,n_step method对前n步的action value 均等的更新，而eligibility trace方法更新从episode开始到结束的所有action value ,但随距离终点距离衰减，越远衰减越厉害。这种衰减方法通常表现最好。

前面说了action-value形式的off-line λ λ -return algorithm，下面将介绍action-value形式的online λ λ -return algorithm。在第5节中提到的online λ λ -return algorithm只需要将state value 变为action value。结合linear function approximation，可以得到 True Online Sarsa( λ λ )。算法伪代码如下：

九、Variable λ λ and γ γ

本节介绍基本TD learning 算法的最后一部分。为了用通用的形式描述算法，通常描述受到state 和action的潜在影响的参数（而不是常值参数）下的bootstrapping和discounting的程度。因此，每个time step都有一个不同的 λ λ 和 γ γ ，记作 λt λ t 和 γt γ t 。现在将 λ:SXA→[0,1] λ : S X A → [ 0 , 1 ] 表示为所有states和actions对应的整个函数 λt=λ(St,At) λ t = λ ( S t , A t ) ，同样 γ：S→[0,1] γ ： S → [ 0 , 1 ] 表示为 γt=γ(S−t) γ t = γ ( S − t ) 集合。

首先来看 γ γ ,(termination function),这是一个可以改变return的形式的重要参数。现在定义return如下：

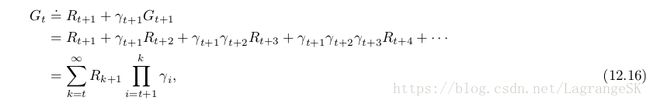
为了保证求和是有限的，我们要求对所有t有 Π∞k=tγk=0 Π k = t ∞ γ k = 0 。这种定义的方便之处在于允许按episode执行，有起点和终点。终止状态的 γ=0 γ = 0 ，然后转移到开始状态。取 γ(.) γ ( . ) 为常值函数可以得到episode setting的特例。以state为自变量的termination γ（St) γ （ S t ) 包含另一种prediction case——soft termination ，我们试图找到一个量使得prediction完整性更高，但不改变马尔科夫过程。Discounted returns 就是这样一个量，state dependent termination γ（St) γ （ S t ) 是episode和discounted-continuing cases的深层特性（undiscounted-continuing case需要一些特殊处理）。

接下来将介绍对bootstrapping的泛化。和discounting一样，但求解方法需要进行一些调整。因为涉及state和action两个变量。new state-based γ γ -return可以写作：

这里，我们对 λ λ 加上了“s” 的下标，表示这是根据states value 得到的值，对应的 action value 的 λ λ 有一个“a”的下标。action-based λ λ -return is either the Sarsa from

or the Expected Sarsa form

其中：

十、off-policy Eligibility Traces with Control Variates

最后一步是合并importance sampling。和n-step 方法不同，对 full non_truncated λ λ -return算法而言，没法将importance sample用于target return之外。Instead, we move directly to the bootstrapping generalization of per-decision importance sampling with control variates (Section 7.4).In the state case, our final definition of theλ-return generalizes (12.17), after the model of (7.10), to

其中 ρt=π(At|St)b(At,St ρ t = π ( A t | S t ) b ( A t , S t ，和之前提到的returns一样，该return的truncateed 形式可以由state-based TD error函数逼近得到：

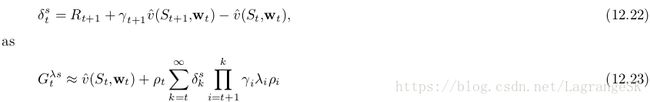
（12.23）所表示的 λ λ -return很容易用于forward-view update

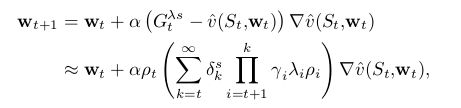
这看起来和eligibility-based TD update很像，the product is like an eligibility trace and it is multiplied by TD errors.但这只是forward view的一步，我们需要探究的是整个forward view过程和整个backward view过程的近似相等关系。整个forward-view update之和如下：

当上式的第二个求和项可以被写作eligibility trace，且可以迭代更新时，变为backward-view TD update。trace在k时刻的表达式可以由k-1时刻求得：

用t取代k,得：

This eligibility trace, together with the usual semi-gradient parameter-update rule for TD(λ) (12.7), forms a general TD(λ) algorithm that can be applied to either on-policy or off-policy data. 在on-policy中，该算法就是TD(λ) ，因为 ρt ρ t 总是1，式（12.24）变成普通累加（12.5）。在off-policy中，该算法性能ok,但semi-gradient 方法不太稳定，接下来几节我们考虑一些增强稳定性的方式。

action-value 的off-policy eligibility traces与state value类似，可以从（12.18）或（12.19）开始构建一个 action-based λ-return。我们根据（7.11）将（12.19）扩展到off-policy中，得到return：

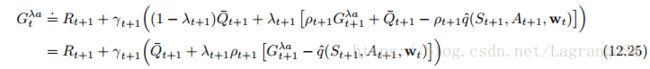
其中 Q⎯⎯⎯⎯t+1 Q ¯ t + 1 由（12.20）给出，再次用TD error之和逼近 λ-return：

此处采用 expectation form of the action-based TD error：

和state value 类似，可以根据（12.26）写出一个forward-view update,进行上述转换，最终得到the eligibility trace for action values：

This eligibility trace, together with the usual semi-gradient parameter-update rule (12.7), forms a general Sarsa(λ) algorithm that can be applied to either on-policy or off-policy data.在on-policy case中（ with constant λ and γ），该算法是第8节中讲到的 Sarsa(λ) algorithm。在off-policy case中，该算法不稳定，除非和之后章节中的方法结合。

当 λ=1 λ = 1 时，这些算法和对应的MC算法关系密切。One might expect that an exact equivalence would hold for episodic problems and off-line updating, but in fact the relationship is subtler and slightly weaker than that.

如果 λ < 1, then all these off-policy algorithms involve bootstrapping and the deadly triad applies (Section 11.3，死亡三要素：函数逼近，bootstrapping和off-policy)。第11章中讲到off-policy方法的两大挑战，不断变化的updata target和变化的update distribution。在第12节将介绍off-policy learning with eligibility traces的update distribution 挑战。

十一、Watkins’s Q(λ) to Tree-Backup(λ)

近些年来提出了很多在Q-learning上进行eligibility traces扩展的方法。最早是Watkins’s Q(λ)，which decays its eligibility traces in the usual way as long as a greedy action was taken, then cuts the traces to zero after the first non-greedy action. 该方法的backup图如下：

在第6章中，我们介绍了 Expected Sarsa 的off-policy方法（Q-learning为该方法的特例），上一节我们介绍了结合 off-policy eligibility traces的Expected Sarsa。第7章中，从n-step Tree Backup中区分了n-step Expected Sarsa,n-step Tree Backup并未使用 importance sampling。 接下来介绍eligibility trace version of Tree Backup，我们称其为Tree-Backup(λ)或TB(λ)。TB(λ)的Backup图如下：

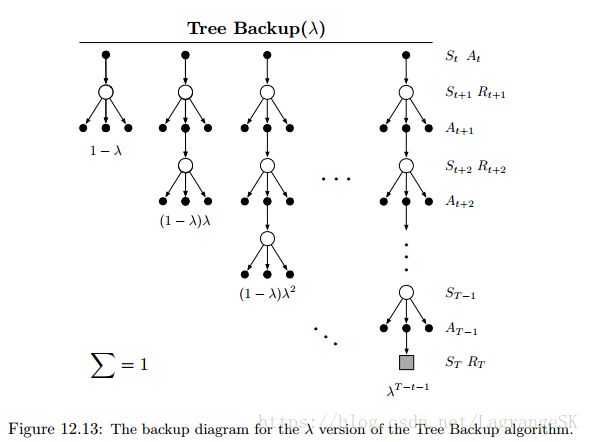
start with a recursive form (12.19) for the λ-return using action values, and then expand the bootstrapping case of the target after the model of (7.14):

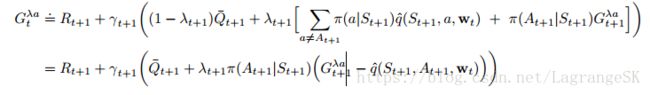
用（12.27）的TD error sum逼近 ：

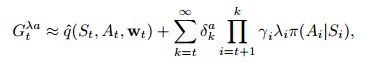
和上一节一样的步骤，得到eligibility trace update：

加上参数更新公式（12.7）构成了TB(λ) algorithm。和所有semigradient algorithms一样，TB(λ) algorithm对off-policy data和函数逼近，不能保证稳定。都需要和下一小节的方法结合起来。

十二、Stable Off-policy Methods with Traces

前几小节提到很多eligibility trace方法，都可以在off-policy training中获得稳定解，这里我们介绍本书中包括泛化bootstrapping 和discounting functions的四个最重要的标准表达。这些都基于在第11.8节提到的 Gradient-TD或11.9提到的Emphatic-TD思想。所有算法都基于Linear function approximation 假设。

---

GTD（ λ λ )——eligibility trace 算法和 TDC的结合
要学习的参数：从off-policy data中获得的 v̂ (s,w)=wTtx(s)≈vπ(s) v ^ ( s , w ) = w t T x ( s ) ≈ v π ( s ) 中的权重向量 w w

更新公式：

---

GQ( λ λ )——Gradient-TD algorithm for action value 和 eligibility trace的结合
要学习的参数：从off-policy data中获得的 q̂ (s,a,w)=wTtx(s,a)≈qπ(s,a) q ^ ( s , a , w ) = w t T x ( s , a ) ≈ q π ( s , a ) 中的权重向量 w w

更新公式：

zt z t 由（12.28）定义。其余都和GTD（ λ λ )中一样，包括 vt v t 。

---

HTD（ λ λ )——GTD( λ λ )和TD( λ λ )的中间产物,一种state-value算法
要学习的参数：从off-policy data中获得的 v̂ (s,w)=wTtx(s)≈vπ(s) v ^ ( s , w ) = w t T x ( s ) ≈ v π ( s ) 中的权重向量 w w

特点：是TD( λ λ )对off-policy learning的一次严格泛化，这意味着当behavior policy和target policy相同时，该方法完全等同于TD( λ λ )。对GTD( λ λ )而言并非如此。因为TD( λ λ )的收敛速度通常比GTD( λ λ )快，且TD( λ λ )只需要一个step size。

更新方式：

此处 β β 是second step-size 参数，当on-policy（ b=π b = π ) 时忽略不计。因为有第二个权重向量 vt v t ，所以HTD（ λ λ )有第二个eligibility trace zbt z t b ，用传统eligibility trace的更新方式更新，当 ρ=1 ρ = 1 时和 zt z t 相等，这使得 wt w t 的第二项为0 ，算法变为 TD( λ λ )

---

Emphatic TD( λ λ )——11.9节中的one-step Emphatic-TD算法结合eligibility traces
特点：该算法以高方差和慢收敛速度为代价，保证了无论采用任何程度的bootstrapping在off-policy中的收敛性。

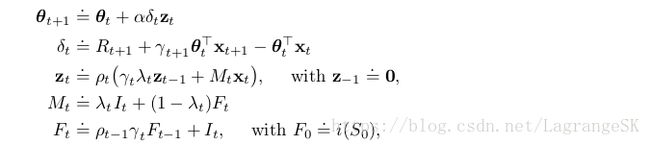
其中 Mt>0 M t > 0 表示emphasis， Ft>0 F t > 0 表示 followon trace, It>0 I t > 0 表示interest。注意 Mt M t 像 δt δ t 一样，不是一个真正的额外记忆变量，可以用于取代eligibility trace公式中的 δt δ t 。

---

十三、Implementation Issues

eligibility trace方法比one-step方法复杂。一般应用起来需要每一步都用every state( or state-action pair)来更新value estimate 和 eligibility trace。This would not be a problem for implementations on single-instruction, multiple-data, parallel computers or in plausible neural implementations, but it is a problem for implementations on conventional serial computers。但对特殊的 λ λ 和 γ γ 而言，其实大部分 state对应的eligibility trace都几乎为0 ，只有那些最近经历过的state的trace大于0，在实际应用中，只有少数state需要被更新。

对传统计算机而言，实际用eligibility trace方法时只更新少数trace不为0的state。（这个小技巧通常取决于 λ 和 γ的值 ）. Note that the tabular case is in some sense the worst case for the computational complexity of eligibility traces. When function approximation is used, the computational advantages of not using traces generally decrease. For example, if artificial neural networks and backpropagation are used, then eligibility traces generally cause only a doubling of the required memory and computation per step. Truncated λ-return methods (Section 12.3) can be computationally efficient on conventional computers though they always require some additional memory.

十四、总结

本章介绍了介于TD和MC之间的eligibility trace方法，之前介绍过的n-step TD也是一种介于TD和MC之间的方法，但eligibility trace方法是一种更优雅，学习更快，有很多变体。本章对变化的bootstrapping 和 discounting,从on-policy和off-policy对eligibility trace方法进行阐述。一方面eligibility trace方法的优雅体现在是一种true online 方法，which exactly reproduce the behavior of expensive ideal methods while retaining the computational congeniality of conventional TD methods.另一方面，揭示了forward view向backward view 的转化。将这种思想用于MC方法也完全合适。