【数据处理】奇异值分解(SVD) 数据降噪的python实现
【数据处理】奇异值分解(SVD) 数据降噪的python实现
- 一、特征值分解
- 二、奇异值分解
- 三、python实现
- 参考资料
一、特征值分解
(参考资料【1】)对称矩阵不同的特征值对应的特征向量两两正交,假设存在一个 m ∗ m m*m m∗m的满秩对称矩阵 A A A,其具有 m m m个不同的特征值分别为: λ i , i = 1 , ⋯ , m {\lambda _i},i = 1, \cdots ,m λi,i=1,⋯,m,每个特征值对应的特征向量为: x i , i = 1 , ⋯ , m {x_i},i = 1, \cdots ,m xi,i=1,⋯,m。存在如下关系:
A x i = λ i x i A{x_i} = {\lambda _i}{x_i} Axi=λixi
进而存在:
A U = U Λ AU = U\Lambda AU=UΛ
其中: U = [ x 1 , x 2 , ⋯ , x m ] U = \left[ {{x_1},{x_2}, \cdots ,{x_m}} \right] U=[x1,x2,⋯,xm], Λ = [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ m ] \Lambda = \left[ {\begin{matrix} {{\lambda _1}}& \cdots &0\\ \vdots & \ddots & \vdots \\ 0& \cdots &{{\lambda _m}} \end{matrix}} \right] Λ=⎣⎢⎡λ1⋮0⋯⋱⋯0⋮λm⎦⎥⎤。
由于对称矩阵的特征向量两两正交,所以 U U U为正交阵,正交阵的逆矩阵等于其转置,因此 A A A的特征值分解为:
A = U Λ U − 1 = U Λ U T A = U\Lambda {U^{ - 1}} = U\Lambda {U^T} A=UΛU−1=UΛUT
特征值表示原矩阵在其对应的特征向量方向上包含的信息量,特征值越大,说明其对应的特征向量在构成原矩阵的过程中承担的作用越大。
二、奇异值分解
任意 m ∗ n m*n m∗n的矩阵 A A A可以分解为如下形式(具体参考资料【1,2】):
A = U Σ V T A = U\Sigma {V^T} A=UΣVT
其中 U ( m ∗ r ) U(m*r) U(m∗r)为左奇异矩阵, V ( n ∗ r ) V(n*r) V(n∗r)为右奇异矩阵, Σ \Sigma Σ为对角矩阵,对角线上是矩阵 A A A的奇异值从大到小排列, r r r为矩阵 A A A的秩数。
Σ = [ σ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ σ r ] = [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ r ] \Sigma = \left[ {\begin{matrix} {{\sigma _1}}& \cdots &0\\ \vdots & \ddots & \vdots \\ 0& \cdots &{{\sigma _r}} \end{matrix}} \right]=\left[ {\begin{matrix} {\sqrt {{\lambda _1}} }& \cdots &0\\ \vdots & \ddots & \vdots \\ 0& \cdots &{\sqrt {{\lambda _r}} } \end{matrix}} \right] Σ=⎣⎢⎡σ1⋮0⋯⋱⋯0⋮σr⎦⎥⎤=⎣⎢⎡λ1⋮0⋯⋱⋯0⋮λr⎦⎥⎤
所以奇异值也可以表示原矩阵在其对应的特征向量方向上包含的信息量,奇异值越大,说明其对应的特征向量在构成原矩阵的过程中承担的作用越大。
如果前 k ( k < r ) k(k<r) k(k<r)个奇异值数值较大,说明前 k k k个奇异值对应的信息是原矩阵的主成分,可以重构降噪后的矩阵 A ~ \tilde A A~为:
A ~ = U m × k Σ k × k V n × r T \tilde A = {U_{m \times k}}{\Sigma _{k \times k}}V_{n \times r}^T A~=Um×kΣk×kVn×rT
三、python实现
本博文的数据对象为函数 y = 10 sin ( t ) + 5 sin ( 2 t ) + 2 r a n d ( ) y = 10\sin (t) + 5\sin (2t) + 2rand() y=10sin(t)+5sin(2t)+2rand(),并采用奇异值分解的方法确定保留下来的阶数(参考资料【3】),然后重构去燥后的信号。因为奇异值分解的处理对象为矩阵,首先需要将原始的一维数组转化为二维矩阵,重构后的矩阵在按照相反的过程转化为一维数组。
import numpy as np
import random
import matplotlib.pyplot as plt
## 1.待处理信号(400个采样点)
t = np.arange(0,40,0.1)
r = [2*random.random() for i in range(400)]
x = 10*np.sin(1*t)+5*np.sin(2*t)
xr = x+r
## 2.一维数组转换为二维矩阵
x2list = []
for i in range(20):
x2list.append(xr[i*20:i*20+20])
x2array = np.array(x2list)
## 3.奇异值分解
U,S,V = np.linalg.svd(x2array)
S_list = list(S)
## 奇异值求和
S_sum = sum(S)
##奇异值序列归一化
S_normalization_list = [x/S_sum for x in S_list]
## 4.画图
X = []
for i in range(len(S_normalization_list)):
X.append(i+1)
fig1 = plt.figure().add_subplot(111)
fig1.plot(X,S_normalization_list)
fig1.set_xticks(X)
fig1.set_xlabel('Rank',size = 15)
fig1.set_ylabel('Normalize singular values',size = 15)
plt.show()
## 5.数据重构
K = 1 ## 保留的奇异值阶数
for i in range(len(S_list) - K):
S_list[i+K] = 0.0
S_new = np.mat(np.diag(S_list))
reduceNoiseMat = np.array(U * S_new * V)
reduceNoiseList = []
for i in range(len(x2array)):
for j in range(len(x2array)):
reduceNoiseList.append(reduceNoiseMat[i][j])
## 6.去燥效果展示
fig2 = plt.figure().add_subplot(111)
fig2.plot(t,list(xr),'b',label = 'Original data')
fig2.plot(t,reduceNoiseList,'r-',label = 'Processed data')
fig2.legend()
fig2.set_title('Rank is 1')
fig2.set_xlabel('Sampling point',size = 15)
fig2.set_ylabel('Value of data',size = 15)
plt.show()
本博文采用实例中归一化的奇异值随阶数的变化趋势如下图:
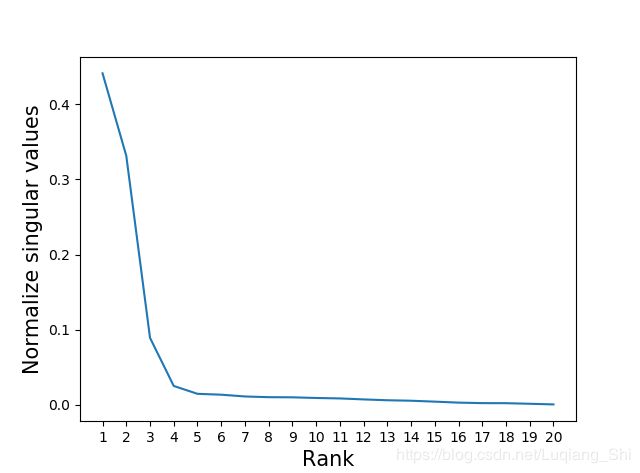
由上图可知,当阶数大于3时,对应的归一化奇异值都很小,这些奇异值对应的的特征向量包含的信息为噪声,所以我们将保留的奇异值阶数设定为3。则原始数据和去燥后的数据如下图所示:

如上图所示,原始数据的噪音被过滤。
参考资料
1、https://blog.csdn.net/u013108511/article/details/79016939
2、Kalman D . A Singularly Valuable Decomposition: The SVD of a Matrix[J]. College Mathematics Journal, 1996, 27(1):2-23.
3、练继建, 李火坤, 张建伟. 基于奇异熵定阶降噪的水工结构振动模态ERA识别方法[J]. 中国科学:, 2008(9):1398-1413.