【机器学习】广义回归神经网络（GRNN）的python实现

一、广义回归神经网络原理

1.1、GRNN与PNN的关系

广义回归神经网络（Generalized Regression Neural Network）的网络结构类似于RBF神经网络。与概率神经网络（PNN）相同，GRNN也是一个前向传播的网络，不需要反向传播求模型参数；不同的是GRNN用于求解回归问题，而PNN用于求解分类问题。关于GRNN的数学原理可以参考资料【1】。

2.2、GRNN的网络结构

如下图所示，GRNN与PNN一样也是一个四层的网络结构。

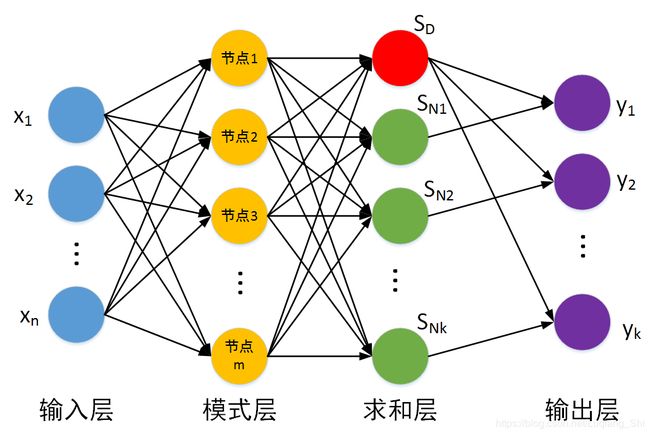
对于回归问题训练数据集包括样本特征集与标签集，假设样本特征集为：$\left\{tr{x}_1,tr{x}_2,\cdots ,tr{x}_m\right\}$，每一个样本的维度为$n$，即 $tr{x}_i=[x_1,x_2,\cdots ,x_n]$。标签集为：$\left\{tr{y}_1,tr{y}_2,\cdots ,tr{y}_m\right\}$，每一个标签的维度为$k$，即 $tr{y}_i=[y_1,y_2,\cdots ,y_k]$。

输入层：输入测试样本，节点个数等于样本的特征维度。

模式层：（与PNN的模式层相同）计算测试样本与训练样本中的每一个样本的Gauss函数的取值，节点个数等于训练样本的个数。
第$i$个测试样本$te{x}_i$与第$j$个训练样本$tr{x}_j$之间的Gauss函数取值（对于测试样本$x$，从第$j$个模式层节点输出的数值）为：

$Gauss(te{x}_i-tr{x}_j)=e^{-\frac{\Vert te{x}_i-tr{x}_j\Vert }{2{\delta }^2}}$

其中$\delta$是模型的超参数（机器学习模型中，超参数是在开始学习过程之前设置值的参数），需要提前设定，也可以通过寻优算法（GA，QGA，PSO，QPSO等）获得。

求和层：节点个数等于输出样本维度加1（$k+1$），求和层的输出分为两部分，第一个节点输出为模式层输出的算术和，其余$k$个节点的输出为模式层输出的加权和。

假设对于测试样本$tex$，模式层的输出为$\left\{g_1,g_2,\cdots ,g_m\right\}$。
求和层第一个节点的输出为：

$S_D=\sum _{i=1}^m{g}_i$

其余$k$个节点的输出为：

$S_{Nj}=\sum _{i=1}^m{y}_{ij}{g}_i,j=1,2,\cdots ,k$

其中加权系数$y_{ij}$为第$j$个模式层节点对应的训练样本的标签的第$j$个元素。
输出层：输出层节点个数等于标签向量的维度，每个节点的输出等于对应的求和层输出与求和层第一个节点输出相除。

二、广义回归神经网络的优点与不足

2.1、优点

收敛快：没有模型参数需要训练，收敛速度快。
非线性逼近：以径向基网络为基础，具有良好的非线性逼近性能。

2.2、不足

计算复杂度高：每个测试样本要与全部的训练样本进行计算。
空间复杂度高：因为没有模型参数，对于测试样本全部的训练样本都要参与计算，因此需要存储全部的训练样本。

三、GRNN的python实现

完整python代码与样本地址：https://github.com/shiluqiang/GRNN_python
本博文采用数据集为sine函数的数据集，将前190组数据作为训练集，后10组数据作为测试集。数据集中特征维度为1，标签维度也为1，因此GRNN的网络结构应该是（1：190：2：1）。
首先，计算模式层的输出。

def distance(X,Y):
    '''计算两个样本之间的距离
    '''
    return np.sqrt(np.sum(np.square(X-Y),axis = 1))

def distance_mat(trainX,testX):
    '''计算待测试样本与所有训练样本的欧式距离
    input:trainX(mat):训练样本
          testX(mat):测试样本
    output:Euclidean_D(mat):测试样本与训练样本的距离矩阵
    '''
    m,n = np.shape(trainX)
    p = np.shape(testX)[0]
    Euclidean_D = np.mat(np.zeros((p,m)))
    for i in range(p):
        for j in range(m):
            Euclidean_D[i,j] = distance(testX[i,:],trainX[j,:])[0,0]
    return Euclidean_D

def Gauss(Euclidean_D,sigma):
    '''测试样本与训练样本的距离矩阵对应的Gauss矩阵
    input:Euclidean_D(mat):测试样本与训练样本的距离矩阵
          sigma(float):Gauss函数的标准差
    output:Gauss(mat):Gauss矩阵
    '''
    m,n = np.shape(Euclidean_D)
    Gauss = np.mat(np.zeros((m,n)))
    for i in range(m):
        for j in range(n):
            Gauss[i,j] = math.exp(- Euclidean_D[i,j] / (2 * (sigma ** 2)))
    return Gauss

然后，计算求和层输出。

def sum_layer(Gauss,trY):
    '''求和层矩阵，列数等于输出向量维度+1,其中0列为每个测试样本Gauss数值之和
    '''
    m,l = np.shape(Gauss)
    n = np.shape(trY)[1]
    sum_mat = np.mat(np.zeros((m,n+1)))
    ## 对所有模式层神经元输出进行算术求和
    for i in range(m):
        sum_mat[i,0] = np.sum(Gauss[i,:],axis = 1) ##sum_mat的第0列为每个测试样本Gauss数值之和
    ## 对所有模式层神经元进行加权求和
    for i in range(m):             
        for j in range(n):
            total = 0.0
            for s in range(l):
                total += Gauss[i,s] * trY[s,j]
            sum_mat[i,j+1] = total           ##sum_mat的后面的列为每个测试样本Gauss加权之和            
    return sum_mat

最后，计算输出层的输出。

def output_layer(sum_mat):
    '''输出层输出
    input:sum_mat(mat):求和层输出矩阵
    output:output_mat(mat):输出层输出矩阵
    '''
    m,n = np.shape(sum_mat)
    output_mat = np.mat(np.zeros((m,n-1)))
    for i in range(n-1):
        output_mat[:,i] = sum_mat[:,i+1] / sum_mat[:,0]
    return output_mat

结果展示：

测试样本标签	回归结果
0.624676	0.557845
0.816921	0.881194
1.04449	0.916176
-0.30906	-0.293338
0.267336	0.126166
1.01882	0.815953
0.409871	0.296891
0.920009	0.912512
-0.112378	-0.0923096
0.768894	0.86055

参考资料

1、https://blog.csdn.net/guoyunlei/article/details/76101899?locationNum=4&fps=1