Transformer-XL解读（论文 + PyTorch源码）

前言

目前在NLP领域中，处理语言建模问题有两种最先进的架构：RNN和Transformer。RNN按照序列顺序逐个学习输入的单词或字符之间的关系，而Transformer则接收一整段序列，然后使用self-attention机制来学习它们之间的依赖关系。这两种架构目前来看都取得了令人瞩目的成就，但它们都局限在捕捉长期依赖性上。

为了解决这一问题，CMU联合Google Brain在2019年1月推出的一篇新论文《Transformer-XL：Attentive Language Models beyond a Fixed-Length Context》同时结合了RNN序列建模和Transformer自注意力机制的优点，在输入数据的每个段上使用Transformer的注意力模块，并使用循环机制来学习连续段之间的依赖关系。Transformer-XL在多种语言建模数据集（如单词级别的enwik8和字符级别的text8）上实现了目前的SoTA效果，且该模型在推理阶段速度更快，比之前最先进的利用Transformer进行语言建模的方法快300～1800倍。 同时，该论文也放出了其配套源码（包括TensorFlow和PyTorch的）、预训练模型及在各个数据集上训练的超参数，可以说是非常良心了～造福我等伸手党！

本文将主要针对模型原理及其PyTorch实现进行逐一对照解读，因笔者能力有限，如有不详尽之处，可移步文末的传送门进行详细阅读，并欢迎指出～

一. 回顾Transformer

在NLP领域中，一种对语言建模的最常用模型就是RNN，它可以捕捉单词之间的依赖关系。但因为梯度消失和爆炸的问题，RNN变得非常难以训练，LSTM单元和梯度裁剪方法的提出也不足以解决此类问题。同时RNN网络的计算速度往往很慢，其学习长期依赖的能力也较为有限（论文中提到，LSTM语言模型平均只能建模200个上下文词语）。

2017年6月，Google Brain在论文《Attention Is All You Need》中提出的Transformer架构，完全摒弃了RNN的循环机制，采用一种self-attention的方式进行全局处理。其接收一整段序列，并使用三个可训练的权重矩阵——Query、Key和Value来一次性学习输入序列中各个部分之间的依赖关系。Transformer网络由多个层组成，每个层都由多头注意力机制和前馈网络构成。由于在全局进行注意力机制的计算，忽略了序列中最重要的位置信息。Transformer为输入添加了位置编码（Positional Encoding），使用正弦函数完成，为每个部分的位置生成位置向量，不需要学习，用于帮助网络学习其位置信息。其示意如下图所示：

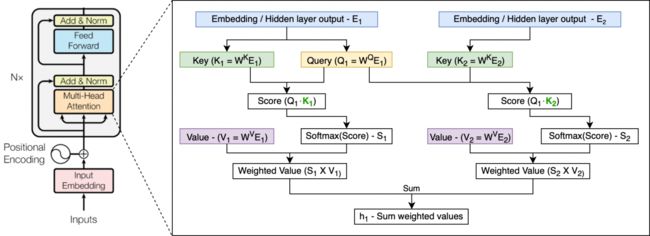
有关Transformer的更深入讨论，可参考笔者之前的博客：

Transformer（论文 + PyTorch源码解读）

二. vanilla Transformer

为何要提这个模型？因为Transformer-XL是基于这个模型进行的改进。

Al-Rfou等人基于Transformer提出了一种训练语言模型的方法（ https://arxiv.org/abs/1808.04444 ），来根据之前的字符预测片段中的下一个字符。例如，它使用$x_1,x_2,...,x_{n-1}$预测字符$x_n$，而在$x_n$之后的序列则被mask掉。论文中使用64层模型，并仅限于处理 512个字符这种相对较短的输入，因此它将输入分成段，并分别从每个段中进行学习，如下图所示。 在测试阶段如需处理较长的输入，该模型会在每一步中将输入向右移动一个字符，以此实现对单个字符的预测。

该模型在常用的数据集如enwik8和text8上的表现比RNN模型要好，但它仍有以下两个缺点：

a. 上下文长度受限：字符之间的最大依赖距离受输入长度的限制，模型看不到出现在几个句子之前的单词。
b. 上下文碎片：对于长度超过512个字符的文本，都是从头开始单独训练的。段与段之间没有上下文依赖性，会让训练效率低下，也会影响模型的性能。
c. 推理速度慢：在测试阶段，每次预测下一个单词，都需要重新构建一遍上下文，并从头开始计算，这样的计算速度非常慢。

三. Transformer-XL

Transformer-XL架构在vanilla Transformer的基础上引入了两点创新：循环机制（Recurrence Mechanism）和相对位置编码（Relative Positional Encoding），以克服vanilla Transformer的缺点。与vanilla Transformer相比，Transformer-XL的另一个优势是它可以被用于单词级和字符级的语言建模。

1. 引入循环机制

与vanilla Transformer的基本思路一样，Transformer-XL仍然是使用分段的方式进行建模，但其与vanilla Transformer的本质不同是在于引入了段与段之间的循环机制，使得当前段在建模的时候能够利用之前段的信息来实现长期依赖性。如下图所示：

在训练阶段，处理后面的段时，每个隐藏层都会接收两个输入：

1. 该段的前面隐藏层的输出，与vanilla Transformer相同（上图的灰色线）。
2. 前面段的隐藏层的输出（上图的绿色线），可以使模型创建长期依赖关系。

这两个输入会被拼接，然后用于计算当前段的Key和Value矩阵。对于某个段的某一层的具体计算公式如下：

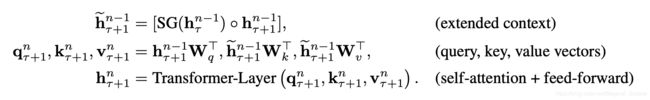
其中，$\tau$表示第几段，$n$表示第几层，$h$表示隐层的输出。$SG(\cdot )$表示停止计算梯度，$[h_u\circ h_v]$表示在长度维度上的两个隐层的拼接，$W_{.}$是模型参数。乍一看与Transformer中的计算公式很像，唯一关键的不同就在于Key和Value矩阵的计算上，即$k_{\tau +1}^n$和$v_{\tau +1}^n$，它们基于的是扩展后的上下文隐层状态${\tilde{h}}_{\tau +1}^{n-1}$进行计算，$h_{\tau }^{n-1}$是之前段的缓存。

原则上只要GPU内存允许，该方法可以利用前面更多段的信息，测试阶段也可以获得更长的依赖。

在测试阶段，与vanilla Transformer相比，其速度也会更快。在vanilla Transformer中，一次只能前进一个step，并且需要重新构建段，并全部从头开始计算；而在Transformer-XL中，每次可以前进一整个段，并利用之前段的数据来预测当前段的输出。

2. 相对位置编码

在Transformer中，一个重要的地方在于其考虑了序列的位置信息。在分段的情况下，如果仅仅对于每个段仍直接使用Transformer中的位置编码，即每个不同段在同一个位置上的表示使用相同的位置编码，就会出现问题。比如，第$i-2$段和第$i-1$段的第一个位置将具有相同的位置编码，但它们对于第$i$段的建模重要性显然并不相同（例如第$i-2$段中的第一个位置重要性可能要低一些）。因此，需要对这种位置进行区分。

论文对于这个问题，提出了一种新的位置编码的方式，即会根据词之间的相对距离而非像Transformer中的绝对位置进行编码。在Transformer中，第一层的计算查询$q_i^T$和键$k_j$之间的attention分数的方式为：

其中，$E_{x_i}$是词$i$的embedding，$E_{x_j}$是词$j$的embedding，$U_i$和$U_j$是位置向量，这个式子实际上是$(W_q(E_{x_i}+U_i){)}^T\cdot (W_k(E_{x_j}+U_j))$的展开，就是Transformer中的标准格式。

在Transformer-XL中，对上述的attention计算方式进行了变换，转为相对位置的计算，而且不仅仅在第一层这么计算，在每一层都是这样计算。

对比来看，主要有三点变化：

1. 在(b)和(d)这两项中，将所有绝对位置向量$U_j$都转为相对位置向量$R_{i-j}$，与Transformer一样，这是一个固定的编码向量，不需要学习。
2. 在(c)这一项中，将查询的$U_i^T{W}_q^T$向量转为一个需要学习的参数向量$u$，因为在考虑相对位置的时候，不需要查询的绝对位置$i$，因此对于任意的$i$，都可以采用同样的向量。同理，在(d)这一项中，也将查询的$U_i^T{W}_q^T$向量转为另一个需要学习的参数向量$v$。
3. 将键的权重变换矩阵$W_k$转为$W_{k,E}$和$W_{k,R}$，分别作为content-based key vectors和location-based key vectors。

从另一个角度来解读这个公式的话，可以将attention的计算分为如下四个部分：

a. 基于内容的“寻址”，即没有添加原始位置编码的原始分数。
b. 基于内容的位置偏置，即相对于当前内容的位置偏差。
c. 全局的内容偏置，用于衡量key的重要性。
d. 全局的位置偏置，根据query和key之间的距离调整重要性。

3. 整体计算公式

结合上面两个创新点，将Transformer-XL模型的整体计算公式整理如下，这里考虑一个N层的只有一个注意力头的模型：

其中，$\tau$代表第几段，$n$代表第几层，$h_{\tau }^0:=E_{s_{\tau }}$定义为第$\tau$段的词向量序列。值得一提的是，计算$A$矩阵的时候，需要对所有的$i-j$计算$W_{k,R}^n{R}_{i-j}$，如果直接按照公式计算的话，计算时间是$O(length{)}^2$，而实际上$i-j$的范围只从0 ~ length，因此可以先计算好这length个向量，然后在实际计算$A$矩阵时直接取用即可。

具体的，设$M$和$L$分别为memory和当前段序列的长度，则$i-j$的范围也就为0 ~ $M+L-1$。下面的$Q$矩阵中的每一行都代表着$W_{k,R}{R}_{i-j}$中一个$i-j$的可能性，即$Q_k=W_{k,R}{R}_{M+L-1-k}$。

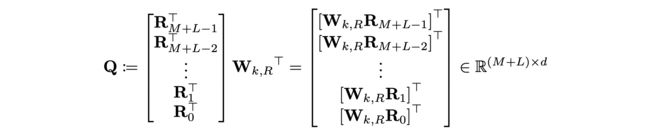
则对于上面公式中的(b)项，即$q_i^T{W}_{k,R}{R}_{i-j}$，其构成的所有可能向量的矩阵为$B$矩阵，其形状为$L\ast (M+L)$，这是我们最终需要的(b)项的attention结果。

我们进一步定义$\tilde{B}$矩阵为如下：

可见，需要的$B$矩阵的每一行只是$\tilde{B}$的向左shift而已。因此，可以直接利用矩阵乘法计算$\tilde{B}$即可。设$R_{i-j}$的维度为$d_R$，$q_i$的维度为$d_q$，$W_{k,R}$矩阵的维度为$d_q\ast d_R$，则直接计算矩阵B的时间复杂度为$2\ast d_q\ast d_R\ast L\ast (M+L)$，而计算$\tilde{B}$的时间复杂度为$L\ast d_q\ast (M+L)+d_q\ast d_R\ast (M+L)$，计算量明显不是一个量级（后者要快很多）。

同理，对于(d)项来说，可以对所有的$i-j$定义需要的矩阵$D$为$L\ast (M+L)$：

可以用如下的$\tilde{d}$来进行shift得到：

其中$Q$矩阵已经计算过了，也可以在这一步减少计算量。

四. PyTorch实现

笔者在这里主要研究的是核心模型部分，将针对关键的实现细节进行剖析，想要看完整代码的读者请戳这里。

1. 首先来看RelativePositionalEmbedding部分。

class PositionalEmbedding(nn.Module):
    def __init__(self, demb):
        super(PositionalEmbedding, self).__init__()
        self.demb = demb
        inv_freq = 1 / (10000 ** (torch.arange(0.0, demb, 2.0) / demb))

    def forward(self, pos_seq):
        sinusoid_inp = torch.ger(pos_seq, self.inv_freq)
        pos_emb = torch.cat([sinusoid_inp.sin(), sinusoid_inp.cos()], dim=-1)
        return pos_emb[:,None,:]

这里的demb是相对位置编码的维度，pos_seq是序列的位置向量，在代码里面是torch.arange(klen-1, -1, -1.0)，其中的klen是mlen+qlen，从名称和之前的原理介绍可知这里的mlen是memory的长度，qlen是query的长度，这两者组成了key的长度。最终返回的即是$R$向量矩阵，可见是不需要学习的。

2. 接着来看MultiHeadAttention的部分，为了叙述方便，这里的MultiHeadAttn是源代码中的RelMultiHeadAttn和RelPartialLearnableMultiHeadAttn的整合，也即一层self-attention的计算方式。

class MultiHeadAttn(nn.Module):
    def __init__(self, n_head, d_model, d_head, dropout, dropatt=0,
                 tgt_len=None, ext_len=None, mem_len=None, pre_lnorm=False):
        super(MultiHeadAttn, self).__init__()

		self.n_head = n_head
        self.d_model = d_model
        self.d_head = d_head
        self.dropout = dropout

        self.qkv_net = nn.Linear(d_model, 3 * n_head * d_head, bias=False)

        self.drop = nn.Dropout(dropout)
        self.dropatt = nn.Dropout(dropatt)
        self.o_net = nn.Linear(n_head * d_head, d_model, bias=False)

        self.layer_norm = nn.LayerNorm(d_model)

        self.scale = 1 / (d_head ** 0.5)

        self.pre_lnorm = pre_lnorm

        self.r_net = nn.Linear(self.d_model, self.n_head * self.d_head, bias=False)

		def _rel_shift(self, x, zero_triu=False):
	        zero_pad = torch.zeros((x.size(0), 1, *x.size()[2:]),
	                               device=x.device, dtype=x.dtype)
	        x_padded = torch.cat([zero_pad, x], dim=1)
	
	        x_padded = x_padded.view(x.size(1) + 1, x.size(0), *x.size()[2:])
	
	        x = x_padded[1:].view_as(x)
	
	        if zero_triu:
	            ones = torch.ones((x.size(0), x.size(1)))
	            x = x * torch.tril(ones, x.size(1) - x.size(0))[:,:,None,None]
	
	        return x

        def forward(self, w, r, r_w_bias, r_r_bias, attn_mask=None, mems=None):
	        qlen, rlen, bsz = w.size(0), r.size(0), w.size(1)
	
	        if mems is not None:
	            cat = torch.cat([mems, w], 0)
	            if self.pre_lnorm:
	                w_heads = self.qkv_net(self.layer_norm(cat))
	            else:
	                w_heads = self.qkv_net(cat)
	            r_head_k = self.r_net(r)
	
	            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1)
	            w_head_q = w_head_q[-qlen:]
	        else:
	            if self.pre_lnorm:
	                w_heads = self.qkv_net(self.layer_norm(w))
	            else:
	                w_heads = self.qkv_net(w)
	            r_head_k = self.r_net(r)
	
	            w_head_q, w_head_k, w_head_v = torch.chunk(w_heads, 3, dim=-1)
	
	        klen = w_head_k.size(0)
	
	        w_head_q = w_head_q.view(qlen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	        w_head_k = w_head_k.view(klen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	        w_head_v = w_head_v.view(klen, bsz, self.n_head, self.d_head)           # qlen x bsz x n_head x d_head
	
	        r_head_k = r_head_k.view(rlen, self.n_head, self.d_head)                # qlen x n_head x d_head
	
	        #### compute attention score
	        rw_head_q = w_head_q + r_w_bias                                         # qlen x bsz x n_head x d_head
	        AC = torch.einsum('ibnd,jbnd->ijbn', (rw_head_q, w_head_k))             # qlen x klen x bsz x n_head
	
	        rr_head_q = w_head_q + r_r_bias
	        BD = torch.einsum('ibnd,jnd->ijbn', (rr_head_q, r_head_k))              # qlen x klen x bsz x n_head
	        BD = self._rel_shift(BD)
	
	        # [qlen x klen x bsz x n_head]
	        attn_score = AC + BD
	        attn_score.mul_(self.scale)
	
	        #### compute attention probability
	        if attn_mask is not None and attn_mask.any().item():
	            if attn_mask.dim() == 2:
	                attn_score = attn_score.float().masked_fill(
	                    attn_mask[None,:,:,None], -float('inf')).type_as(attn_score)
	            elif attn_mask.dim() == 3:
	                attn_score = attn_score.float().masked_fill(
	                    attn_mask[:,:,:,None], -float('inf')).type_as(attn_score)
	
	        # [qlen x klen x bsz x n_head]
	        attn_prob = F.softmax(attn_score, dim=1)
	        attn_prob = self.dropatt(attn_prob)
	
	        #### compute attention vector
	        attn_vec = torch.einsum('ijbn,jbnd->ibnd', (attn_prob, w_head_v))
	
	        # [qlen x bsz x n_head x d_head]
	        attn_vec = attn_vec.contiguous().view(
	            attn_vec.size(0), attn_vec.size(1), self.n_head * self.d_head)
	
	        ##### linear projection
	        attn_out = self.o_net(attn_vec)
	        attn_out = self.drop(attn_out)
	
	        if self.pre_lnorm:
	            ##### residual connection
	            output = w + attn_out
	        else:
	            ##### residual connection + layer normalization
	            output = self.layer_norm(w + attn_out)
	
	        return output

其中n_head，d_model，d_head分别表示注意力头的个数，模型的隐层维度，每个头的隐层维度。qkv_net是用于计算query、key和value变换的参数矩阵$W_q,W_{k,E},W_v$，与标准的Transformer中一致，o_net是用于将所有注意力头的结果拼接后再变换到模型维度的参数矩阵，layer_norm是LayerNormalization层，r_net是用于计算relative position embedding变换的参数矩阵$W_{k,R}$。

在前向计算的过程中，w和r分别是上一层的输出以及RelativePositionEmbedding，r_w_bias和r_r_bias分别是$u$向量和$v$向量，AC是前面公式中的（a）项和（c）项，BD是前面公式中的（b）项和（d）项，根据前面讲的快速计算带有相对位置的项，这里的BD需要进行偏移，即_rel_shift，经过笔者的演算，发现这里经过此函数后的BD并不是想要的$B$矩阵，其在$B$矩阵的(M+1)对角线（设主对角线为0，正数即为向右上偏移的量）的右上还有元素，不过后面紧接着就进行了mask。这里的attn_mask即为torch.triu(word_emb.new_ones(qlen, klen), diagonal=1+mlen).byte()[:,:,None]。再往后就是标准的Transformer中的add&norm环节了，就不再赘述。

3. 最后来看memory的更新过程：

def _update_mems(self, hids, mems, qlen, mlen):
    # does not deal with None
    if mems is None: return None

    # mems is not None
    assert len(hids) == len(mems), 'len(hids) != len(mems)'

    # There are `mlen + qlen` steps that can be cached into mems
    # For the next step, the last `ext_len` of the `qlen` tokens
    # will be used as the extended context. Hence, we only cache
    # the tokens from `mlen + qlen - self.ext_len - self.mem_len`
    # to `mlen + qlen - self.ext_len`.
    with torch.no_grad():
        new_mems = []
        end_idx = mlen + max(0, qlen - 0 - self.ext_len)
        beg_idx = max(0, end_idx - self.mem_len)
        for i in range(len(hids)):

            cat = torch.cat([mems[i], hids[i]], dim=0)
            new_mems.append(cat[beg_idx:end_idx].detach())

    return new_mems

这里的hids是当前段每层的输出，mems为当前段每层依赖的memory，qlen为序列长度，mlen为当前段依赖的memory的长度。

从代码来看的话，前面的循环示意图似乎有些问题？感觉在训练阶段，对于每个段里面的第二个位置开始的点，都应该连到第一个位置连到的最前面memory？因为用的是同样长度的memory。

五. 实验结果

1. 语言建模指标

在最关心的语言模型建模指标上，论文比较了模型在单词级别和字符级别上不同数据集的表现，并且与RNN和(vanilla) Transformer都做了比较。实验证明，Transformer-XL在各个不同的数据集上均实现了目前的SoTA：在大型单词级别数据集WikiText-103上，Transformer-XL将困惑度从20.5降到18.3；在enwiki8数据集上，12层Transformer-XL的bpc达到了1.06，相同bpc的AI-Rfou的模型（ https://arxiv.org/abs/1808.04444 )参数量却是6倍，24层Transformer-XL的bpc更是达到了0.99；在One Billion Word数据集上（仅具有短句的）和Penn Treebank数据集上（小型，仅有1M）也取得了SoTA的效果，前者的困惑度从23.7到21.8，后者的困惑度从55.3到54.5。表明了Transformer-XL在各个数据集下的不俗竞争力。

2. 两个创新点的优势

下图比较了不同上下文长度（即memory的长度）中包不包含循环机制、以及使不使用新位置编码方式的困惑度得分。可见，使用循环机制和相对位置编码的Transformer-XL明显优于其他的模型，并且能够有效利用长期依赖性，而且它能捕获超出RNN 80%的依赖性，和超出Transformer 450%的依赖性。

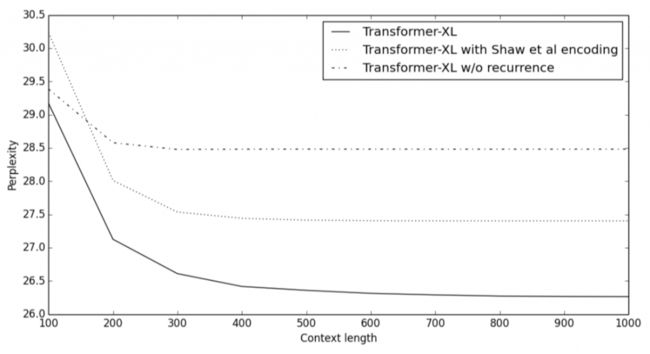
3. 测试阶段的速度

Transformer-XL的推理速度也明显快于vanilla Transformer，尤其是对于较长的上下文。比如，在上下文长度为800时，Transformer-XL提速363倍；而当上下文长度增加到3800时，Transformer-XL提速1874倍！

六. 总结

1. 模型特点

在 AI-Rfou 等人提出的vanilla Transformer上做了两点创新：

1. 引入循环机制（Recurrence Mechanism）
2. 相对位置编码（Relative Positional Encoding）

2. 优点

1. 在几种不同的数据集（大/小，字符级别/单词级别等）均实现了最先进的语言建模结果。
2. 结合了深度学习的两个重要概念——循环机制和注意力机制，允许模型学习长期依赖性，且可能可以扩展到需要该能力的其他深度学习领域，例如音频分析（如每秒16k样本的语音数据）等。
3. 在inference阶段非常快，比之前最先进的利用Transformer模型进行语言建模的方法快300～1800倍。
4. 有详尽的源码！含TensorFlow和PyTorch版本的，并且有TensorFlow预训练好的模型及各个数据集上详尽的超参数设置。

3. 不足

1. 尚未在具体的NLP任务如情感分析、QA等上应用。
2. 没有给出与其他的基于Transformer的模型，如BERT等，对比有何优势。
3. 在Github源码中提到，目前的sota结果是在TPU大集群上训练得出，对于我等渣机器党就只能玩玩base模式了。

传送门

论文：https://arxiv.org/pdf/1901.02860.pdf
代码：https://github.com/kimiyoung/transformer-xl
参考：https://www.lyrn.ai/2019/01/16/transformer-xl-sota-language-model