Chapter 8 无监督学习与数据降维 (reading notes)

0. 版权声明

• machine learning 系列笔记来源于Andrew Ng 教授在 Coursera 网站上所授课程《machine learning》¹；
• 该系列笔记不以盈利为目的，仅用于个人学习、课后复习及交流讨论；
• 如有侵权，请与本人联系（[email protected]），经核实后即刻删除；
• 转载请注明出处；

1. Unsupervised learning

• 无监督学习：聚类、降维、异常检测 … …；

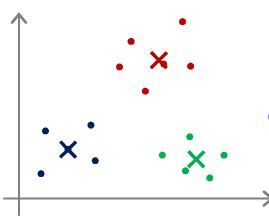
1.1 Clustring（聚类）

• 聚类中用到的符号:
  • K：大写的 K 表示簇的数量，即聚类中心的数量；
  • k：小写的 k 表示不同聚类中心的下标；
  • $c^{(i)}$：样本 $x^{(i)}$ 所在簇的索引；
  • $u_k$：第 k 个聚类中心的位置；
  • $u_{c^{(i)}}$：样本 $x^{(i)}$ 所在簇的聚类中心的位置；
• 数据降维中用到的符号：
  • k：主成分的数量；
  • $z^{(i)}$：数据降维后的第 i 个样本点；
• 聚类算法有：K-means 算法（K均值算法）。。。；
• K-means 算法的输入：
  • K：簇的数量；
  • 训练集：$\{x^1,x^2,...,x^m\}$；
    • $x^{(i)}\in {\mathbb{R}}^n$，因为按照惯例，此处 drop $x_0=1$；
• K-means 算法步骤：
  • 随机初始化 K 个聚类中心 $u_1,u_2,...,u_k\in {\mathbb{R}}^n$；
  • 簇分配：按照距离远近，将各个样本匹配到最近的聚类中心；
    • 求解 $min||x^{(i)}-u_k|{|}^2$ 或 $\underset{k}{\min }||x^{(i)}-u_k||$；
    • 该步骤用于优化 $c^{(1)},c^{(2)},...,c^{(m)}$；
  • 移动聚类中心：根据簇分配得到的本类别的样本点均值，求得新的聚类中心；
    • 该步骤用于优化 $u_1,u_2,...,u_K$；
• Q：若在簇分配阶段，有的簇没有被分配任何样本点，应如何处理？
  A：
  • 若不严格要求将样本划分为 K 个簇，则直接去掉该簇；
  • 若严格要求将样本划分为 K 个簇，则再随机选取一个聚类中心，替换掉未被分配样本点的簇；

1.2 优化目标

• 代价函数：$J(c^{(1)},c^{(2)},...,c^{(m)},u_1,u_2,...,u_K)=\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-u_{c^{(i)}}|{|}^2$；
  • 该代价函数被称为失真代价函数，或 K 均值算法的失真；
  • 代价函数的意义：最小化各个样本点到对应聚类中心的距离；

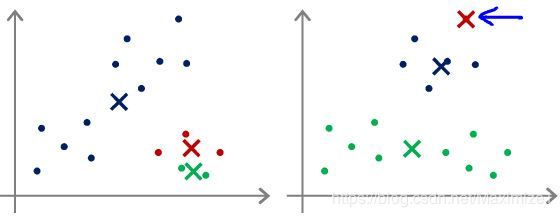
1.3 随机初始化

• 随机初始化状态不同，可能导致 K 均值算法得到的运算结果不同；

  • Soultion：多次随机初始化（典型的次数为50-1000次），选取代价函数最小的聚类结果；
  • 若 K 的数值较小（在2-10之间），使用多次随机初始化的方法一般能够得到较好的局部最优解；
  • 若 K 的数值较大（远大于10），K-means 算法仍能给出一个合适的结果，但该状态下使用多次随机初始化对结果的改善不明显；
    

• K-means 算法随机初始化的方法：

  • 确保簇的数量小于样本数量，即 K
  • 随机从选择 K 个样本作为聚类中心；

• Q：一般而言，K 取值越大时，代价函数越小，若 K=5 时的代价高于 K=3 时的代价，可能的原因是什么？
  A：K=5时，运行 K-means 算法得到了一个较差的局部最小值；可尝试多次随机初始化加以解决；

1.4 选择聚类数量 K 的方法

• 选择聚类数量 K 的方法：
  • 手动选择：最为常见的方法，根据实际问题的需要，选择合适的 K 值；
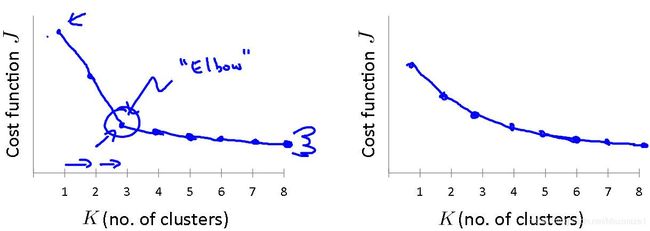
  • Elbow method（肘部法则）：一种用于选择聚类数量 K 的方法；
    • 若代价函数的导数值变化出现明显的拐点，则取该点对应的簇数量作为 K 值；
    • 若代价函数的导数值变化无明显的拐点，则该方法不适用；

2. 数据降维

2.1 数据压缩与可视化

• 数据压缩的作用：
  • 减小数据冗余，从而减小数据占用的存储空间；
  • 加快机器学习算法运行速度，使算法更快收敛；
  • 便于可视化；
    • 至多只能做三维数据的可视化；
• $z^{(i)}$：降维后的第 i 个样本点；

2.2 Principal component analysis（PCA，主成分分析）

2.2.1 PCA 的数学含义

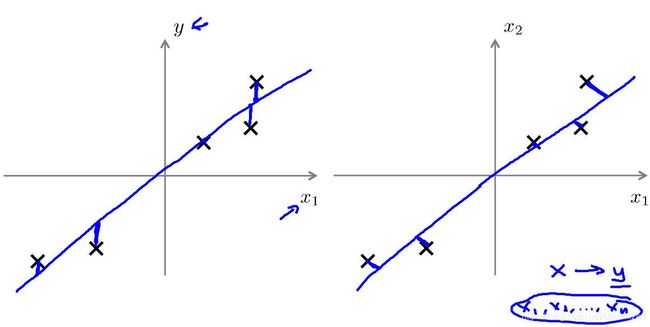
• PCA 的数学本质：寻找一个数据平面，使各样本投影误差的平方和最小；
  • 投影误差：样本点与投影点的间距；
  • e.g. 将数据从三维降到二维，寻找一个非零向量 $u^{(1)}\in {\mathbb{R}}^2$，使得各样本点向该向量所在直线做投影，所得投影误差的平方和最小；
  • e.g. 将数据从 n 维降到 k 维，寻找 k 个非零向量 $u^{(1)},u^{(2)},...,u^{(k)}\in {\mathbb{R}}^n$，使得各样本点向 k 个向量展开的线性子空间做投影，所得投影误差的平方和最小；
• Q：线性回归与 PCA 的不同之处？
  A：
  • 线性回归的优化目标：使预测值与真实值之间误差的平方和最小；
  • PCA 的优化目标：使各样本投影误差的平方和最小；
  • 下图中左侧为线性回归的优化目标，指预测值与真实值在 y 轴方向的间距；
    下图中右侧为 PCA 的优化目标，指样本点与投影点的间距；
    

2.2.2 PCA 的算法实现

• 执行 PCA 之前的数据预处理：
  • 先进行均值归一化（mean normalization），使各特征均值为0；
  • 根据各特征的量级选择是否使用特征缩放（feature scaling）；
  • 均值归一化、特征缩放均与监督学习中的操作步骤相同；
• PCA 算法：
  • step1：求协方差矩阵 $\Sigma =\frac{1}{m}{\sum }_{i=1}^n(x^{(i)})(x^{(i)}{)}^T$；
    • 上式中等号左侧的 $\Sigma$ 为大写的 Sigma ，代表协方差；等号右侧的 $\Sigma$ 为求和符号，两者含义不同；
    • 假定将求得的协方差矩阵 $\Sigma$ 存储在变量 Sigma 中；
    • $x^{(i)}$ 为 n 维向量， $\Sigma$ 为 $n\times n$ 矩阵；
    • 可使用向量化的方式求解协方差矩阵：
      • 若 X 为 $m\times n$ 矩阵，每行表示一个样本，故需将每个样本转换为列向量代入计算， $X^T(X^T{)}^T=X^{T}X$，则 $\Sigma =\frac{X^{T}X}{m}$；
  • step2：求协方差矩阵 $\Sigma$ 的特征向量：
    • [U, S, V] = svd(Sigma); 或 [U, S, V] = eig(Sigma);；
    • 在Octave 中可使用上述语句求解特征向量，两者所求结果相同，但 svd() 函数更加稳定；
    • svd(singular value decomposition)：奇异值分解；
    • $U=\left[\begin{array}{cccc}|& |& & |\\ u^{(1)}& u^{(2)}& \cdot \cdot \cdot & u^{(n)}\\ |& |& & |\end{array}\right]\in {\mathbb{R}}^{n\times n}$；
      • 若需将数据从 n 维降到 k 维，则取矩阵 U 的前 k 列即为 $u^{(1)},u^{(2)},...,u^{(k)}$，记为 $U_{reduce}=\left[\begin{array}{cccc}|& |& & |\\ u^{(1)}& u^{(2)}& \cdot \cdot \cdot & u^{(k)}\\ |& |& & |\end{array}\right]$；
      • $z^{(i)}={\left[\begin{array}{cccc}|& |& & |\\ u^{(1)}& u^{(2)}& \cdot \cdot \cdot & u^{(k)}\\ |& |& & |\end{array}\right]}^T{x}^{(i)}=\left[\begin{array}{ccc}-& (u^{(1)}{)}^T& -\\ -& (u^{(2)}{)}^T& -\\ & ⋮& \\ -& (u^{(k)}{)}^T& -\end{array}\right]x^{(i)}$ ；
        • $U_{reduce}$ 为 $n\times k$ 矩阵，$x^{(i)}$ 为 n 维向量，$z^{(i)}$ 为 k 维向量；
        • 此处 $x^{(i)}$ 不含 $x_0$；
      • 向量化有 $Z={\left[\begin{array}{cccc}|& |& & |\\ u^{(1)}& u^{(2)}& \cdot \cdot \cdot & u^{(k)}\\ |& |& & |\end{array}\right]}^{T}X=\left[\begin{array}{ccc}-& (u^{(1)}{)}^T& -\\ -& (u^{(2)}{)}^T& -\\ & ⋮& \\ -& (u^{(k)}{)}^T& -\end{array}\right]X=U_{reduce}^{T}X$ ；

3. 应用 PCA 算法

3.1 数据重构

• $x_{approx}^{(i)}=U_{reduce}\cdot z^{(i)}$；
  • $U_{reduce}$ 为 $n\times k$ 矩阵，$z^{(i)}$ 为 k 维向量，$x_{approx}^{(i)}$ 为 n 维向量；
  • 数据重构后所得的 $x_{approx}^{(i)}$ 接近于 $x^{(i)}$；

3.2 选择主成分的数量 k

• 选择 k 的依据：
  • 平均平方投影误差（average squared projection error）：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2$；
  • 总变差（total variance）：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2$；
    • Total variance 的含义：各样本整体上距离原点有多远；
• 一个常见的选择 k 值得经验法则：$\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}\le 0.01$；
  • 等式右侧数值的含义：99%的变量信息得到了保留；
  • 等式右侧常用的取值有0.01、0.05，此外还有0.10、0.15等；
  • 选取满足该不等式的最小 k 值；
• 算法实现：
  • [U, S, V] = svd(Sigma); 或 [U, S, V] = eig(Sigma);；
    • 上述语句中，S 为 $n\times n$ 对角矩阵，$S=\left[\begin{array}{ccccc}{S}_{11}& & & & \\ & S_{22}& & & \\ & & S_{33}& & \\ & & & \ddots & \\ & & & & S_{nn}\end{array}\right]$；
    • 且有 $\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}=1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}$；
  • step1：分别取 $k=1,2,...,n$；
  • step2：分别计算 $U_{reduce},z^{(1)},z^{(2)},...,z^{(m)},x_{approx}^{(1)},...,x_{approx}^{(m)}$；
  • step3：检查是否满足 $\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}=1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}\le 0.01$，取满足该条件的最小 k 值；

3.3 应用 PCA 的建议

• $z^{(i)}$：在训练集中应用 PCA 求得，在交叉验证集和测试集中取对应 $z^{(i)}$ 即可，而不可在交叉验证集和测试集中应用 PCA 求 $z^{(i)}$；
• PCA 不宜用于避免过拟合；
  • PCA 会在不考虑 y 值得情况下，去除部分特征，将导致信息丢失；
  • 正则化用于防止过拟合效果更好；
• 在设计机器学习系统时，先使用原始数据求解，若出现收敛缓慢或大量占用内存、硬盘空间时，再考虑使用 PCA；
  • 不可在系统设计之初就预先考虑 PCA，没有使用依据，即为无用步骤；

n. Reference

---

1. https://www.coursera.org/learn/machine-learning/home/welcome ↩︎