算法日记本 | LeetCode 42. 接雨水
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
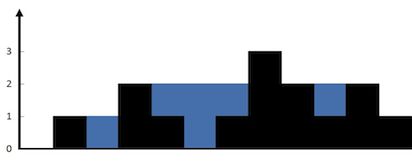
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
分析解答
这是一道非常生活化的题目,乍一看感觉无从下手。那我们就仔细分析下题目,什么时候才可以接到雨水呢?没错,就是当中间一根柱子比旁边两根都低的时候。如果我们先找到最高的那根柱子H,那么对于H左边的柱子A来说,只要A的高度低于它左边已经出现过的最高的柱子就可以接到雨水,因为右边有最高的柱子H在顶着;同样的,对于H右边的柱子B来说,只要B的高度低于它右边已经出现过的最高的柱子就可以接到雨水。我们可以在遍历过程中更新当前遇到的最高的柱子。按照这种思路实现的代码如下:
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
n = len(height)
if n <= 2:
return 0
# 寻找最高的柱子
max_height = height[0]
max_idx = 0
for i in range(1, n):
if height[i] > max_height:
max_height = height[i]
max_idx = i
# 从左右两边分别朝最高的柱子遍历
res = 0
max_height_left = 0
for i in range(max_idx):
max_height_left = max(height[i], max_height_left)
res += (max_height_left - height[i])
max_height_right = 0
for i in range(n - 1, max_idx, -1):
max_height_right = max(height[i], max_height_right)
res += (max_height_right - height[i])
return res
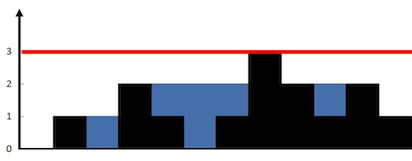
上面这种方法很直观,容易理解,缺点是需要遍历数组两次。如果我们再仔细观察示例中的图片,雨水的数量其实就是蓝色部分的面积,既然是求面试可不可以用一种更数学的方式来做的。比如,我们在最高的柱子上加一条线,示例图片就成了下面这样:
为了方便描述,我们把蓝色部分面积记作A,黑色部分记作B,红线下方左边白色部分记作C,右边白色部分记作D,整个大矩形(红线以下部分)的面积H已知。大家有没有发现这个很像是我们小学时候做的脑筋急转弯的题目的?下面我来写几个公式:
A + B + C + D = H
(A + B + C) + (A + B + D) = H + A + B
A = H + A + B - H - B
是不是觉得有点二,哈哈,下面我逐个来解释。第一个公式很简单,4个小块的面积等于整个大块的面积。第二个公式也很简单,但问题是为什么要这么写呢?这是该解法最讨巧的地方,A+B+C的面积其实可以通过从左遍历数组对当前最大高度求和得到。同理,A+B+D的面积可以通过从右遍历数组对当前最大高度求和得到。有了这两个之后,再结合公式三,只要减去整个矩形面积H和B即可,H就是数组的长度乘以最大高度,B就是全部柱子的高度之和,两个都很容易求得。还有一个优化的点,我们可以只对数组做一次遍历,同时求当前左边最大高度和右边最大高度。按照这种思路实现的代码如下:
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
# 一次遍历 借助集合的交并补思想
n = len(height)
area = 0
max_height_left, max_height_right = 0, 0
for i in range(n):
max_height_left = max(max_height_left, height[i])
max_height_right = max(max_height_right, height[-i - 1])
area = area + max_height_left + max_height_right - height[i]
return area - n * max_height_left
相比解法一来说简洁了很多,理解之后会很容易记住哦。
好啦,以上就是今天的分享。我们下期再见!