bzoj4964: 加长的咒语

求区间最长匹配的括号序列子串。

很有意思的括号，但是我有些细节没处理好，导致代码长，算法复杂。。 如果有更好的算法我也很想知道啊>.<

考虑一个括号序列A=(B1)(B2)(B3)…，其中与某个括号匹配的相对的括号唯一。证明显然。

有一个显然的算法：用栈判断一个字符串是否为括号序列。

考虑拓展这个结论：对任意括号串的某个括号序列子串，某个括号匹配的相对的括号唯一。证明显然。

既然这样就随便建一些（）树，每个节点表示一对匹配的括号，儿子表示在这对括号中的括号序列。

不妨只考虑询问在同一颗（）树的（节点~）节点的答案。

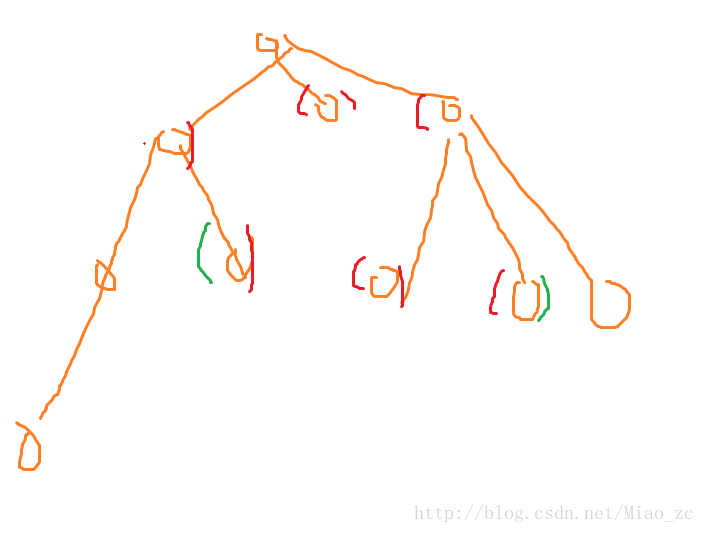
如图，询问绿括号的答案，令u，v是深度大于lca的最浅的x，y的祖先。那么（u，v）这一段都可以作为答案。对于答案不在这之中的情况，考虑选绿括号和不选绿括号。

选的方案容易得到，不选的方案相当于链上最大值。于是可以在O(nlogn+qlogn)的时间内得到答案。

如果是长链剖分可以达到O(nlogn+q)的毒瘤复杂度。

算法瓶颈在于寻找uv，不知道有没有更好的做法。

这里有claris的题解

似乎这种括号匹配还能离线做，可以思考一下，想出来再更新吧。。

#include
#define N 400005
using namespace std;
int n,q,id[N],l[N],r[N],lt[N],rt[N],fl[N],fr[N];
int Rt[N],ly,f[N];
int fa[N][25],dep[N],v[N][25],vl[N][25],vr[N][25],cnt;
int st[N],top;
char s[N];
void build(int k,int L,int R)
{
	for (int i=2,j=1;i<=dep[k];i<<=1,j++)
	{
		fa[k][j]=fa[fa[k][j-1]][j-1];
		vl[k][j]=max(vl[k][j-1],vl[fa[k][j-1]][j-1]);
		vr[k][j]=max(vr[k][j-1],vr[fa[k][j-1]][j-1]);
	}
	if (L>R) return;
	int t=L;
	for (;L<=R;L=r[L]+1)
	{
		fa[++cnt][0]=k;
		dep[cnt]=dep[k]+1;
		f[cnt]=f[k];
		vl[cnt][0]=R-r[L];
		vr[cnt][0]=L-t;
		id[L]=cnt;id[r[L]]=cnt;
		lt[cnt]=L;
		rt[cnt]=r[L];
		build(cnt,L+1,r[L]-1);
	}
}
int lg[N];
int qry(int x,int y)
{
	if (x>y) return 0;
	int len=y-x+1,tmp=lg[len];
	return max(v[x][tmp],v[y-(1<>1]+1;
	for (int i=1;i<=lg[ly];i++)
	for (int j=1;j<=n-(1<=1;i--)
	{
		if (r[i]) t=i;
		fr[i]=t;
	}
	
	for (int i=1;i<=q;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		x=fr[x];
		y=fl[y];
		if (x>y) puts("0");
		else
		{
			int t1,t2,Ans=0;
			if (id[x]==id[y]) Ans=y-x+1;
			else
			{
			x=id[x];y=id[y];
			if (f[x]==f[y])
			{
				if (dep[x]>dep[y])
				{
					Ans=max(Ans,rt[fa[x][0]]-lt[x]);
					t1=1<<20;t2=20;
					for (;t2>=0;t1>>=1,t2--)
					{
						if (t1>dep[x]-dep[y])continue;
						Ans=max(Ans,vl[x][t2]);
						x=fa[x][t2];
					}
					Ans=max(Ans,rt[y]-max(lt[fa[y][0]],rt[x]));
				}
				else if (dep[x]=0;t1>>=1,t2--)
					{
						if (t1>dep[y]-dep[x])continue;
						Ans=max(Ans,vr[y][t2]);
						y=fa[y][t2];
					}
					Ans=max(Ans,min(rt[fa[x][0]],lt[y])-lt[x]);
				}
				else
				{
					Ans=max(Ans,rt[y]-max(lt[fa[y][0]],lt[x]-1));
					Ans=max(Ans,min(rt[fa[x][0]],rt[y]+1)-lt[x]);
				}
				t1=1<<20;t2=20;
				for (;t2>=0;t1>>=1,t2--)
				{
					if (t1>dep[x]||fa[x][t2]==fa[y][t2])continue;
					Ans=max(Ans,vl[x][t2]);
					Ans=max(Ans,vr[y][t2]);
					x=fa[x][t2];
					y=fa[y][t2];
				}
				Ans=max(Ans,lt[y]-rt[x]-1);
			}
			else
			{
				Ans=max(Ans,rt[fa[x][0]]-lt[x]);
				Ans=max(Ans,rt[y]-lt[fa[y][0]]);
				t1=1<<20;t2=20;
				for (;t2>=0;t1>>=1,t2--)
				{
					if (t1>dep[x])continue;
					Ans=max(Ans,vl[x][t2]);
					x=fa[x][t2];
				}
				t1=1<<20;t2=20;
				for (;t2>=0;t1>>=1,t2--)
				{
					if (t1>dep[y])continue;
					Ans=max(Ans,vr[y][t2]);
					y=fa[y][t2];
				}
				Ans=max(Ans,qry(f[x]+1,f[y]-1));
			}
		}
			printf("%d\n",Ans);
		}
	}
}