Tensorflow中计算图机制和常用函数笔记
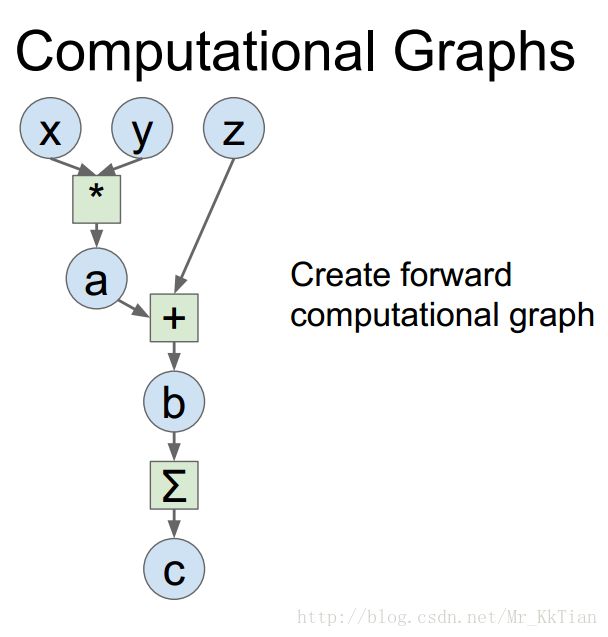
0计算图机制
程序如下:
#basic computational graph
import numpy as np
np.random.seed(0)
import tensorflow as tf
N, D =3, 4
x=tf.placeholder(tf.float32)
y=tf.placeholder(tf.float32)
z=tf.placeholder(tf.float32)
a=x*y
b=a+z
c=tf.reduce_sum(b)
grad_x,grad_y,grad_z=tf.gradients(c,[x,y,z])
with tf.Session() as sess:
values={
x:np.random.randn(N,D),
y:np.random.randn(N,D),
z:np.random.randn(N,D),
}
out=sess.run([c,grad_x,grad_y,grad_z],feed_dict=values)
c_val,grad_x_val,grad_y_val,grad_z_val=out
print("c_val= %d"%(c_val))
print("grad_x_val=")
print(grad_x_val)
1 tf.layers.dense()全连接层
dense(inputs, units, activation=None, use_bias=True, kernel_initializer=None, bias_initializer=, kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, trainable=True, name=None, reuse=None)
Functional interface for the densely-connected layer.
This layer implements the operation:
`outputs = activation(inputs.kernel + bias)`
Where `activation` is the activation function passed as the `activation`
argument (if not `None`), `kernel` is a weights matrix created by the layer,
and `bias` is a bias vector created by the layer
(only if `use_bias` is `True`).
Note: if the `inputs` tensor has a rank greater than 2, then it is
flattened prior to the initial matrix multiply by `kernel`.
Arguments:
inputs: Tensor input.
units: Integer or Long, dimensionality of the output space.
activation: Activation function (callable). Set it to None to maintain a
linear activation.
use_bias: Boolean, whether the layer uses a bias.
kernel_initializer: Initializer function for the weight matrix.
bias_initializer: Initializer function for the bias.
kernel_regularizer: Regularizer function for the weight matrix.
bias_regularizer: Regularizer function for the bias.
activity_regularizer: Regularizer function for the output.
trainable: Boolean, if `True` also add variables to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see `tf.Variable`).
name: String, the name of the layer.
reuse: Boolean, whether to reuse the weights of a previous layer
by the same name.
Returns:
Output tensor.
2 tf.nn.tanh()
tanh(x, name=None)
Computes hyperbolic tangent of `x` element-wise.//计算x的双曲正切值
Args:
x: A Tensor or SparseTensor with type `float`, `double`, `int32`,
`complex64`, `int64`, or `qint32`.
name: A name for the operation (optional).
Returns:
A Tensor or SparseTensor respectively with the same type as `x` if
`x.dtype != qint32` otherwise the return type is `quint8`.
3 tf.reshape()
reshape(tensor, shape, name=None)
Reshapes a tensor.
Given `tensor`, this operation returns a tensor that has the same values
as `tensor` with shape `shape`.
If one component of `shape` is the special value -1, the size of that dimension
is computed so that the total size remains constant. In particular, a `shape`
of `[-1]` flattens into 1-D. At most one component of `shape` can be -1.
If `shape` is 1-D or higher, then the operation returns a tensor with shape
`shape` filled with the values of `tensor`. In this case, the number of elements
implied by `shape` must be the same as the number of elements in `tensor`.
For example:
```
# tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
# tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
# tensor 't' is [[[1, 1], [2, 2]],
# [[3, 3], [4, 4]]]
# tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],
[3, 3, 4, 4]]
# tensor 't' is [[[1, 1, 1],
# [2, 2, 2]],
# [[3, 3, 3],
# [4, 4, 4]],
# [[5, 5, 5],
# [6, 6, 6]]]
# tensor 't' has shape [3, 2, 3]
# pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6]
4 tf.layers.conv2d_transpose()
conv2d_transpose(inputs, filters, kernel_size, strides=(1, 1), padding='valid', data_format='channels_last', activation=None, use_bias=True, kernel_initializer=None, bias_initializer=, kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, trainable=True, name=None, reuse=None)
Functional interface for transposed 2D convolution layer.
The need for transposed convolutions generally arises
from the desire to use a transformation going in the opposite direction
of a normal convolution, i.e., from something that has the shape of the
output of some convolution to something that has the shape of its input
while maintaining a connectivity pattern that is compatible with
said convolution.
Arguments:
inputs: Input tensor.
filters: Integer, the dimensionality of the output space (i.e. the number
of filters in the convolution).
kernel_size: A tuple or list of 2 positive integers specifying the spatial
dimensions of of the filters. Can be a single integer to specify the same
value for all spatial dimensions.
strides: A tuple or list of 2 positive integers specifying the strides
of the convolution. Can be a single integer to specify the same value for
all spatial dimensions.
padding: one of `"valid"` or `"same"` (case-insensitive).
data_format: A string, one of `channels_last` (default) or `channels_first`.
The ordering of the dimensions in the inputs.
`channels_last` corresponds to inputs with shape
`(batch, height, width, channels)` while `channels_first` corresponds to
inputs with shape `(batch, channels, height, width)`.
activation: Activation function. Set it to `None` to maintain a
linear activation.
use_bias: Boolean, whether the layer uses a bias.
kernel_initializer: An initializer for the convolution kernel.
bias_initializer: An initializer for the bias vector. If `None`, then no
bias will be applied.
kernel_regularizer: Optional regularizer for the convolution kernel.
bias_regularizer: Optional regularizer for the bias vector.
activity_regularizer: Regularizer function for the output.
trainable: Boolean, if `True` also add variables to the graph collection
5 tf.nn.sigmoid()
sigmoid(x, name=None)
Computes sigmoid of `x` element-wise.
Specifically, `y = 1 / (1 + exp(-x))`.
Args:
x: A Tensor with type `float32`, `float64`, `int32`, `complex64`, `int64`,
or `qint32`.
name: A name for the operation (optional).
Returns:
A Tensor with the same type as `x` if `x.dtype != qint32`
otherwise the return type is `quint8`.
@compatibility(numpy)
Equivalent to np.scipy.special.expit
@end_compatibility
6 tf.layers.conv2d()
conv2d(inputs, filters, kernel_size, strides=(1, 1), padding='valid', data_format='channels_last', dilation_rate=(1, 1), activation=None, use
_bias=True, kernel_initializer=None, bias_initializer=, kernel_regularizer=None, bias_regularize
r=None, activity_regularizer=None, trainable=True, name=None, reuse=None)
Functional interface for the 2D convolution layer.
This layer creates a convolution kernel that is convolved
(actually cross-correlated) with the layer input to produce a tensor of
outputs. If `use_bias` is True (and a `bias_initializer` is provided),
a bias vector is created and added to the outputs. Finally, if
`activation` is not `None`, it is applied to the outputs as well.
Arguments:
inputs: Tensor input.
filters: Integer, the dimensionality of the output space (i.e. the number
of filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the
width and height of the 2D convolution window.
Can be a single integer to specify the same value for
all spatial dimensions.
strides: An integer or tuple/list of 2 integers,
specifying the strides of the convolution along the height and width.
Can be a single integer to specify the same value for
all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying
any `dilation_rate` value != 1.
padding: One of `"valid"` or `"same"` (case-insensitive).
data_format: A string, one of `channels_last` (default) or `channels_first`.
The ordering of the dimensions in the inputs.
`channels_last` corresponds to inputs with shape
`(batch, height, width, channels)` while `channels_first` corresponds to
inputs with shape `(batch, channels, height, width)`.
dilation_rate: An integer or tuple/list of 2 integers, specifying
the dilation rate to use for dilated convolution.
Can be a single integer to specify the same value for
all spatial dimensions.
Currently, specifying any `dilation_rate` value != 1 is
incompatible with specifying any stride value != 1.
activation: Activation function. Set it to None to maintain a
linear activation.
use_bias: Boolean, whether the layer uses a bias.
kernel_initializer: An initializer for the convolution kernel.
bias_initializer: An initializer for the bias vector. If None, no bias will
be applied.
kernel_regularizer: Optional regularizer for the convolution kernel.
bias_regularizer: Optional regularizer for the bias vector.
activity_regularizer: Regularizer function for the output.
trainable: Boolean, if `True` also add variables to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see `tf.Variable`).
name: A string, the name of the layer.
reuse: Boolean, whether to reuse the weights of a previous layer
by the same name.
Returns:
Output tensor.
7 tf.layers.average_pooling2d()
average_pooling2d(inputs, pool_size, strides, padding='valid', data_format='channels_last', name=None)
Average pooling layer for 2D inputs (e.g. images).
Arguments:
inputs: The tensor over which to pool. Must have rank 4.
pool_size: An integer or tuple/list of 2 integers: (pool_height, pool_width)
specifying the size of the pooling window.
Can be a single integer to specify the same value for
all spatial dimensions.
strides: An integer or tuple/list of 2 integers,
specifying the strides of the pooling operation.
Can be a single integer to specify the same value for
all spatial dimensions.
padding: A string. The padding method, either 'valid' or 'same'.
Case-insensitive.
data_format: A string. The ordering of the dimensions in the inputs.
`channels_last` (default) and `channels_first` are supported.
`channels_last` corresponds to inputs with shape
`(batch, height, width, channels)` while `channels_first` corresponds to
inputs with shape `(batch, channels, height, width)`.
name: A string, the name of the layer.
Returns:
Output tensor.
pooling层输入前后tensor的size计算方法如下:

8tf.contrib.layers.flatten()
flatten(*args, **kwargs)
Flattens the input while maintaining the batch_size.
Assumes that the first dimension represents the batch.
Args:
inputs: A tensor of size [batch_size, ...].
outputs_collections: Collection to add the outputs.
scope: Optional scope for name_scope.
Returns:
A flattened tensor with shape [batch_size, k].
Raises:
ValueError: If inputs rank is unknown or less than 2.
9tf.concat()
concat(values, axis, name='concat')
Concatenates tensors along one dimension.
Concatenates the list of tensors `values` along dimension `axis`. If
`values[i].shape = [D0, D1, ... Daxis(i), ...Dn]`, the concatenated
result has shape
[D0, D1, ... Raxis, ...Dn]
where
Raxis = sum(Daxis(i))
That is, the data from the input tensors is joined along the `axis`
dimension.
The number of dimensions of the input tensors must match, and all dimensions
except `axis` must be equal.
For example:
```python
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) ==> [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]]
# tensor t3 with shape [2, 3]
# tensor t4 with shape [2, 3]
tf.shape(tf.concat([t3, t4], 0)) ==> [4, 3]
tf.shape(tf.concat([t3, t4], 1)) ==> [2, 6]
```
Note: If you are concatenating along a new axis consider using stack.
E.g.
```python
tf.concat([tf.expand_dims(t, axis) for t in tensors], axis)
10 tf.nn.sparse_softmax_cross_entropy_with_logits()
sparse_softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, name=None)
Computes sparse softmax cross entropy between `logits` and `labels`.
Measures the probability error in discrete classification tasks in which the
classes are mutually exclusive (each entry is in exactly one class). For
example, each CIFAR-10 image is labeled with one and only one label: an image
can be a dog or a truck, but not both.
**NOTE:** For this operation, the probability of a given label is considered
exclusive. That is, soft classes are not allowed, and the `labels` vector
must provide a single specific index for the true class for each row of
`logits` (each minibatch entry). For soft softmax classification with
a probability distribution for each entry, see
`softmax_cross_entropy_with_logits`.
**WARNING:** This op expects unscaled logits, since it performs a `softmax`
on `logits` internally for efficiency. Do not call this op with the
output of `softmax`, as it will produce incorrect results.
A common use case is to have logits of shape `[batch_size, num_classes]` and
labels of shape `[batch_size]`. But higher dimensions are supported.
**Note that to avoid confusion, it is required to pass only named arguments to
this function.**
Args:
_sentinel: Used to prevent positional parameters. Internal, do not use.
labels: `Tensor` of shape `[d_0, d_1, ..., d_{r-1}]` (where `r` is rank of
`labels` and result) and dtype `int32` or `int64`. Each entry in `labels`
must be an index in `[0, num_classes)`. Other values will raise an
exception when this op is run on CPU, and return `NaN` for corresponding
loss and gradient rows on GPU.
logits: Unscaled log probabilities of shape
`[d_0, d_1, ..., d_{r-1}, num_classes]` and dtype `float32` or `float64`.
name: A name for the operation (optional).
Returns:
A `Tensor` of the same shape as `labels` and of the same type as `logits`
11 tf.Session().run()
The value returned by run() has the same shape as the fetches argument,
run(self, fetches, feed_dict=None, options=None, run_metadata=None)
method of tensorflow.python.client.session.Session instance
Runs operations and evaluates tensors in `fetches`.
This method runs one "step" of TensorFlow computation, by
running the necessary graph fragment to execute every `Operation`
and evaluate every `Tensor` in `fetches`, substituting the values in
`feed_dict` for the corresponding input values.
The `fetches` argument may be a single graph element, or an arbitrarily
nested list, tuple, namedtuple, dict, or OrderedDict containing graph
elements at its leaves. A graph element can be one of the following types:
* An @{tf.Operation}.
The corresponding fetched value will be `None`.
* A @{tf.Tensor}.
The corresponding fetched value will be a numpy ndarray containing the
value of that tensor.
* A @{tf.SparseTensor}.
The corresponding fetched value will be a
@{tf.SparseTensorValue}
containing the value of that sparse tensor.
* A `get_tensor_handle` op. The corresponding fetched value will be a
numpy ndarray containing the handle of that tensor.
* A `string` which is the name of a tensor or operation in the graph.
The value returned by `run()` has the same shape as the `fetches` argument,
where the leaves are replaced by the corresponding values returned by
TensorFlow.
Example:
```python
a = tf.constant([10, 20])
b = tf.constant([1.0, 2.0])
# 'fetches' can be a singleton
v = session.run(a)
# v is the numpy array [10, 20]
# 'fetches' can be a list.
v = session.run([a, b])
# v is a Python list with 2 numpy arrays: the 1-D array [10, 20] and the
# 1-D array [1.0, 2.0]
# 'fetches' can be arbitrary lists, tuples, namedtuple, dicts:
MyData = collections.namedtuple('MyData', ['a', 'b'])
v = session.run({'k1': MyData(a, b), 'k2': [b, a]})
# v is a dict with
# v['k1'] is a MyData namedtuple with 'a' (the numpy array [10, 20]) and
# 'b' (the numpy array [1.0, 2.0])
# v['k2'] is a list with the numpy array [1.0, 2.0] and the numpy array
# [10, 20].
```
The optional `feed_dict` argument allows the caller to override
the value of tensors in the graph. Each key in `feed_dict` can be
one of the following types:
* If the key is a @{tf.Tensor}, the
value may be a Python scalar, string, list, or numpy ndarray
that can be converted to the same `dtype` as that
tensor. Additionally, if the key is a
@{tf.placeholder}, the shape of
the value will be checked for compatibility with the placeholder.
* If the key is a
@{tf.SparseTensor},
the value should be a
@{tf.SparseTensorValue}.
* If the key is a nested tuple of `Tensor`s or `SparseTensor`s, the value
should be a nested tuple with the same structure that maps to their
corresponding values as above.
Each value in `feed_dict` must be convertible to a numpy array of the dtype
of the corresponding key.
The optional `options` argument expects a [`RunOptions`] proto. The options
allow controlling the behavior of this particular step (e.g. turning tracing
on).
The optional `run_metadata` argument expects a [`RunMetadata`] proto. When
appropriate, the non-Tensor output of this step will be collected there. For
example, when users turn on tracing in `options`, the profiled info will be
collected into this argument and passed back.
Args:
fetches: A single graph element, a list of graph elements,
or a dictionary whose values are graph elements or lists of graph
elements (described above).
feed_dict: A dictionary that maps graph elements to values
(described above).
options: A [`RunOptions`] protocol buffer
run_metadata: A [`RunMetadata`] protocol buffer
Returns:
Either a single value if `fetches` is a single graph element, or
a list of values if `fetches` is a list, or a dictionary with the
same keys as `fetches` if that is a dictionary (described above).
Raises:
RuntimeError: If this `Session` is in an invalid state (e.g. has been
closed).
TypeError: If `fetches` or `feed_dict` keys are of an inappropriate type.
ValueError: If `fetches` or `feed_dict` keys are invalid or refer to a
`Tensor` that doesn't exist.
12 tf.reduce_mean()
reduce_mean(input_tensor, axis=None, keep_dims=False, name=None, reduction_indices=None)
Computes the mean of elements across dimensions of a tensor.
Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keep_dims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keep_dims` is true, the reduced dimensions
are retained with length 1.
If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned.
For example:
```python
# 'x' is [[1., 1.]
# [2., 2.]]
tf.reduce_mean(x) ==> 1.5
tf.reduce_mean(x, 0) ==> [1.5, 1.5]
tf.reduce_mean(x, 1) ==> [1., 2.]
```
Args:
input_tensor: The tensor to reduce. Should have numeric type.
axis: The dimensions to reduce. If `None` (the default),
reduces all dimensions.
keep_dims: If true, retains reduced dimensions with length 1.
name: A name for the operation (optional).
reduction_indices: The old (deprecated) name for axis.
Returns:
The reduced tensor.
@compatibility(numpy)
Equivalent to np.mean
@end_compatibility
13 tf.cast()
cast(x, dtype, name=None)
Casts a tensor to a new type.
The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor`) to `dtype`.
For example:
```python
# tensor `a` is [1.8, 2.2], dtype=tf.float
tf.cast(a, tf.int32) ==> [1, 2] # dtype=tf.int32
```
Args:
x: A `Tensor` or `SparseTensor`.
dtype: The destination type.
name: A name for the operation (optional).
Returns:
A `Tensor` or `SparseTensor` with same shape as `x`.
Raises:
TypeError: If `x` cannot be cast to the `dtype`.
14 tf.train.AdamOptimizer()
class AdamOptimizer(tensorflow.python.training.optimizer.Optimizer)
| Optimizer that implements the Adam algorithm.
|
| See [Kingma et. al., 2014](http://arxiv.org/abs/1412.6980)
| ([pdf](http://arxiv.org/pdf/1412.6980.pdf)).
|
| Method resolution order:
| AdamOptimizer
| tensorflow.python.training.optimizer.Optimizer
| __builtin__.object
|
| Methods defined here:
|
| __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08, use_locking=False, name='Adam')
| Construct a new Adam optimizer.
|
| Initialization:
|
| ```
| m_0 <- 0 (Initialize initial 1st moment vector)
| v_0 <- 0 (Initialize initial 2nd moment vector)
| t <- 0 (Initialize timestep)
| ```
|
| The update rule for `variable` with gradient `g` uses an optimization
| described at the end of section2 of the paper:
|
| ```
| t <- t + 1
| lr_t <- learning_rate * sqrt(1 - beta2^t) / (1 - beta1^t)
|
| m_t <- beta1 * m_{t-1} + (1 - beta1) * g
| v_t <- beta2 * v_{t-1} + (1 - beta2) * g * g
| variable <- variable - lr_t * m_t / (sqrt(v_t) + epsilon)
| ```
|
| The default value of 1e-8 for epsilon might not be a good default in
| general. For example, when training an Inception network on ImageNet a
| current good choice is 1.0 or 0.1. Note that since AdamOptimizer uses the
| formulation just before Section 2.1 of the Kingma and Ba paper rather than
| the formulation in Algorithm 1, the "epsilon" referred to here is "epsilon
| hat" in the paper.
|
| The sparse implementation of this algorithm (used when the gradient is an
| IndexedSlices object, typically because of `tf.gather` or an embedding
| lookup in the forward pass) does apply momentum to variable slices even if
| they were not used in the forward pass (meaning they have a gradient equal
| to zero). Momentum decay (beta1) is also applied to the entire momentum
| accumulator. This means that the sparse behavior is equivalent to the dense
| behavior (in contrast to some momentum implementations which ignore momentum
| unless a variable slice was actually used).
|
| Args:
| learning_rate: A Tensor or a floating point value. The learning rate.
| beta1: A float value or a constant float tensor.
| The exponential decay rate for the 1st moment estimates.
| beta2: A float value or a constant float tensor.
| The exponential decay rate for the 2nd moment estimates.
| epsilon: A small constant for numerical stability. This epsilon is
| "epsilon hat" in the Kingma and Ba paper (in the formula just before
| Section 2.1), not the epsilon in Algorithm 1 of the paper.
| use_locking: If True use locks for update operations.
| name: Optional name for the operations created when applying gradients.
| Defaults to "Adam".
|
| ----------------------------------------------------------------------
| Methods inherited from tensorflow.python.training.optimizer.Optimizer:
apply_gradients(self, grads_and_vars, global_step=None, name=None)
| Apply gradients to variables.
|
| This is the second part of `minimize()`. It returns an `Operation` that
| applies gradients.
|
| Args:
| grads_and_vars: List of (gradient, variable) pairs as returned by
| `compute_gradients()`.
| global_step: Optional `Variable` to increment by one after the
| variables have been updated.
| name: Optional name for the returned operation. Default to the
| name passed to the `Optimizer` constructor.
|
| Returns:
| An `Operation` that applies the specified gradients. If `global_step`
| was not None, that operation also increments `global_step`.
|
| Raises:
| TypeError: If `grads_and_vars` is malformed.
| ValueError: If none of the variables have gradients.
|
| compute_gradients(self, loss, var_list=None, gate_gradients=1, aggregation_method=None, colocate_gradients_with_ops=False, grad_loss=None)
| Compute gradients of `loss` for the variables in `var_list`.
|
| This is the first part of `minimize()`. It returns a list
| of (gradient, variable) pairs where "gradient" is the gradient
| for "variable". Note that "gradient" can be a `Tensor`, an
| `IndexedSlices`, or `None` if there is no gradient for the
| given variable.
Args:
| loss: A Tensor containing the value to minimize.
| var_list: Optional list or tuple of `tf.Variable` to update to minimize
| `loss`. Defaults to the list of variables collected in the graph
| under the key `GraphKey.TRAINABLE_VARIABLES`.
| gate_gradients: How to gate the computation of gradients. Can be
| `GATE_NONE`, `GATE_OP`, or `GATE_GRAPH`.
| aggregation_method: Specifies the method used to combine gradient terms.
| Valid values are defined in the class `AggregationMethod`.
| colocate_gradients_with_ops: If True, try colocating gradients with
| the corresponding op.
| grad_loss: Optional. A `Tensor` holding the gradient computed for `loss`.
|
| Returns:
| A list of (gradient, variable) pairs. Variable is always present, but
| gradient can be `None`.
|
| Raises:
| TypeError: If `var_list` contains anything else than `Variable` objects.
| ValueError: If some arguments are invalid.
|
| get_name(self)
|
| get_slot(self, var, name)
| Return a slot named `name` created for `var` by the Optimizer.
|
| Some `Optimizer` subclasses use additional variables. For example
| `Momentum` and `Adagrad` use variables to accumulate updates. This method
| gives access to these `Variable` objects if for some reason you need them.
|
| Use `get_slot_names()` to get the list of slot names created by the
| `Optimizer`.
| Args:
| var: A variable passed to `minimize()` or `apply_gradients()`.
| name: A string.
|
| Returns:
| The `Variable` for the slot if it was created, `None` otherwise.
|
| get_slot_names(self)
| Return a list of the names of slots created by the `Optimizer`.
|
| See `get_slot()`.
|
| Returns:
| A list of strings.
|
| minimize(self, loss, global_step=None, var_list=None, gate_gradients=1, aggregation_method=None, colocate_gradients_with_ops=False, name=None, grad_loss=None)
| Add operations to minimize `loss` by updating `var_list`.
|
| This method simply combines calls `compute_gradients()` and
| `apply_gradients()`. If you want to process the gradient before applying
| them call `compute_gradients()` and `apply_gradients()` explicitly instead
| of using this function.
|
| Args:
| loss: A `Tensor` containing the value to minimize.
| global_step: Optional `Variable` to increment by one after the
| variables have been updated.
| var_list: Optional list or tuple of `Variable` objects to update to
| minimize `loss`. Defaults to the list of variables collected in
| the graph under the key `GraphKeys.TRAINABLE_VARIABLES`.
| gate_gradients: How to gate the computation of gradients. Can be
| `GATE_NONE`, `GATE_OP`, or `GATE_GRAPH`.
| aggregation_method: Specifies the method used to combine gradient terms.
| Valid values are defined in the class `AggregationMethod`.
colocate_gradients_with_ops: If True, try colocating gradients with
| the corresponding op.
| name: Optional name for the returned operation.
| grad_loss: Optional. A `Tensor` holding the gradient computed for `loss`.
|
| Returns:
| An Operation that updates the variables in `var_list`. If `global_step`
| was not `None`, that operation also increments `global_step`.
|
| Raises:
| ValueError: If some of the variables are not `Variable` objects.
|
| ----------------------------------------------------------------------
| Data descriptors inherited from tensorflow.python.training.optimizer.Optimizer:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
|
| ----------------------------------------------------------------------
| Data and other attributes inherited from tensorflow.python.training.optimizer.Optimizer:
|
| GATE_GRAPH = 2
|
| GATE_NONE = 0
|
| GATE_OP = 1
15.tensorflow.contrib.slim.python.slim.nets
NAME
tensorflow.contrib.slim.python.slim.nets
PACKAGE CONTENTS
alexnet
inception
inception_v1
inception_v2
inception_v3
overfeat
resnet_utils
resnet_v1
resnet_v2
vgg
16.tensorflow.contrib.slim.python.slim.nets.resnet_v1
NAME
tensorflow.contrib.slim.python.slim.nets.resnet_v1 - Contains definitions for the original form of Residual Networks.
DESCRIPTION
The 'v1' residual networks (ResNets) implemented in this module were proposed
by:
[1] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Deep Residual Learning for Image Recognition. arXiv:1512.03385
Other variants were introduced in:
[2] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Identity Mappings in Deep Residual Networks. arXiv: 1603.05027
The networks defined in this module utilize the bottleneck building block of
[1] with projection shortcuts only for increasing depths. They employ batch
normalization *after* every weight layer. This is the architecture used by
MSRA in the Imagenet and MSCOCO 2016 competition models ResNet-101 and
ResNet-152. See [2; Fig. 1a] for a comparison between the current 'v1'
architecture and the alternative 'v2' architecture of [2] which uses batch
normalization *before* every weight layer in the so-called full pre-activation
units.
Typical use:
from tensorflow.contrib.slim.python.slim.nets import
resnet_v1
ResNet-101 for image classification into 1000 classes:17.tensorflow.contrib.slim.python.slim.nets.resnet_v1 .resnet_v1_block()
Help on function resnet_v1_block in module tensorflow.contrib.slim.python.slim.nets.resnet_v1:
resnet_v1_block(scope, base_depth, num_units, stride)
Helper function for creating a resnet_v1 bottleneck block.
Args:
scope: The scope of the block.
base_depth: The depth of the bottleneck layer for each unit.
num_units: The number of units in the block.
stride: The stride of the block, implemented as a stride in the last unit.
All other units have stride=1.
Returns:
A resnet_v1 bottleneck block.
18.tensorflow.contrib.slim.python.slim.nets.resnet_utils
NAME
tensorflow.contrib.slim.python.slim.nets.resnet_utils - Contains building blocks for various versions of Residual Networks.
DESCRIPTION
Residual networks (ResNets) were proposed in:
Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Deep Residual Learning for Image Recognition. arXiv:1512.03385, 2015
More variants were introduced in:
Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Identity Mappings in Deep Residual Networks. arXiv: 1603.05027, 2016
We can obtain different ResNet variants by changing the network depth, width,
and form of residual unit. This module implements the infrastructure for
building them. Concrete ResNet units and full ResNet networks are implemented in
the accompanying resnet_v1.py and resnet_v2.py modules.
Compared to https://github.com/KaimingHe/deep-residual-networks, in the current
implementation we subsample the output activations in the last residual unit of
each block, instead of subsampling the input activations in the first residual
unit of each block. The two implementations give identical results but our
implementation is more memory efficient.
CLASSES
Block(builtins.tuple)
Block
class Block(Block)
19.tf.py_func(func, inp, Tout, stateful=True, name=None)
Wraps a python function and uses it as a TensorFlow op.
Given a python function `func`, which takes numpy arrays as its
inputs and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
```python
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
inp = tf.placeholder(tf.float32)
y = tf.py_func(my_func, [inp], tf.float32)
```
**N.B.** The `tf.py_func()` operation has the following known limitations:
* The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment.
* The operation must run in the same address space as the Python program
that calls `tf.py_func()`. If you are using distributed TensorFlow, you
must run a `tf.train.Server` in the same process as the program that calls
`tf.py_func()` and you must pin the created operation to a device in that
server (e.g. using `with tf.device():`).
实例
#encoding:utf-8
'''
通过tf.py_func(func, inp, Tout, stateful=True, name=None)可以将任意的python函数func
转变为TensorFlow op。func接收的输入必须是numpy array,可以接受多个输入参数;
输出也是numpy array,也可以有多个输出。inp传入输入值,Tout指定输出的基本数据类型
'''
import numpy as np
import tensorflow as tf
array1 = np.array([[1, 2], [3, 4]], dtype=np.float32)
array2 = np.array([[5, 6], [7, 8]], dtype=np.float32)
def add_minus_dot(array1, array2):
return array1 + array2, array1 - array2, np.dot(array1, array2)
sess = tf.Session()
add_minus_dot_op = tf.py_func(add_minus_dot, [array1, array2], [tf.float32, tf.float32, tf.float32])
print( sess.run(add_minus_dot_op))