PLA算法的理解（perceptron learning algorithm）

最近在学习台大林轩田教授的课程，一开始就讲到了perceptron learning algorithm，这个算法是用来对线性可分数据进行分类的。要注意这里是线性可分的数据，这个也是PLA算法的局限的地方，如果PLA算法运用在线性不可分的数据中的时候，算法将会无限循环下去，还有就是即使我们的数据是线性可分的，我们也不知道PLA算法什么时候才能找到一个最优的解，可能循环操作几次就可以得到，也有可能需要很多次才能找到最优解，其实在不知道的情况下，我们无法预计算法需要计算多久，这样其实是开销很大的，后续我们基于贪心算法（greedy algorithm）对PLA算法进行了改进，我们每一次的计算都保留当前的最优解，意思就是找到一个相对最优解，然后我们不断去更新优化这个最优解。
首先我们PLA算法是用来求解分类的那条分界线的，也就是求解我们$W\text{ = { }{\text{w}}_1\text{,}{\text{w}}_2\text{,}...\text{,}{\text{w}}_n\text{} }$向量，假设我们的数据集为$X\text{ = { }{\text{x}}_1\text{,}{\text{x}}_2\text{,}...\text{,}{\text{x}}_n\text{} }$，我们可以用这条线将我们的数据X分成正负两个部分，用数学表达式可以将假设函数h(x)表示成：
$$h(x)=sign(\sum _{i=1}^n{w}_i{x}_i-threshold)$$
我们将分界线的向量和数据集进行内积运算，然后减去一个阈值，最后加上一个sign函数将数据进行分类操作，结果1表示正类，-1表示负类。在这个公式里这个阈值看着比较碍眼，我们可以将阈值项threshold看作是w0和x0相乘，w0看做是-threshold，x0看做是1，那么整个公式可以表示成：
$$\begin{gathered} h(x)=sign(\sum _{i=1}^n{w}_i{x}_n-threshold)=sign(\sum _{i=1}^n{w}_i{x}_n+(-threshold)(+1)) \\ =sign(\sum _{i=1}^n{w}_i{x}_i+w_0{x}_0)=sign(\sum _{i=0}^n{w}_i{x}_i)=sign(W^{T}X) \end{gathered}$$
由上述数学公式我们可以得到$h(x)=sign(W^{T}X)$，在假设函数h(x)中，X是已知的数据集，要求W的向量，$W^{T}X$的值会把我们数据集分成正负两个类，PLA的算法就是在不断地纠正我们的分类错误，纠正的方法如下所示：

1. 正类+1被预测到了负类-1
   这个时候，x的实际指向是正方向，也就是说y=+1，但是预测到了-1，也就是说$W^{T}X=-1$，这里x的指向表示y的布尔值，我们可以用向量图来表示：
   
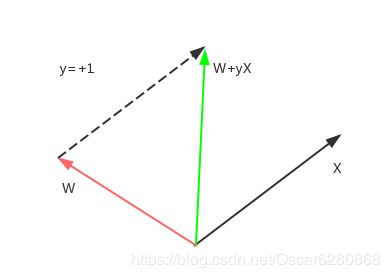
   在上图中X是正类，但是与预测的W向量夹角大于90度，所以$W^{T}X=-1$，我们如何来纠正这个向量呢？我们可以将W和X向量相加，这里需要注意的是X还需要乘以一个y，来表示向量的方向，同时也表示W分割线调整的方向。这个时候y=+1，所以我们新调整的W是W+X，如图所示，红色的向量表示预测错误的向量，我们加上实际的X向量，就可以得到调整之后的绿色的向量，可以看到绿色的向量相比红色的向量更加靠近X向量了，夹角也小于90度，这样就可以纠正原来的错误预测了。
2. 负类-1被预测到了正类+1
   同样的道理，X的向量指向负的情况下，但是由于预测错误，W向量和X向量夹角小于90度，所以$W^{T}X=1$，我们同样需要y*X来调整新的预测，我们可以得到下图：
   
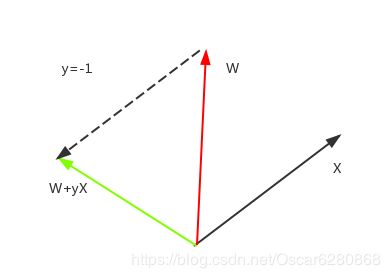
   由上图可以看出，黑色的向量X和红色的向量W，由于夹角小于90度，所以$W^{T}X=1$，这个时候需要调整新的W向量，这个时候y=-1，所以W+yX=W-X，就相当于是两个向量相减，得到新的调整之后的绿色的向量，这样新调整的向量与原有的X向量的夹角大于90度，那么$W^{T}X=-1$，这样错误就纠正了。

有了上面就正错误点的方法，我们可以不断地更新W，直到找到最优解，用伪代码可以表示成：

init w(0)=0
for t = 0,1,2,3,...:
	for i = 1,2,3,4,...,n:
		w(t+1) = w(t) + y(i) * x(i)
end
//直到所有的点都被正确分类，我们就停止更新W

有的朋友就会有疑问了，会不会有这个循环停不下来的情况，答案是不会的，这个算法到最后一定是会停下来的。下面我们就来证明一下。首先我们假设有一条理想的分割线$W_f$，因为$y_n$和$W_f^T{X}_n$一定是同号的，那么$y_n{W}_f^T{X}_n$一定是大于0的，所以可以得到：
$$y_{n(t)}{W}_f^T{X}_{n(t)}⩾\underset{n}{\min }{y}_n{W}_f^T{X}_n>0$$
我们再来看看理想分割线和我们预测的分割线的内积：
$$W_f^T{W}_{t+1}=W_f^T(W_t+y_{n(t)}{X}_{n(t)})⩾W_f^T{W}_t+\underset{n}{\min }{y}_n{W}_f^T{X}_n>W_f^T{W}_t+0=W_f^T{W}_t$$
由上述式子是可以得到$W_f^T{W}_t$随着t的增加是递增的，所以说每一次的纠正错误，我们预测的$W_t$与理想的分割线$W_f$越来越接近，但是也有可能是两个向量的夹角在减小，也有可能是调整的向量在增大，所以我们还需要确定是哪一种情况，我们再来看看下面的推导：
$$\begin{gathered} {\Vert W_{t+1}\Vert }^2={\Vert W_t+y_{n(t)}{X}_{n(t)}\Vert }^2={\Vert W_t\Vert }^2+2y_{n(t)}{W}_t^T{X}_{n(t)}+{\Vert y_{n(t)}{X}_{n(t)}\Vert }^2 \\ ⩽{\Vert W_t\Vert }^2+0+{\Vert y_{n(t)}{X}_{n(t)}\Vert }^2⩽{\Vert W_t\Vert }^2+\underset{n}{\max }{\Vert y_n{X}_n\Vert }^2 \end{gathered}$$
由上述的数学公式我们可以得到${\Vert W_{t+1}\Vert }^2⩽{\Vert W_t\Vert }^2+\underset{n}{\max }{\Vert y_n{X}_n\Vert }^2$，可以看出虽然每次更新的分割线向量长度都在递增，但是每次递增都是受限制的，所以综上我们可以得到，PLA算法到最后一定是会停止的，但是要多久会停下来呢，我们再来证明：
$$W_f^T{W}_t=W_f^T(W_{t-1}+y_{n(t-1)}{X}_{n(t-1)})⩾W_f^T{W}_{t-1}+\underset{n}{\min }{y}_n{W}_f^T{X}_n$$
我们可以将T次调整更新的结果进行叠加，就可以得到：
$$W_f^T{W}_t⩾W_0+T\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n$$
因为在初始化的时候$W_0$=0，所以$W_f^T{W}_t⩾T\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n$，在上述数学公式中我们就可以推导出：
$${\Vert W_t\Vert }^2⩽{\Vert W_{t-1}\Vert }^2+{\Vert y_{n(t-1)}{X}_{n(t-1)}\Vert }^2⩽{\Vert W_{t-1}\Vert }^2+\underset{n}{\max }{\Vert X_n\Vert }^2⩽\Vert W_0\Vert +T\cdot \underset{n}{\max }{\Vert X_n\Vert }^2$$
因为初始化$W_0$=0，所以可以得到${\Vert W_t\Vert }^2⩽T\cdot \underset{n}{\max }{\Vert X_n\Vert }^2$，由上述的推论我们最终可以得到如下的推论：
$$\begin{gathered} \frac{W_f^T}{\Vert W_f\Vert }\frac{W_T}{\Vert W_T\Vert }=\frac{T\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n}{\Vert W_f^T\Vert \Vert W_t\Vert }⩾\frac{T\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n}{\Vert W_f^T\Vert \cdot \sqrt{T}\cdot \underset{n}{\max \Vert X_n\Vert }} \\ ⩾\frac{\sqrt{T}\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n}{\Vert W_f^T\Vert \cdot \underset{n}{\max \Vert X_n\Vert }}=\sqrt{T}\cdot constant \end{gathered}$$
因为$\frac{W_f^T}{\Vert W_f\Vert }\frac{W_T}{\Vert W_T\Vert }=\cos \theta ⩽1$，所以我们可以推导出$\frac{\sqrt{T}\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n}{\Vert W_f^T\Vert \cdot \underset{n}{\max \Vert X_n\Vert }}⩽1$，这时候我们来定义一下：$R^2=\underset{n}{\max }{\Vert X_n\Vert }^2$，$\rho =\underset{n}{\min }{y}_n\frac{W_f^T}{\Vert W_f\Vert }{X}_n$，这时候我们可以得到最终的推论：
$$\begin{gathered} \frac{\sqrt{T}\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n}{\Vert W_f^T\Vert \cdot \underset{n}{\max \Vert X_n\Vert }}⩽1\iff \sqrt{T}\cdot \underset{n}{\min }{y}_n{W}_f^T{X}_n⩽\Vert W_f^T\Vert \cdot \underset{n}{\max }\Vert X_n\Vert \\ \iff \sqrt{T}⩽\frac{\Vert W_f^T\Vert \cdot \underset{n}{\max \Vert X_n\Vert }}{\underset{n}{\min }{y}_n{W}_f^T{X}_n}=\frac{R}{\rho }\iff T⩽\frac{R^2}{{\rho }^2} \end{gathered}$$
所以综上所述，我们纠正迭代的次数T是有上界的，所以说只要数据是线性可分的，那么通过有限次的更新纠正，我们一定可以通过PLA算法找一条分割线来分割我们的数据集。
希望这篇博文能给大家在PLA算法的理解上有所帮助，文中如有疑问或纰漏之处，也望各位朋友批评指正，如有转载，也请标明文章的出处，蟹蟹。