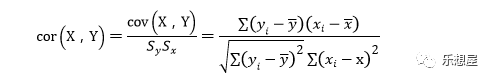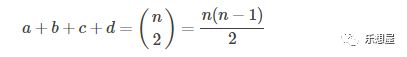聚类分析理论介绍
1、聚类分析概述及基本思想
聚类分析(cluster analysis)也称群分析、点群分析,是一种无监督学习,与回归分析、多元分析称为多元分析的三大方法。是一个把数据对象划分成子集的过程。每个子集是一个簇(cluster),使得簇中的对象彼此相似,但是与其他簇中的对象不相似。由聚类分析产生的一个簇的集合叫做一个聚类。例如,可以根据各个银行网点的储蓄量、人力资源状况、营业面积、特色功能、网点级别、所处功能区域等因素情况,将网点分为几个等级,再比较各银行之间不同等级网点数量对比状况。
基本思想:
我们所研究的样品或指标(变量)之间存在程度不同的相似性(亲疏关系——以样品间距离衡量)。于是根据一批样品的多个观测指标,具体找出一些能够度量样品或指标之间相似程度的统计量,以这些统计量为划分类型的依据。把一些相似程度较大的样品(或指标)聚合为一类,把另外一些彼此之间相似程度较大的样品(或指标)又聚合为另一类,直到把所有的样品(或指标)聚合完毕,满足“类内差异小,类间差异大”,这就是分类的基本思想。也就是“物以类聚”的思想。
聚类分析的特征:
分组:聚类分析的过程就是把一个数据对象分成若干个组(或者簇)的过程。
相似:组内的对象具有很高的相似性,而对于另外一些组,则要求尽可能的不相似。
评估:聚类完成后,还需要一些评价函数对聚类结果进行度量,通常涉及距离度量。
2、聚类算法的分类:
聚类分析根据分类对象的不同,可分为:
1)对指标变量进行分类称为R型聚类分析
思想:通过对变量的相关系数矩阵内部结构的研究,找出能够控制所有变量的少数几个随机变量去描述多个随机变量之间的相关关系。然后再根据相关性的大小把变量分组,使同组内的变量之间的相关性较高,不同组变量之间的相关性较低。
优点:a)不但可以了解个别变量之间的关系的亲疏程度,而且可以了解各个变量组合之间的亲疏程度。b)根据变量的分类结果以及它们之间的关系,可以选择主要变量进行回归分析或Q型聚类分析。
2)对样本进行分类称为Q型聚类分析。
-
它的思路与R因子分析相同,只是出发点不同而已。它在计算中是从样品的相似系数矩阵出发,而R型因子分析在计算中是从样品的相关系数矩阵出发的。
优点:a)可以综合利用多个变量的信息对样本进行分类;b)分类结果是直观的,聚类谱系图非常清楚地表现其数值分类结果;c)聚类分析所得到的结果比传统分类方法更细致、全面、合理。
3、聚类分析的步骤
步骤1:选择聚类分析变量;
这些变量应具备以下特点:1)和聚类分析的目标相关;2)反映了要分类对象的特征;3)在不同对象的值具有明显差异;4)变量之间不应该高度相关
对于变量高度相关的处理办法(两种):
1)在对案例聚类分析之前,先对变量进行聚类分析,在各类中选择具有代表性的变量作为聚类变量;
2)对变量做因素分析,产生一组不相关变量作为聚类变量。
步骤2:计算相似性
相似性(Similarity)是聚类分析的一个基本概念,反映了研究对象之间的亲疏程度。聚类分析就是根据研究对象之间的相似性来进行分类的。
步骤3:聚类
选定聚类方法,确定形成的类数。
步骤4:聚类结果的解释
得到聚类结果后,对结果进行验证和解释,以保证聚类解是可信的。
4、聚类算法中相似性度量(Similarity Measurement):
事物相似性的度量标准一般有两种:距离和相似性系数,距离一般用来度量样本之问的相似性;而相似性系数,一般用来度量变量之间的相似性。
采用什么样的方法计算距离是很讲究,甚至关系到分类的正确与否。 首先我们需要定义样品间的距离,每个样品有p个指标(变量),故每个样品可以看成p维空间中的一个点,n个样品组成p维空间中的n个点,用距离来度量样品之间接近的程度。距离测度应满足下列四个条件:
1)dij³0;
2)dij=dji, 即距离具有对称性;
3)dij£dik+dkj,即三角不等式,任意一边小于其他两边之和;
4)如果dij¹0,则i ¹j
常见的距离 :
曼哈顿(绝对值)距离、欧氏距离、切比雪夫距离、闵可夫斯基距离、马氏距离、兰氏距离等
4-1 曼哈顿距离或绝对值距离|
4-2 欧式距离
欧氏距离有明显的缺点:它将样品的不同属性(即各指标或各变量)之间的差别等同看待;如下图:除了绿线为欧式距离,其他均为曼哈顿距离
4-3切比雪夫距离
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
4-4 闵可夫斯基距离
闵氏距离的缺点:
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
将各个分量的量纲(scale),也就是“单位”当作相同的看待了。
没有考虑各个分量的分布(期望,方差等)可能是不同的。
例如案例:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?
因此,当各指标的测量值相差悬殊时,先对数据标准化,然后,用标准化后的数据计算距离
4-5 马氏距离
马氏距离表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法;与欧氏距离不同的是,它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。
马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰。
在计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在。
4-6 兰氏距离
兰氏距离是一个无量纲的指标,克服了闵可夫斯基距离与各指标的量纲有关的缺点,且兰氏距离对大的奇异值不敏感,这使其特别适合高度偏移的和数据。但兰氏距离也没有考虑变量间的相关性。
闵可夫斯基距离和兰氏距离都是假定变量之间相互独立,即在正交空间中讨论距离。但在实际问题中,变量之间往往存在着一定的相关性,为克服变量之间相关性的影响,可以采用马氏距离。
相似性系数度量:夹角余弦、相关系数
4-7 夹角余弦
余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1,接近于0,表示两个向量近乎于正交。
4-8 相关系数
可以看出:
相关系数具有对称性cor(y,x)=cor(x,y)
相关系数不再受量纲的影响,范围满足-1<=cor(y,x)<=1,其绝对值越靠近1,线性相关性越强。
相关系数的符号反映了y和x关系的方向。当cor(y,x)>0时,y和x正相关,当cor(y,x)<0时,y和x负相关。
相关系数只是刻画线性关系的大小,当cor(y,x)=0时,并不说明没有相关性,只是y和x不存在线性相关性,但有可能存在非线性关系。
参考文件:http://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
5、聚类算法:
根据原理不同,可分为
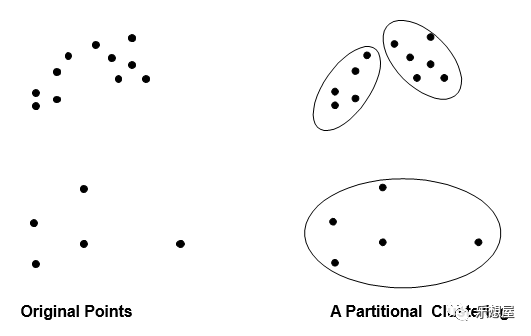
划分聚类法(Partitional Clustering):是聚类分析最简单最基本的方法,采取互斥簇的划分,即每个对象必须恰好属于一个组。划分方法是基于距离的,给定要构建的分区数k,划分方法首先创建一个初始划分,然后它采用一种迭代的重定位技术,通过把对象从一个组移动到另一个组来改进划分。一个好的划分准则是:同一个簇中的相关对象尽可能相互“接近”或相关,而不同簇中的对象尽可能地“远离”或不同。如k-均值(k-means)和k-中心点(k-mediods)方法。
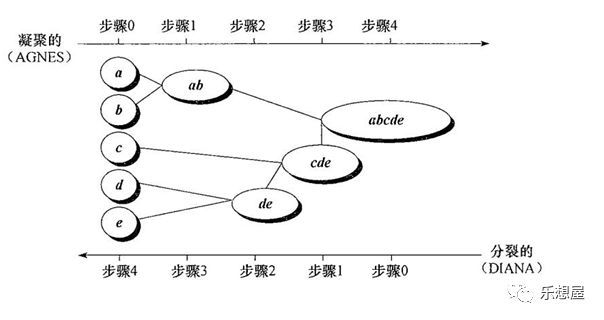
层次聚类(Hierarchical Clustering)。层次方法创建给定数据对象集的层次分解。层次方法可以分为凝聚和分裂的方法。凝聚的方法,也称自底向上的方法,开始将每个对象作为单独的一组,然后逐次合并相近的对象或组,直到所有的组合并成为一个组。分裂的方法,也成为自顶向下的方法,开始将所有的对象置于一个簇中,在每次的迭代中,一个簇被划分为更小的簇,直到每个最终每个对象在单独的一个簇中。
基于密度的聚类。大部分划分方法基于对象之间的距离进行聚类,这样的方法只能发现球状簇,而在发现任意形状簇时遇到了困难。基于密度的聚类方法主要思想是:只要“邻域”中的密度(对象或数据点的数目)超过了某个阈值(用户自定义),就继续增长给定的簇。基本的思想是通过是否紧密相连来判断样本点是否属于一个簇。代表性的算法就是DBSCAN。
基于网络的方法。把对象空间量化为有限个单元,形成一个网格结构。所有的聚类操作都在这个网格上进行。这种方法的主要优点是处理速度快。
基于模型的方法。神经网络聚类算法之SOM,以及模糊聚类的FCM算法。
详细的聚类算法介绍:
5-1 划分聚类法中的k-means算法。
k-means应该是聚类算法中最为基础但也最为重要的算法,以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。
k-means算法的处理过程如下:
随机地选择k个对象,每个对象初始地代表了一个簇的平均值或中心;
对剩余的每个对象,根据其与各簇中心的距离,将它赋给最近的簇;
如果某个点 p 离第 n 个质心的距离更近,则该点属于簇n,并对其打标签,标注 point p.label=n,其中 n<=k;
重新计算每个簇的平均值;
迭代至所有簇的平均值都不变化为止,即算法结束。
当然算法实现的方法有很多,比如在选择初始质心时,可以随机选择 k 个,也可以随机选择 k 个离得最远的点等等,方法不尽相同。
K均值的优缺点:
优点:简单,易于理解和实现。时间复杂度低。
缺点:
要手工输入K值,对初始值的设置很敏感。也是k均值最大的问题。
对噪声和离群点很敏感。
只用于数值型数据,不适用于分类类型的数据。
不能解决非凸数据。
主要发现圆形或者球形簇,不能识别非球形的簇。
k均值常用的邻近度,质心和目标函数的选择:
邻近度函数:曼哈顿距离。质心:中位数。目标函数:最小化对象到其簇质心的距离和。
邻近度函数:平方欧几里德距离。质心:均值。目标函数:最小化对象到其簇质心的距离的平方和。
邻近度函数:余弦。质心:均值。最大化对象与其质心的余弦相似度和。
邻近度函数:Bregman散度。质心:均值。目标函数:最小化对象到其簇质心的Bregman散度和。
5-2 层次聚类法中的凝聚层次聚类
有两种产生层次聚类的基本方法:
凝聚的。从点作为个体簇开始,每一步合并两个最接近的簇。这需要定义簇的临近性概念。凝聚层次聚类技术是最常见的。
分裂的。从包含所有点的某个簇开始,每一步分裂一个簇,直到仅剩下单点簇。在这种情况下,我们需要确定每一步分裂哪个簇,以及如何分裂。
基本凝聚层次聚类算法的过程:
如果需要,计算临近度矩阵
重复步骤
合并最接近的两个簇,簇与簇合并的原则永远是距离最小
更新临近度矩阵,以反映新的簇与原来的簇之间的临近性。
直到仅剩下一个簇
计算距离值,可以采用MIN、MAX、GROUP、AVG 3种方式:
MIN(单链)。不同簇中的两个最近的点之间的距离作为临近度。
MAX(全链)。不同簇中的两个最远的点之间的距离作为临近度。
GROUP(组平均)。取自不同簇的所有点对距离的平均值作为临近度。
5-3 基于密度的DBSCAN方法:
密度聚类的思想是不同于KMeans的,但是更符合我们人类的思维,基本的思想是通过是否紧密相连来判断样本点是否属于一个簇。代表性的算法就是DBSCAN,它基于一组邻域参数(ϵ,MinPts)(ϵ,MinPts)来表征某处样本是否是紧密的。用户先指定一个参数ϵ>0用来指定每个对象的邻域半径。对象o的ϵ-邻域是以o为中心、以ϵ为半径的空间。它是一种基于高密度连通区域的、基于密度的聚类算法,能够将具有足够高密度的区域划分为簇,并在具有噪声的数据中发现任意形状的簇。
DBSCAN算法需要输入2个参数:
一个参数是半径(Eps),表示以给定点P为中心的圆形邻域的范围;
另一个参数是以点P为中心的邻域内最少点的数量(MinPts)。如果满足:以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts,则称点P为核心点。
如果想找离群点就设置小一些半径,或者最小的数据量,最小的数量可以使用4尝试。
DBSCAN算法流程:
首先标记所有的对象为“未探索”
然后随机选择一个为探索的对象p并标记为“已探索”
如果p的e-邻域至少有MinPts(邻域密度阈值)个对象,则创建一个新的簇C,并把p添加到C中,并把它们记作N,遍历N中的每个成员p',如果p'的邻域也至少有MinPts个对象则保留,否则把p'从N中删除。
否则标记p为噪声
直到把所有的对象都遍历完为止。
DBSCAN的优点:
不需要指定簇的个数
可以解决数据分布特殊(非凸, 互相包络,长条形等)的情况
对于噪声不敏感
速度较快,可适用于较大的数据集
在邻域参数(ϵ,MinPts)(ϵ,MinPts)给定的情况下,结果是确定的,只要数据进入算法的顺序不变,与初始值无关,这里就和KMeans不同
缺点:
簇之间密度差距过大时效果不好,因为对整个数据集我们使用的是一组邻域参数
数据集较大的时候很消耗内存,目前在scikit-learn中已经可以使用ball-trees 和 kd-trees来确定邻居点(可以看出找出点的邻域内有几个点是DBSCAN最基本,最多的操作),但是在默认情况下是不使用他们的,而是使用很消耗内存的距离矩阵。
对于高维数据距离的计算会比较麻烦,造成"维数灾难"
参考文章:https://blog.csdn.net/leonliu1995/article/details/78944798
6、聚类评估
聚类评估估计在数据集上进行聚类的可行性和被聚类方法产生的结果的质量。聚类评估主要包括:估计聚类趋势、确定数据集中的簇数、测定聚类质量。
6-1 估计聚类趋势
聚类趋势评估确定给定的数据集是否具有可以导致有意义的聚类的非随机结构。一个没有任何非随机结构的数据集,如数据空间中均匀分布的点,尽管聚类算法可以为该数据集返回簇,但这些簇是随机的,没有任何意义.。
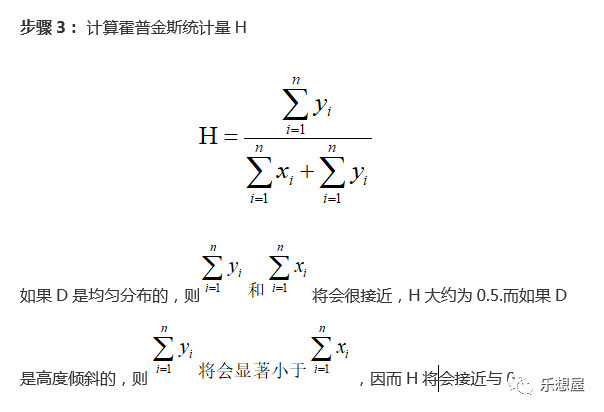
霍普金斯统计量(Hopkins Statistic)是一种空间统计量,检验空间分布的变量的空间随机性。可以用于评估数据集被均匀分布的概率;
给定数据集D,它可以看作是随机变量o的一个样本,我们想要确定o在多大程度上不同于数据空间中的均匀分布。可以按照以下步骤计算霍金斯统计量:
6-2 确定数据集中的簇数
确定数据集中“正确的”簇数是重要的,不仅因为像k-均值这样的聚类算法需要这种参数,而且因为合适的簇数可以控制适当的聚类分析粒度。这可以看做在聚类分析的可压缩性与准确性之间寻找好的平衡点。
6-3 测定聚类质量
在数据集上使用聚类方法之后,需要评估结果簇的质量。评价标准是:聚类结果“簇内相似度”(intra-cluster similarity)高,而“簇间相似度”(inter-cluster similarity)低。主要分为两类:
外部评估(external evaluation):将结果与某个“参考模型”(reference model)进行比较;又称为无监督方法。
内部评估(internal evaluation):直接考虑聚类结果而不利用任何参考模型。又称监督方法。
如果有可用的基准,则外部评估方法可以使用它。外部评估方法比较聚类结果和基准。如果没有基准可用,则可以使用内在评估方法。
1、外部评估
那么所有配对的总数为:
通常基准是一种理想的聚类,通常由专家构建。
质量度量Q:
簇的同质性:簇内越纯越好,聚类越好。
簇的完整性:能够将基准数据中属于相同类的样本聚类为相同的类
碎布袋:在多种实际情况下,常常有一种“碎布袋”类别,包含一些不能与其他对象合并的对象。这种类别通常称为“杂项”、“其他”等。碎布袋准则是说,把一个异种数据加入纯类应该比放入碎布袋受到更大的“处罚”。
小簇的保持性:如果小的类别在聚类中被划分为小片,则这些小片很可能称为噪声,从而小的类别就不可能被该聚类发现。小簇保持准则是说,把小簇划分成更小簇比把大簇划分为小簇的危害更大
BCubed精度和召回率:
一个对象的精度指示同一个簇中有多少个其他对象与该对象同属一个类别。
一个对象的召回率反映有多少同一类别的对象被分配在相同的簇中。
2、内部评估
内在方法通过考察簇的分离情况和簇的紧凑情况来评估聚类。许多内在方法都利用数据集的对象之间的相似性度量。比如,轮廓系数(silhouette coefficient)。
轮廓系数(silhouette coefficient)
轮廓系数的值在-1和1之间。a(o)的值反映o所属的簇的紧凑性。该值越小,簇越紧凑。b(o)的值捕获o与其他簇的分离程度。b(o)的值越大,o与其他簇越分离。当o的轮廓系数值接近1时,包含o的簇是紧凑的,并且o远离其他簇,这是一种可取的情况。当轮廓系数的值为负时,这意味在期望情况下,o距离其他簇的对象比距离与自己同在簇的对象更近,许多情况下,这很糟糕,应当避免。
参考文章
https://blog.csdn.net/love__live1/article/details/83960281
https://blog.csdn.net/u011511601/article/details/82195129