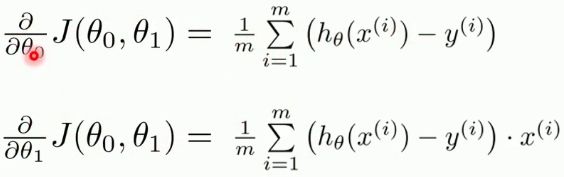2.一元线性回归（代价函数和梯度下降法）

概念：回归分析（Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。其中，被用来预测的变量叫做自变量，被预测的变量叫做因变量。如果包含两个以上的自变量，则称为多元回归分析。

比方说有一个公司，每月的广告费用和销售额，如下表所示：

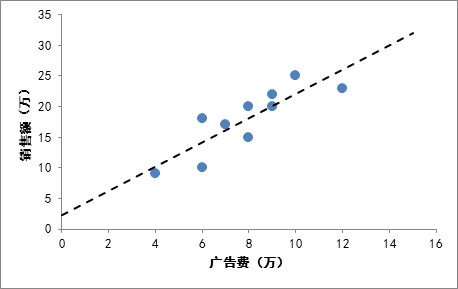
如果我们把广告费和销售额画在二维坐标内，就能够得到一个散点图，如果想探索广告费和销售额的关系，就可以利用一元线性回归做出一条拟合直线：

拟合直线

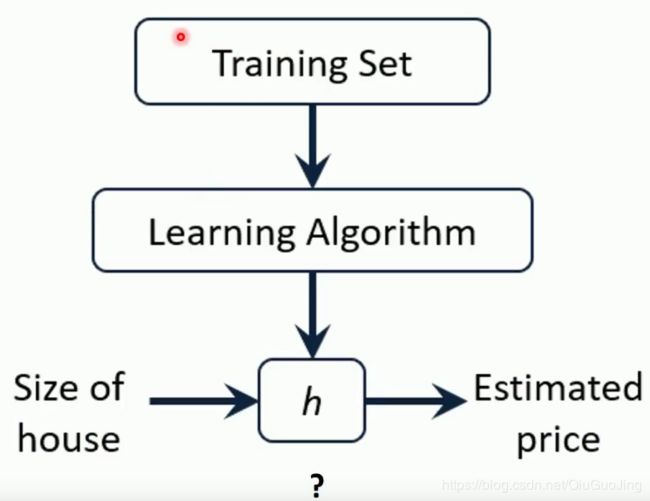
建模的流程：

一元线性回归的数学表达式：

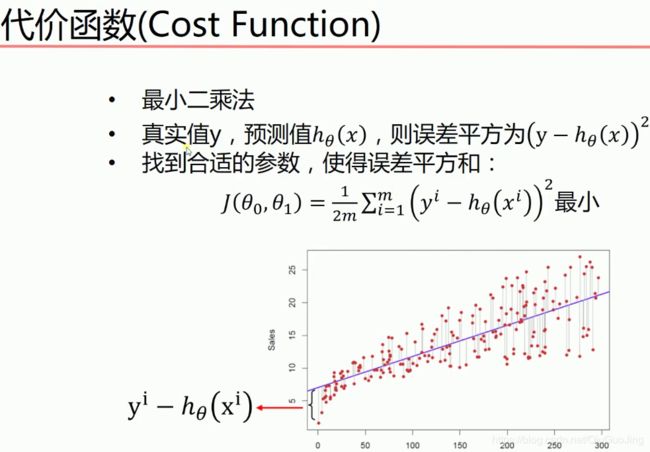
那么，这条直线该怎么画出来呢？这个就牵扯到代价函数和梯度下降法了！

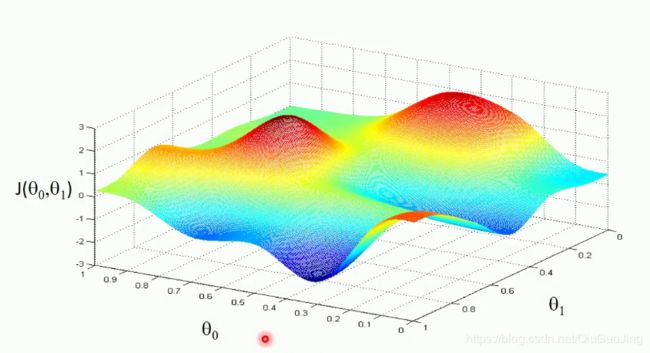
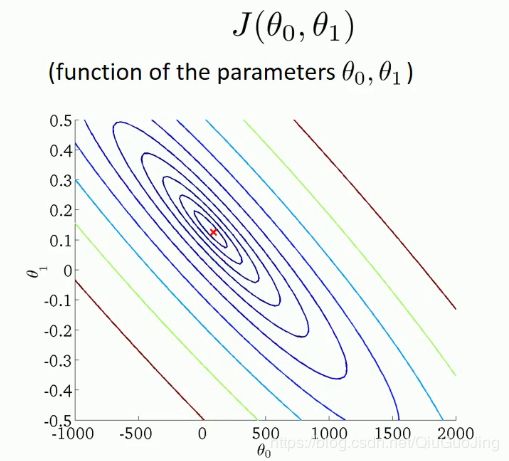
其中，关于的二维关系如下，在同一个等高线上的点所取得的代价函数相同。在图中的红点处取得最小值。

那么，在只有初始数据集和表达式的情况下，怎样找到最佳的使得最小？根据二元函数微分学的知识，我们知道要对进行求偏导。怎样操作呢？下面我们介绍一下梯度下降法。

更新的方法如下：

其中，上式中对分别求的偏导如下：

为什么随着迭代次数的增加，用梯度下降法能使取得最小值呢？我们从这个维度去看问题，如下图所示：

其中，学习率是正值，随着迭代次数的增加，函数的的图像越来越趋向于往最低谷走！同理从这个维度看问题也是一样！

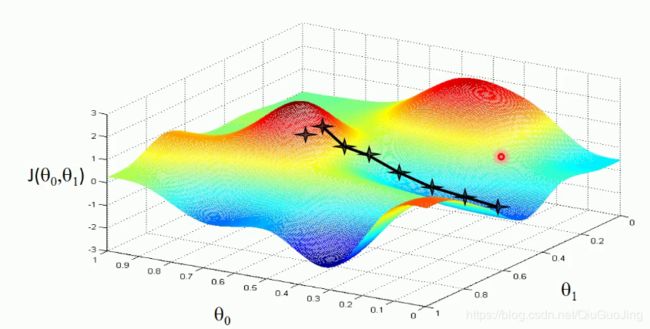
梯度下降法存在一个局限性，就是得到的最小值不一定是全局最小值，有可能是局部最小值。如下两图所示：

在上面的讨论中，我们得出在最小时的取值，也就是得出了我们所需要的这条回归直线方程的解析式。那么，怎样去评价这条回归线拟合程度的好坏呢？这个就要涉及两个概念了：相关系数和决定系数。

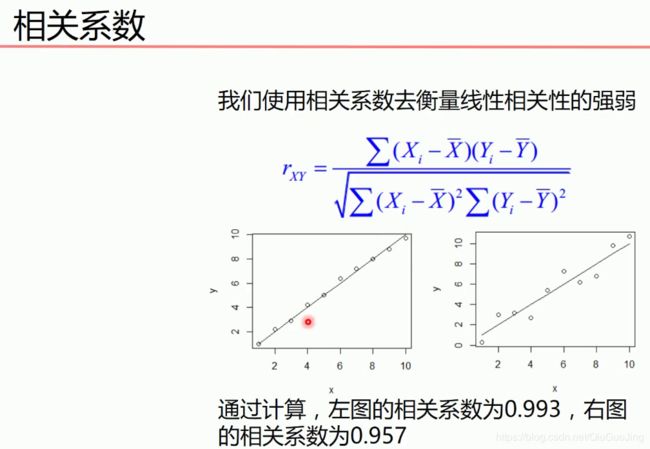
在上式中、表示的是所有样本点的平均值。由上面两个图可以看出，相关系数越接近1，样本点之间的关系越接近线性的关系（正相关）。相关系数越接近-1，样本点之间的关系越接近线性的关系（负相关）。

决定系数（coefficient  of determination）

相关系数是用来描述两个变量之间的线性关系的，但决定系数的适用范围更广。可以用来描述非线性或者有两个及两个以上自变量的相关关系。它也可以用来评价模型的效果！

上式中，是从样本点中取出来的值，称为真实值；是所有样本中真实值的平均值；是用回归方程得出的预测值。

的取值在0到1之间，越接近1，说明拟合程度越好！

下面用python来练习一下梯度下降法

   import numpy as np
   import matplotlib.pyplot as plt
    # 读取文件data.csv中的数据，并以逗号,为分隔符。
    data = np.genfromtxt("data.csv", delimiter=",")
    # x_data是数据集中的每一行的第0列，同理y_data是数据集中的每一行的第1列
    x_data = data[:,0]
    y_data = data[:,1]
    # scatter()方法是用来画散点图的。
    plt.scatter(x_data,y_data)
	# show()方法是将所画的图以图形界面的方式展现出来
    plt.show()
	
    # 学习率learning rate
    lr = 0.0001
    # 截距（初始化）
    b = 0 
    # 斜率（初始化）
    k = 0 
    # 最大迭代次数
    epochs = 50
    # 最小二乘法，计算代价函数
    def compute_error(b, k, x_data, y_data):
       totalError = 0
       for i in range(0, len(x_data)):
            totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
       return totalError / float(len(x_data)) / 2.0
    
	# 运行梯度下降法
    def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
        # 计算总数据量,
        m = float(len(x_data))
        # 循环epochs次
        for i in range(epochs):
            b_grad = 0
            k_grad = 0
            # 计算梯度的总和再求平均
            for j in range(0, len(x_data)):
                b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
                k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
            # 更新b和k
            b = b - (lr * b_grad)
            k = k - (lr * k_grad)
            # 每迭代5次，输出一次图像
            if i % 5==0:
                print("epochs:",i)
                plt.plot(x_data, y_data, 'b.')
                plt.plot(x_data, k*x_data + b, 'r')
                plt.show()
        return b, k
  
   
    print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
    print("Running...")
    b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
    print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))
   
    # 画图
     plt.plot(x_data, y_data, 'b.')         #表示用蓝色(blue)的点画图
     plt.plot(x_data, k*x_data + b, 'r')    #表示用红色(red)的线画图
     plt.show()
  

上面代码用到的data.csv文件截图如下：

如果调用python中的库sklearn的话，用几行代码就可以解决了。sklearn库包装了很多机器学习的算法。

    from sklearn.linear_model import LinearRegression    
    import numpy as np
    import matplotlib.pyplot as plt
   
    # 载入数据
    data = np.genfromtxt("data.csv", delimiter=",")
    x_data = data[:,0]
    y_data = data[:,1]
    plt.scatter(x_data,y_data)
    plt.show()
    print(x_data.shape)
  
    x_data = data[:,0,np.newaxis]
    y_data = data[:,1,np.newaxis]
    # 创建并拟合模型
    model = LinearRegression()
    model.fit(x_data, y_data)
   
   
    # 画图
    plt.plot(x_data, y_data, 'b.')
    plt.plot(x_data, model.predict(x_data), 'r')
    plt.show()