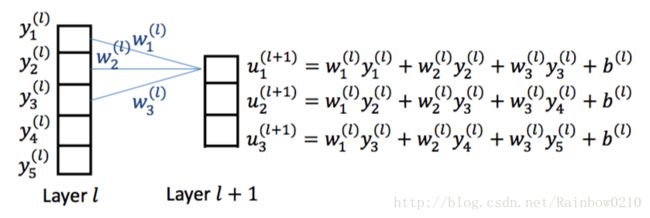深入理解卷积神经网络(CNN)——从原理到实现

王琦      QQ：451165431      计算机视觉&深度学习

转载请注明出处 ：http://blog.csdn.net/Rainbow0210/article/details/78562926。

本篇通过在MNIST上的实验，引出卷积神经网络相关问题，详细阐释其原理以及常用技巧、调参方法。欢迎讨论相关技术&学术问题，但谢绝拿来主义。

代码是博主自己写的，因为倾向于详细阐述底层原理，所以没有用TensorFlow等主流DL框架。实验结果与TF等框架可能稍有不同，其原因在于权重初始化方式的差异等，但并不影响对于网络的本质的理解。

---

实验概述

数据集

• MNIST：0-9共10个数字，其中，60000条训练样本，10000条测试样本，每条样本分辨率为 28×28 。拉伸为 1 维向量，因而为 28×28=784 维。

实验平台

• Python 2.7

实验内容

通过CNN完成对MNIST数据集的分类。具体有需要实现一下三部分：

• 卷积层：实现卷积层，包含 Conv2D, Relu, AvgPooled2D，其中，Relu 在作业一中已经实现
• 可视化：实现 第一个卷积层的可视化（经过 Relu 激活之后）
• 损失函数：实现 SoftmaxCrossEntropyLoss

实验原理

二维卷积 Conv2D

对于两个二维矩阵 I,K ，其卷积的数学表述为：

S(i,j)=(I∗K)(i,j)=∑m∑nI(m,n)⋅K(i−m,j−n)

其中， ∗ 表示卷积运算， ⋅ 表示点积。卷积运算满足交换律：

S(i,j)=(K∗I)(i,j)=∑m∑nI(i−m,j−n)⋅K(m,n)

由于在CNN中，卷积核往往是通过优化学习得到的，所以一般来讲，卷积和相关性是等价的：

S(i,j)=(K∗I)(i,j)=∑m∑nI(i+m,j+n)⋅K(m,n)

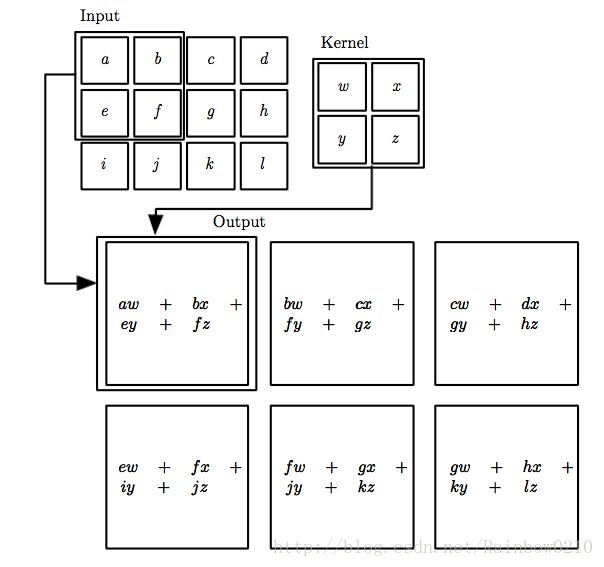
下图为相关性计算的示意图，卷积则只需将Kernel旋转 180∘ 即可：

池化 Pooling

将特征分为若干个相交/不相交的区域，再在每个区域上通过计算其最大值 (max-pooling) /均值 (average-pooling)，得到其池化特征。下图为最大池化 (max-pooling)的示意图：

罗杰斯特回归 Logistic Regression

对于一个二分类问题，设有两类 ω0,ω1 ，标签分别为 0,1 ，相应的网络只有一个输出神经元，则：

  P(t=1∣x)P(t=0∣x)=11+exp(−θT⋅x)≜h(x)=1−h(x)

其中， x 是样本， t∈(0,1) 是标签。对于包含 N 个独立同分布样本的数据集，记样本为 x(n) ，对应的标签为 t(n) ，有：

p(t(n)∣x(n),θ)=h(x(n))t(n)⋅(1−h(x(n)))(1−t(n))

由于样本满足独立同分布，所以

p(t(1),t(2),...,t(N)∣x(1),x(2),...,x(N),θ)=∏n=1Nh(x(n))t(n)⋅(1−h(x(n)))(1−t(n))

通过最大似然原理，使得上述概率密度最大，也就是使得下式取得最小（误差函数）：

E(θ)  ===−lnp(t(1),t(2),...,t(N)∣x(1),x(2),...,x(N),θ)−∑n=1N(t(n)⋅h(x(n))+(1−t(n))⋅(1−h(x(n))))∑n=1NE(θ)(n)

其中， E(θ)(n) 为交叉熵误差函数 (Cross-entropy Error Function)，定义如下：

E(θ)(n)=−t(n)⋅h(x(n))−(1−t(n))⋅(1−h(x(n)))

对于网络的训练阶段，是寻找合适的 θ 最小化上述损失函数；在网络的预测阶段，若 P(t=1∣x)>P(t=0∣x) ，则预测为 ω1 ，否则为 ω0 。

Softmax 回归 Softmax Regression

对于 K 分类问题（ K>2 ），标签为 K 位的 0−1 形式，即属于第 i 类，则第 i 位为 1 ，其他位为 0 。和罗杰斯特回归类似，定义：

hk(x)≜P(tk=1∣x,θ)=exp(θTk⋅x)∑Kj=1exp(θTj⋅x)

优化目标为：寻找一个合适的 θ ，使得：

• 当 x∈ωk 时， P(tk=1∣x,θ) 尽可能大
• 当 x∉ωk 时， P(tk=1∣x,θ) 尽可能小

Softmax 函数：

ϕ(zi)=ezi∑jezj∈(0,1)

值得注意的是：

∑iϕ(zi)=1

与罗杰斯特回归类似，可以定义包含 N 个样本的似然函数:

p(t(1),t(2),...,t(N)∣x(1),x(2),...,x(N),θ)=∏n=1N∏k=1KP(tk=1∣x(n),θ)t(n)k

同样，可以得到交叉熵损失函数：

E(θ)   ====−lnp(t(1),t(2),...,t(N)∣x(1),x(2),...,x(N),θ)−∑n=1N∑k=1K(t(n)⋅lnexp(θTk⋅x(n))∑Kj=1exp(θTj⋅x(n)))−∑n=1N∑k=1K(t(n)⋅lnh(n)k)∑n=1NE(θ)(n)

其中， E(θ)(n) 为交叉熵误差函数 (Cross-entropy Error Function)，定义如下：

E(θ)(n)=−∑k=1Kt(n)klnh(n)k

对于网络的训练阶段，是寻找合适的 θ 最小化上述损失函数；在网络的预测阶段，若 P(ti∣x)=maxjP(tj∣x) ，则预测为第 i 类。

卷积神经网络

其与全连接网络的主要区别在于：权值共享、局部互连、池化。在计算机视觉 (CV) 和自然语言处理 (NLP) 领域均有着广泛的应用。

前向传播

• 卷积层 Convolutional Layer:
  
  y(l+1)p=σ(y(l)p∗w(l)p+bp)
  
  其中， σ 是激活函数，在卷积神经网络中，常用 relu 激活函数:
  
  σ(x)=max(x,0)
• 池化层 Pooling Layer:
  
  y(l+1)p=pooling(y(l)p)
• 全连接层 Fully Connected Layer:
  
  y(l+1)=σ(y(l)⋅w(l)+b(l))
  
  若该全连接层为网络的最后一层，则激活函数通常为Softmax(Cross-entropy)或者Sigmoid(MSE)。

反向传播

• 误差函数：
  对于包含 N 个样本的数据集，定义误差函数：
  
  E=∑n=1NE(n)
  
  其中， E(n) 是第 n 个样本的误差函数。
  
  • MSE:
    
    E(n)=12∑k=1K(tk−y(L)k)2
  • Cross-entropy:
    
    E(n)=−∑k=1Ktk⋅lny(L)k

• 权值更新：
  

  w(l)j,i b(l)j==w(l)j,i−η⋅∂E∂w(l)j,ib(l)j−η⋅∂E∂b(l)j

• 权值衰减：
  定义代价函数：
  

  J=E+λ2⋅∑i,j,l(w(l)j,i)2
  
  此时权值更新应为：
  w(l)j,i b(l)j==w(l)j,i−η⋅∂J∂w(l)j,i=w(l)j,i−η⋅∂E∂w(l)j,i−λ⋅η⋅w(l)j,ib(l)j−η⋅∂J∂b(l)j=b(l)j−η⋅∂E∂b(l)j

• 局部梯度：
  定义局部梯度：
  

  δ(l)j=∂E(n)∂u(l)j
  
  值得注意的是，逐层梯度的传导：
  
  ∂y(l)i∂y(l−1)j=∑k=1m∂y(l)i∂u(l)k⋅∂u(l)k∂y(l−1)j

• 具体计算：

  • Convolutional Layer:
    简单起见，以一维卷积为例，我们计算下图的梯度：

    

    如图所示，网络的前一层有 5 个节点，后一层有 3 个节点，卷积核大小为 3 ，对应的运算关系如图。则可以得到局部梯度：
    

    δ(l)1 δ(l)2 ===∂E(n)∂u(l)1=∂E(n)∂u(l+1)1⋅∂u(l+1)1∂y(l)1⋅∂y(l)1∂u(l)1=δl+11⋅w(l)1⋅σ′(u(l)1)∂E(n)∂u(l)2=∂E(n)∂u(l+1)1⋅∂u(l+1)1∂y(l)2⋅∂y(l)2∂u(l)2+∂E(n)∂u(l+1)2⋅∂u(l+1)2∂y(l)2⋅∂y(l)2∂u(l)2δl+11⋅w(l)2⋅σ′(u(l)2)+δl+12⋅w(l)1⋅σ′(u(l)2)

    同理可以计算 δ(l)3,δ(l)4,δ(l)5 。得到如下结论：
    

    δ(l)=(δ(l+1)∗wl)⋅(σ′(u(l)))
    
    权值 w(l) 的梯度:
    ∂E(n)∂w(l)1 ∂E(n)∂w(l)2 ∂E(n)∂w(l)3===∑i=13∂E(n)∂u(l+1)i⋅∂u(l+1)i∂w(l)1=δ(l+1)1⋅y(l)1+δ(l+1)2⋅y(l)2+δ(l+1)3⋅y(l)3∑i=13∂E(n)∂u(l+1)i⋅∂u(l+1)i∂w(l)2=δ(l+1)1⋅y(l)2+δ(l+1)2⋅y(l)3+δ(l+1)3⋅y(l)4∑i=13∂E(n)∂u(l+1)i⋅∂u(l+1)i∂w(l)3=δ(l+1)1⋅y(l)3+δ(l+1)2⋅y(l)4+δ(l+1)3⋅y(l)5

    得到如下结论：
    

    ∂E(n)∂w(l) ∂E(n)∂b(l)==y(l)∗δ(l+1)∑i=13∂E(n)∂u(l+1)i⋅∂u(l+1)i∂b(l)=∑i=13δ(l+1)i

  • Average Pooling Layer:

    

    以上图为例，推倒局部梯度的计算：

    δ(l)1 δ(l)2==∂E(n)∂u(l)1=∂E(n)∂u(l+1)1⋅∂u(l+1)1∂y(l)1⋅∂y(l)1∂u(l)1=δ(l+1)1⋅12⋅σ′(u(l)1)∂E(n)∂u(l)2=∂E(n)∂u(l+1)1⋅∂u(l+1)1∂y(l)2⋅∂y(l)2∂u(l)2=δ(l+1)1⋅12⋅σ′(u(l)2)

    同理可得:

    δ(l)3=δl+12⋅12⋅σ′(u(l)3) δ(l)4=δl+12⋅12⋅σ′(u(l)4)

  • Max Pooling Layer:

    

    以上图为例，推倒局部梯度的计算：

    • 若 y(l)1≥y(l)2 ，
      
      δ(l)1 δ(l)2==∂E(n)∂u(l)1=∂E(n)∂u(l+1)1⋅∂u(l+1)1∂y(l)1⋅∂y(l)1∂u(l)1=δl+11⋅σ′(u(l)1)∂E(n)∂u(l)2=0

    • 否则
      

      δ(l)1 δ(l)2==∂E(n)∂u(l)1=0∂E(n)∂u(l)2=δl+11⋅σ′(u(l)2)

    • 若 y(l)3≥y(l)4 ，
      

      δ(l)3 δ(l)4==∂E(n)∂u(l)3=∂E(n)∂u(l+1)2⋅∂u(l+1)2∂y(l)3⋅∂y(l)3∂u(l)3=δl+12⋅σ′(u(l)3)∂E(n)∂u(l)4=0

    • 否则
      
      δ(l)3 δ(l)4==∂E(n)∂u(l)3=0∂E(n)∂u(l)4=δl+12⋅σ′(u(l)4)

    不妨假设 y(l)1≥y(l)2,y(l)3≥y(l)4 ，则：

    δ(l)1 δ(l)2 δ(l)3 δ(l)4====δl+11⋅σ′(u(l)1)0δl+12⋅σ′(u(l)3)0

代码实现

损失函数 SoftmaxCrossEntropyLoss

class SoftmaxCrossEntropyLoss(object):
    def __init__(self, name):
        self.name = name
        self.h = None

    def forward(self, input, target):
        exp_input = np.exp(input)
        sum = np.sum(exp_input, axis=1)
        h = np.divide(exp_input.T, sum).T
        self.h = h
        return np.mean(np.sum(- target * np.log(h), axis=1))

    def backward(self, input, target):
        return (self.h - target) / len(input)

卷积层

class Conv2D(Layer):
    def __init__(self, name, in_channel, out_channel, kernel_size, pad, init_std):
        super(Conv2D, self).__init__(name, trainable=True)
        self.kernel_size = kernel_size
        self.pad = pad
        self.W = np.random.randn(out_channel, in_channel, kernel_size, kernel_size) * init_std
        self.b = np.zeros(out_channel)

        self.diff_W = np.zeros(self.W.shape)
        self.diff_b = np.zeros(out_channel)

    def forward(self, input):
        self._saved_for_backward(input)
        output = conv2d_forward(input, self.W, self.b, self.kernel_size, self.pad)
        return output

    def backward(self, grad_output):
        input = self._saved_tensor
        grad_input, self.grad_W, self.grad_b = conv2d_backward(input, grad_output, self.W, self.b, self.kernel_size, self.pad)
        return grad_input

    def update(self, config):
        mm = config['momentum']
        lr = config['learning_rate']
        wd = config['weight_decay']

        self.diff_W = mm * self.diff_W + (self.grad_W + wd * self.W)
        self.W = self.W - lr * self.diff_W

        self.diff_b = mm * self.diff_b + (self.grad_b + wd * self.b)
        self.b = self.b - lr * self.diff_b

池化层

class AvgPool2D(Layer):
    def __init__(self, name, kernel_size, pad):
        super(AvgPool2D, self).__init__(name)
        self.kernel_size = kernel_size
        self.pad = pad

    def forward(self, input):
        self._saved_for_backward(input)
        output = avgpool2d_forward(input, self.kernel_size, self.pad)
        return output

    def backward(self, grad_output):
        input = self._saved_tensor
        grad_input = avgpool2d_backward(input, grad_output, self.kernel_size, self.pad)
        return grad_input

相关函数

def conv2d_forward(input, W, b, kernel_size, pad):
    '''
    Args:
        input: shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)
        W: weight, shape = c_out (#output channel) x c_in (#input channel) x k (#kernel_size) x k (#kernel_size)
        b: bias, shape = c_out
        kernel_size: size of the convolving kernel (or filter)
        pad: number of zero added to both sides of input

    Returns:
        output: shape = n (#sample) x c_out (#output channel) x h_out x w_out,
            where h_out, w_out is the height and width of output, after convolution
    '''
    h_out = input.shape[2] + 2 * pad - kernel_size + 1
    w_out = input.shape[3] + 2 * pad - kernel_size + 1
    c_out = W.shape[0]
    c_in = W.shape[1]
    input_col2 = im2col_cython(input, kernel_size, kernel_size, pad, 1)

    input_col2 = input_col2.T.reshape(h_out, w_out, input.shape[0], -1)
    w_col = W.reshape((c_out, c_in * kernel_size * kernel_size))
    output = np.dot(input_col2, w_col.T ) + b
    return output.transpose(2, 3, 0, 1)


def conv2d_backward(input, grad_output, W, b, kernel_size, pad):
    '''
    Args:
        input: shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)
        grad_output: shape = n (#sample) x c_out (#output channel) x h_out x w_out
        W: weight, shape = c_out (#output channel) x c_in (#input channel) x k (#kernel_size) x k (#kernel_size)
        b: bias, shape = c_out
        kernel_size: size of the convolving kernel (or filter)
        pad: number of zero added to both sides of input

    Returns:
        grad_input: gradient of input, shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)
        grad_W: gradient of W, shape = c_out (#output channel) x c_in (#input channel) x k (#kernel_size) x k (#kernel_size)
        grad_b: gradient of b, shape = c_out
    '''
    _, C_IN, H_IN, W_IN = input.shape
    _, C_OUT, H_OUT, W_OUT = grad_output.shape

    grad_output_col = im2col_cython(grad_output, kernel_size, kernel_size, kernel_size - 1, 1)
    h_padded = grad_output.shape[2] + kernel_size - 1
    w_padded = grad_output.shape[3] + kernel_size - 1
    grad_output_col = grad_output_col.T.reshape(h_padded, w_padded, grad_output.shape[0], -1)
    W_reshaped = np.rot90(W, 2, (2, 3)).transpose(1, 0, 2, 3).reshape(C_IN, -1)
    grad_input = np.dot(grad_output_col, W_reshaped.T).transpose(2, 3, 0, 1)
    grad_input = grad_input[:, :, pad: H_IN + pad, pad: W_IN + pad]

    input_col = im2col_cython(input.transpose(1, 0, 2, 3), H_OUT, H_OUT, pad, 1)
    h_padded = input.shape[2] + 2 * pad - H_OUT + 1
    w_padded = input.shape[3] + 2 * pad - H_OUT + 1
    input_col = input_col.T.reshape(h_padded, w_padded, input.shape[1], -1)
    grad_W = np.dot(input_col, grad_output.transpose(1, 0, 2, 3).reshape(C_OUT, -1).T).transpose(3, 2, 0, 1)

    grad_b = np.sum(grad_output, axis=(0, 2, 3))

    return grad_input, grad_W, grad_b

def avgpool2d_forward(input, kernel_size, pad):
    '''
    Args:
        input: shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)
        kernel_size: size of the window to take average over
        pad: number of zero added to both sides of input

    Returns:
        output: shape = n (#sample) x c_in (#input channel) x h_out x w_out,
            where h_out, w_out is the height and width of output, after average pooling over input
    '''
    input_padded = np.lib.pad(input, ((0,), (0,), (pad,), (pad,)), 'constant')
    output = block_reduce(input_padded, block_size=(1, 1, kernel_size, kernel_size), func=np.mean)
    return output


def avgpool2d_backward(input, grad_output, kernel_size, pad):
    '''
    Args:
        input: shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)
        grad_output: shape = n (#sample) x c_in (#input channel) x h_out x w_out
        kernel_size: size of the window to take average over
        pad: number of zero added to both sides of input

    Returns:
        grad_input: gradient of input, shape = n (#sample) x c_in (#input channel) x h_in (#height) x w_in (#width)

    '''
    grad_input = grad_output.repeat(kernel_size, axis=2).repeat(kernel_size, axis=3) / (kernel_size * kernel_size)
    return grad_input[:, :, pad: grad_output.shape[2] * kernel_size - pad, pad: grad_output.shape[3] * kernel_size - pad]

def im2col_cython(np.ndarray[DTYPE_t, ndim=4] x, int field_height,
                  int field_width, int padding, int stride):
    cdef int N = x.shape[0]
    cdef int C = x.shape[1]
    cdef int H = x.shape[2]
    cdef int W = x.shape[3]

    cdef int HH = (H + 2 * padding - field_height) / stride + 1
    cdef int WW = (W + 2 * padding - field_width) / stride + 1

    cdef int p = padding
    cdef np.ndarray[DTYPE_t, ndim=4] x_padded = np.pad(x,
            ((0, 0), (0, 0), (p, p), (p, p)), mode='constant')

    cdef np.ndarray[DTYPE_t, ndim=2] cols = np.zeros(
            (C * field_height * field_width, N * HH * WW))

    # Moving the inner loop to a C function with no bounds checking works, but does
    # not seem to help performance in any measurable way.

    im2col_cython_inner(cols, x_padded, N, C, H, W, HH, WW,
                        field_height, field_width, padding, stride)    
    return cols


@cython.boundscheck(False)
cdef int im2col_cython_inner(np.ndarray[DTYPE_t, ndim=2] cols,
                             np.ndarray[DTYPE_t, ndim=4] x_padded,
                             int N, int C, int H, int W, int HH, int WW,
                             int field_height, int field_width, int padding, int stride) except? -1:
    cdef int c, ii, jj, row, yy, xx, i, col

    for c in range(C):
        for ii in range(field_height):
            for jj in range(field_width):
                row = c * field_width * field_height + ii * field_height + jj
                for yy in range(HH):
                    for xx in range(WW):
                        for i in range(N):
                            col = yy * WW * N + xx * N + i
                            cols[row, col] = x_padded[i, c, stride * yy + ii, stride * xx + jj]

实验参数

网络结构

层序号	网络层类型	输入节点数	输出节点数	核大小
1	Conv2D	1*28*28	8*28*28	3*3
2	Relu	8*28*28	8*28*28	-
3	AvgPool2D	8*28*28	8*14*14	2*2
4	Conv2D	8*14*14	16*14*14	3*3
5	Relu	16*14*28	16*14*14	-
6	AvgPool2D	16*14*14	16*7*7	2*2
7	Reshape	16*7*7	784	-
8	Linear(FC)	784	256	-
9	Relu	256	256	-
10	Linear(FC)	256	10	-
11	Relu	10	10	-

相关参数

learning rate	weight_decay	momentum	epoch	batch_size
0.01	0.0001	0.9	100	100

实验结果

epoch	训练集loss	测试集loss	训练集accuracy	测试集accuracy
0	0.1224	0.1495	96.23	95.14
10	0.0341	0.0400	98.89	98.54
20	0.0149	0.0355	99.49	98.92
30	0.0117	0.0342	99.69	98.93
40	0.0075	0.0351	99.77	98.85
50	0.0049	0.0365	99.89	98.88
60	0.0037	0.0343	99.94	98.99
70	0.0029	0.0322	99.97	98.97
80	0.0024	0.0322	99.98	99.03
90	0.0023	0.0313	99.98	99.02
100	0.0022	0.0307	99.99	99.10

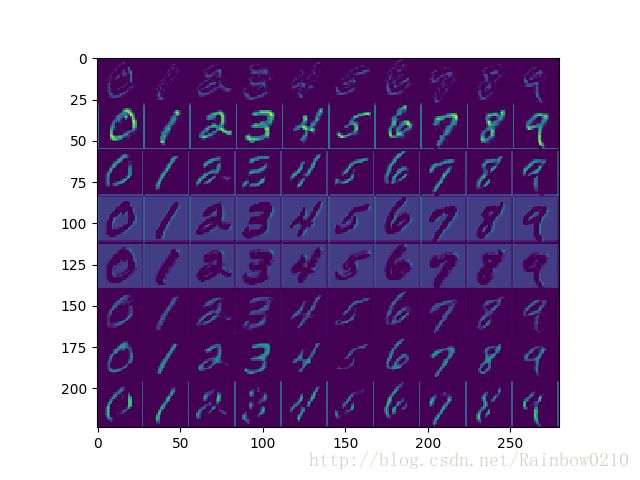
第一层卷积层的结果可视化：

从实验结果可以看出，相比于MLP的 98.67% 的test-accuracy，CNN的test-accuracy更高，可以达到 99.10% ，但是test-loss却不比MLP低,可能的原因是由于CNN的局部互连性，导致一些全局信息的丢失，但是这些信息对于分类结果却影响不大。在CPU上，CNN的训练速度远远慢于MLP，一个epoch大概需要 6 分钟，但是在相同的超参数设置下，有着更快的收敛速度， 20 个epoch就基本收敛。