运筹与决策(三)求解线性规划、运输问题和0-1整数规划问题
一、实验目的及要求
1、分别用excel、matlab和lingo求解线性规划、运输问题和0-1整数规划问题
2、撰写实验报告2
二、实验设备(环境)及要求
Microsoft Excel2016、matlab2017、lingo17
三、实验内容
线性规划
- 用excel求解
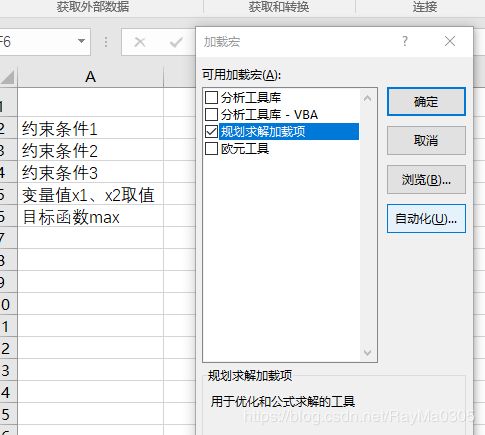
①加载宏—规划求解加载项
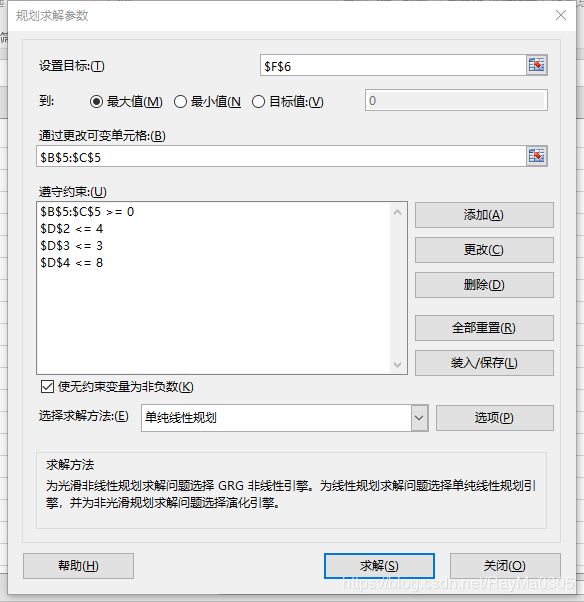
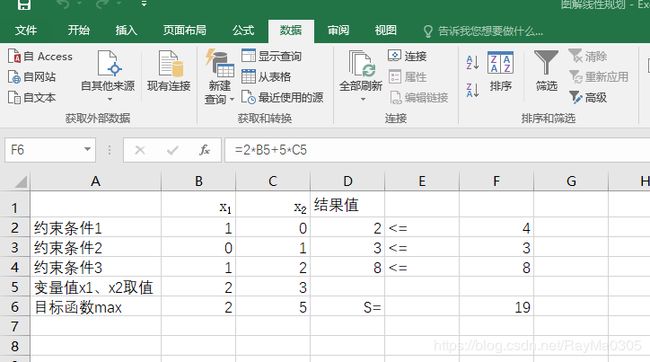
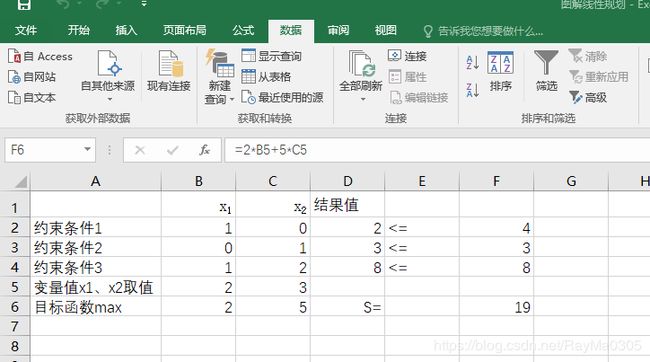
②根据分析题目填写约束条件、目标函数
D2=B5
D3=C5
D4=B5+2*C5
F6= =2*B5+5*C5
③添加线性求解
④求解结果
- matlab
max S=2x1+5x2
x1 ≤4
x2≤3
s.t. x1+ 2x2≤8
x1≥0
x2≥0
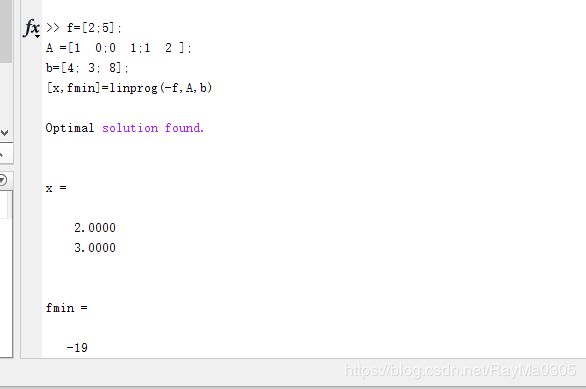
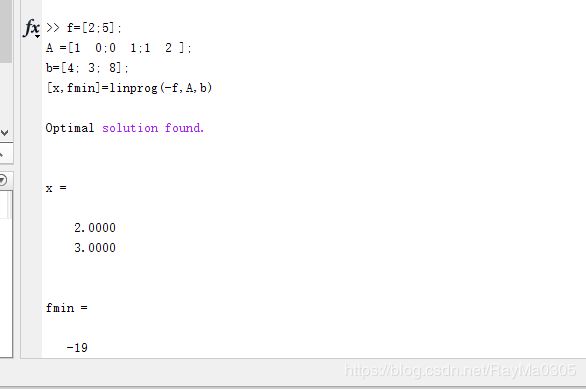
将目标函数转化为求函数-S的最小值,根据目标函数和约束条件,可以得出目标函数系数矩阵f=[2;5],不等式约束系数矩阵A =[1 0;0 1;1 2 ],不等式约束常向量b=[4; 3; 8], 调用MATLAB中lingprog函数求出-S的最小值,其相反数就是MaxS,如下图所示:
结果:
>> f=[2;5];
A =[1 0;0 1;1 2 ];
b=[4; 3; 8];
[x,fmin]=linprog(-f,A,b)
Optimal solution found.
x =
2.0000
3.0000
fmin =
-19
则MaxS=19
- lingo
代码:
max=2*X1+5*X2;
X1<=4;
X2<=3;
X1+2*X2<=8;
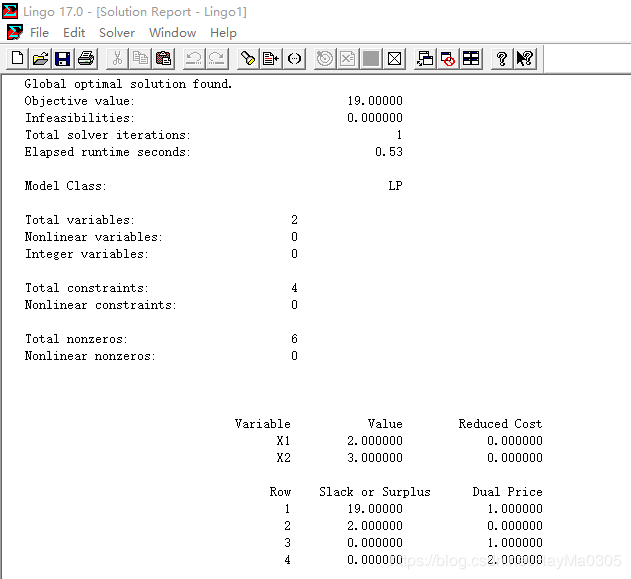
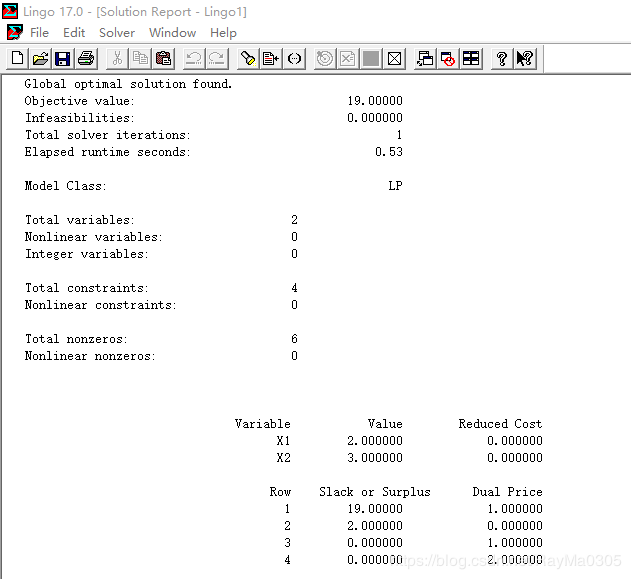
结果:
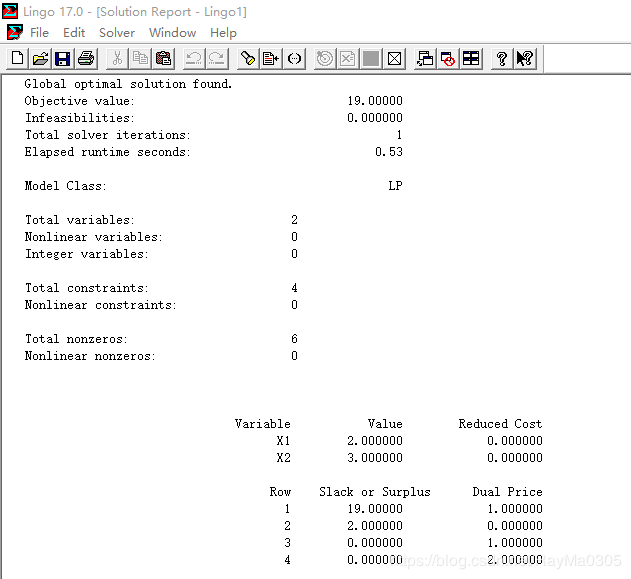
Global optimal solution found.
Objective value: 19.00000
Infeasibilities: 0.000000
Total solver iterations: 1
Elapsed runtime seconds: 0.53
Model Class: LP
Total variables: 2
Nonlinear variables: 0
Integer variables: 0
Total constraints: 4
Nonlinear constraints: 0
Total nonzeros: 6
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X1 2.000000 0.000000
X2 3.000000 0.000000
Row Slack or Surplus Dual Price
1 19.00000 1.000000
2 2.000000 0.000000
3 0.000000 1.000000
4 0.000000 2.000000
运输问题
Let xij = the number of truckloads to ship from cannery i to warehouse j
(i = 1, 2, 3; j = 1, 2, 3, 4)
Minimize Cost = $464x11 + $513x12 + $654x13 + $867x14
+ $352x21 + $416x22+ $690x23 + $791x24
+ $995x31 + $682x32 + $388x33 + $685x34
subject to
Cannery 1: x11 + x12 + x13 + x14 = 75
Cannery 2: x21 + x22 + x23 + x24 = 125
Cannery 3: x31 + x32 + x33 + x34 = 100
Warehouse 1: x11 + x21 + x31 = 80
Warehouse 2: x12 + x22 + x32 = 65
Warehouse 3: x13 + x23 + x33 = 70
Warehouse 4: x14 + x24 + x34 = 85
and xij ≥ 0 (i = 1, 2, 3; j = 1, 2, 3, 4)
- 用excel求解
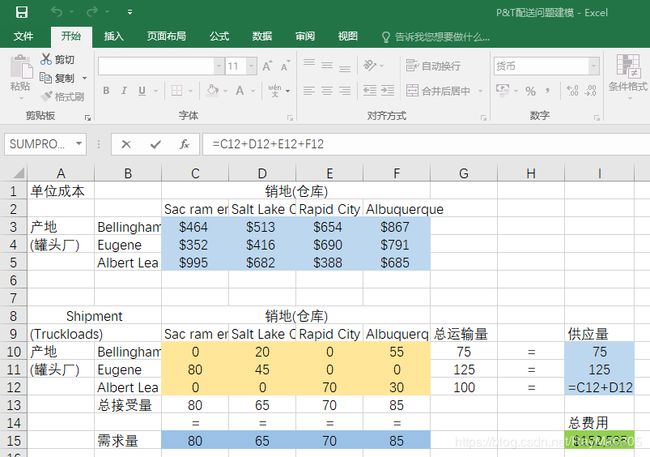
①输入问题的数据,
- 根据分析题目填写约束条件、目标函数
C15=C10+C11+C12
D15=D10+D11+D12
E15=E10+E11+E12
F15=F10+F11+F12
I10=C10+D10+E10+F10
I11=C11+D11+E11+F11
I12=C12+D12+E12+F12
I15=C3*C10+D3*D10+E3*E10+F3*F10+C4*C11+D4*D11+E4*E11+F4*F11+C5*C12+D5*D12+E5*E12+F5*F12
- 求解结果
- Matlab
函数Min Cost的值,根据目标函数和约束条件,可以得出目标函数系数矩阵f=[464 513 654 867 352 416 690 791 995 682 388 685],不等式约束系数矩阵A=[0 1 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0 0 1],不等式约束常向量b=[75 125 100 80 65 70 85], 调用MATLAB中lingprog函数求出Min Cost的值,如下图所示:
结果:
>> f=[464 513 654 867 352 416 690 791 995 682 388 685]
A=[0 1 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0 0 1]
b=[75 125 100 80 65 70 85]
c=[0 0 0 0 0 0 0 0 0 0 0 0 ];
[v,e]= linprog(f,[],[],A,b,c)
x=reshape(v,4,3);
x=x';
f =
464 513 654 867 352 416 690 791 995 682 388 685
A =
0 1 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0 0 1
b =
75 125 100 80 65 70 85
Optimal solution found.
v =
0
20
0
55
80
45
0
0
0
0
70
30
e =
152535
- Lingo
代码:
min=464*X11+513*X12+654*X13+867*X14
+352*X21+416*X22+690*X23+791*X24
+995*X31+682*X32+388*X33+685*X34;
X11+X12+X13+X14=75;
X21+X22+X23+X24=125;
X31+X32+X33+X34=100;
X11+X21+X31=80;
X12+X22+X32=65;
X13+X23+X33=70;
X14+X24+X34=85;
结果:
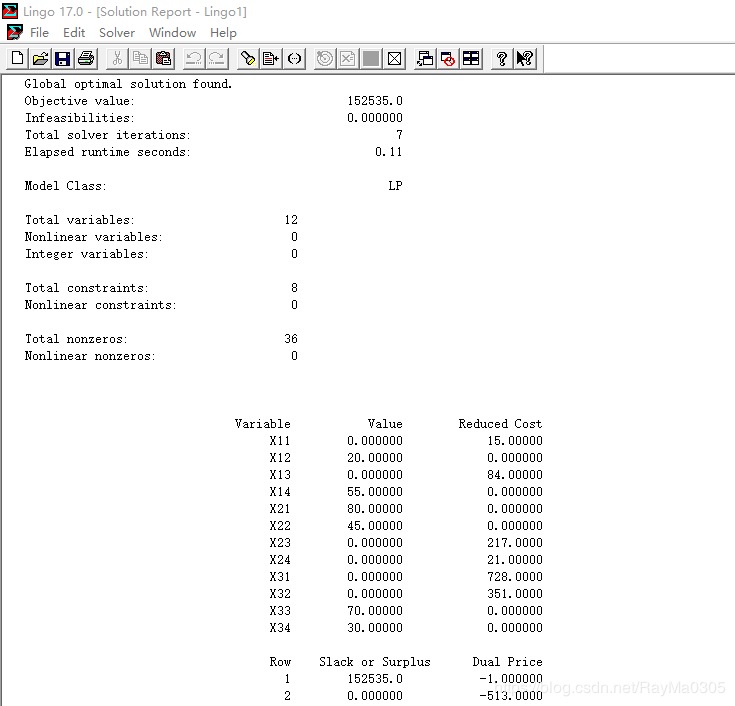
Global optimal solution found.
Objective value: 152535.0
Infeasibilities: 0.000000
Total solver iterations: 7
Elapsed runtime seconds: 0.11
Model Class: LP
Total variables: 12
Nonlinear variables: 0
Integer variables: 0
Total constraints: 8
Nonlinear constraints: 0
Total nonzeros: 36
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X11 0.000000 15.00000
X12 20.00000 0.000000
X13 0.000000 84.00000
X14 55.00000 0.000000
X21 80.00000 0.000000
X22 45.00000 0.000000
X23 0.000000 217.0000
X24 0.000000 21.00000
X31 0.000000 728.0000
X32 0.000000 351.0000
X33 70.00000 0.000000
X34 30.00000 0.000000
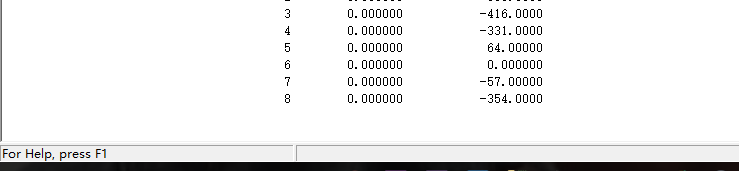
Row Slack or Surplus Dual Price
1 152535.0 -1.000000
2 0.000000 -513.0000
3 0.000000 -416.0000
4 0.000000 -331.0000
5 0.000000 64.00000
6 0.000000 0.000000
7 0.000000 -57.00000
8 0.000000 -354.0000
0-1整数规划问题
Maximize Z=9x1+5x2+6x3+4x4
Subject to
6x1+3x2+5x3+2x4≤10
x3+x4≤1
-x1 + x3 ≤0
-x1 +x4≤0
xj≤1
xj≥0
and
xj is integer, for j=1,2,3,4
xj is binary for j=1,2,3,4
- 用excel求解
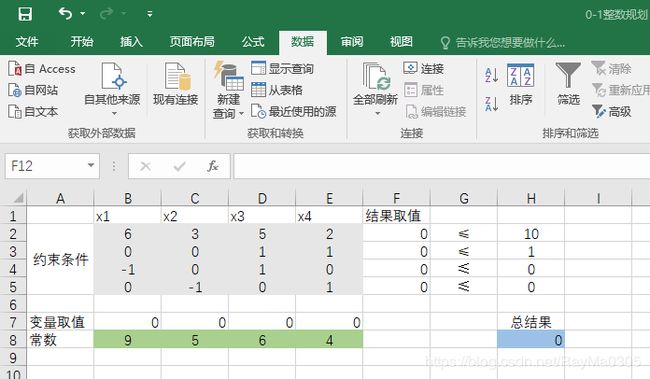
①输入问题数据
②分析题目添加约束条件、填写目标函数
F2 =B2*B7+C2*C7+D2*D7+E2*E7
F3 =D3*D7+E3*E7
F4 =B4*B7+D4*D7
F5 =C5*C7+E5*E7
B7=X1;C7=X2;D7=X3;E=X4
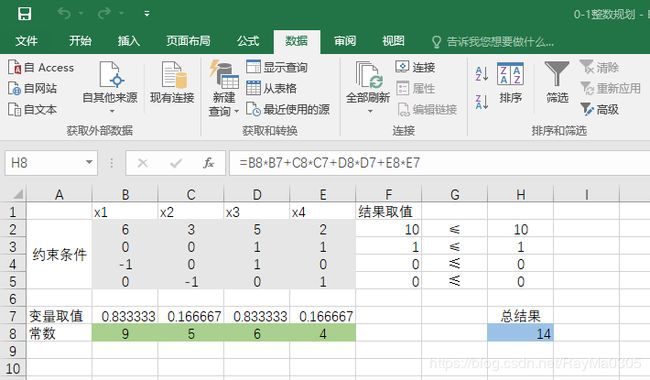
H8 =B8*B7+C8*C7+D8*D7+E8*E7
③求解结果:
- Matlab
将目标函数转化为求函数的f=-1*[9 5 6 4];根据目标函数和约束条件,可以得出目标函数系数矩阵A=[6 3 5 2
0 0 1 1
-1 0 1 0
0 -1 0 1]
b=[10 1 0 0];不等式约束常向量b=[10 1 0 0]; 调用MATLAB中intlinprog函数求出f的值,则-1*fval则为最终结果,如下图所示:
结果:
>> f=-1*[9 5 6 4];
intcon=[1 2 3 4];
A=[6 3 5 2
0 0 1 1
-1 0 1 0
0 -1 0 1]
b=[10 1 0 0];
lb=zeros(4,1);
ub=ones(4,1);
[x,fval,exitflag,output]=intlinprog(f,intcon,A,b,[],[],lb,ub);
x
-1*fval
A =
6 3 5 2
0 0 1 1
-1 0 1 0
0 -1 0 1
LP: Optimal objective value is -16.500000.
Cut Generation: Applied 1 implication cut.
Lower bound is -14.000000.
Relative gap is 0.00%.
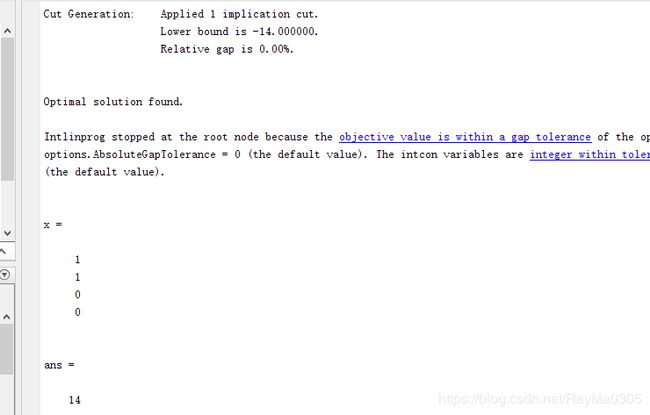
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05
(the default value).
x =
1
1
0
0
ans =
14
则结果为 14
3、lingo
代码:
max=9*x1+5*x2+6*x3+4*x4;
6*x1+3*x2+5*x3+2*x4<=10;
x3+x4<=1;
-x1+x3<=0;
-x1+x4<=0;
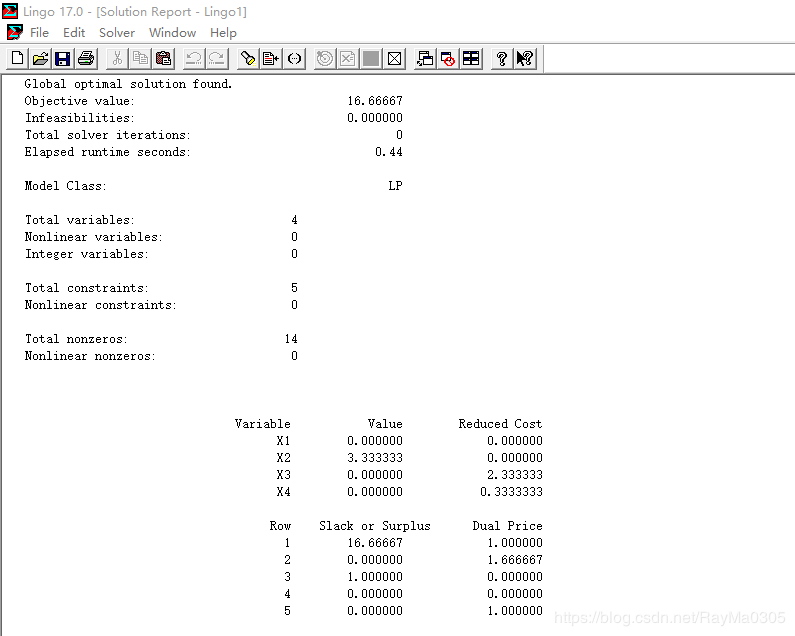
结果:
Global optimal solution found.
Objective value: 16.66667
Infeasibilities: 0.000000
Total solver iterations: 0
Elapsed runtime seconds: 0.44
Model Class: LP
Total variables: 4
Nonlinear variables: 0
Integer variables: 0
Total constraints: 5
Nonlinear constraints: 0
Total nonzeros: 14
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X1 0.000000 0.000000
X2 3.333333 0.000000
X3 0.000000 2.333333
X4 0.000000 0.3333333
Row Slack or Surplus Dual Price
1 16.66667 1.000000
2 0.000000 1.666667
3 1.000000 0.000000
4 0.000000 0.000000
5 0.000000 1.000000
结果为14
四、实验结果
线性规划:
Excel:
MATLAB:
LINGO:
运输问题:
Excel:
MATLAB:
LINGO:
0-1整数规划:
Excel:
MATLAB:
LINGO:
五、分析与讨论
这次实验分别用excel、matlab和lingo求解线性规划、运输问题和0-1整数规划问题,相比第一次实验,这次实验学习了lingo这个计算机软件工具,用不同的工具去求解问题。 线性规划问题是使用linprog函数将目标函数求Max值转化为求函数-S的最小值;运输问题调用matlab中lingprog函数求出Min Cost的值;求解0-1整数问题时,在使用matlab时,使用了intlinprog函数。
本次实验实践过程较为轻松,首先要明确问题类型,分析题目,理解题目的约束条件、目标函数,熟悉Excel、matlab、lingo软件的公式或函数,就能轻松把结果求解出来。