【PyTorch学习笔记】9：感知机,链式法则,对Himmelblau函数的优化实例

感知机

单层感知机的例子

import torch
from torch.nn import functional as F

x = torch.randn(1, 10)
w = torch.randn(1, 10, requires_grad=True)
# 对输出用sigmoid激活
o = torch.sigmoid(x @ w.t())
print("输出值:", o)
# 计算MSE
loss = F.mse_loss(torch.ones(1, 1), o)
print("损失:", loss)
# 计算梯度
loss.backward()
print("损失对w的导数:", w.grad)

运行结果：

输出值: tensor([[0.9352]], grad_fn=)
损失: tensor(0.0042, grad_fn=)
损失对w的导数: tensor([[-0.0051, -0.0106,  0.0006, -0.0090, -0.0068, -0.0035,  0.0017,  0.0010,
         -0.0099,  0.0064]])

多层感知机的例子

就只要设置多组w，即为w这个Tensor前面添加一个"组"的维度即可。

import torch
from torch.nn import functional as F

x = torch.randn(1, 10)
# 这里有两组w,也就输出到了2个结点上
w = torch.randn(2, 10, requires_grad=True)
# 对输出用sigmoid激活
o = torch.sigmoid(x @ w.t())
print("输出值:", o)
# 计算MSE
loss = F.mse_loss(torch.ones(1, 1), o)  # 这里自动广播成了size=1,2的Tensor再进行计算
print("损失:", loss)
# 计算梯度
loss.backward()
print("损失对w的导数:", w.grad)

运行结果：

输出值: tensor([[0.9790, 0.0207]], grad_fn=)
损失: tensor(0.4798, grad_fn=)
损失对w的导数: tensor([[-2.8575e-04, -6.2913e-04,  1.5963e-04,  2.8028e-04, -8.5252e-04,
         -3.1425e-04,  3.1833e-04, -3.9444e-04, -1.7871e-04, -6.8897e-05],
        [-1.3182e-02, -2.9024e-02,  7.3644e-03,  1.2930e-02, -3.9330e-02,
         -1.4498e-02,  1.4686e-02, -1.8197e-02, -8.2446e-03, -3.1785e-03]])

链式法则

x经过参数w1和b1得到y1，y1再通过w2和b2得到y2，要求y2对w1的导数，可以求y2对y1然后y1对w1的导数。PyTorch可以自动使用链式法则对复杂的导数求解。

import torch

x = torch.tensor(1.2)
w1 = torch.tensor(2.3, requires_grad=True)
b1 = torch.tensor(1.3)
y1 = x * w1 + b1

w2 = torch.tensor(2.2)
b2 = torch.tensor(1.4)
y2 = y1 * w2 + b2

# PyTorch自动实现链式法则的求导
dy2_dw1 = torch.autograd.grad(y2, [w1], retain_graph=True)
print(dy2_dw1[0])

# 手动用链式法则的方式求一下看看
dy2_dy1 = torch.autograd.grad(y2, [y1], retain_graph=True)
dy1_dw1 = torch.autograd.grad(y1, [w1], retain_graph=True)
print(dy2_dy1[0] * dy1_dw1[0])

运行结果：

tensor(2.6400)
tensor(2.6400)

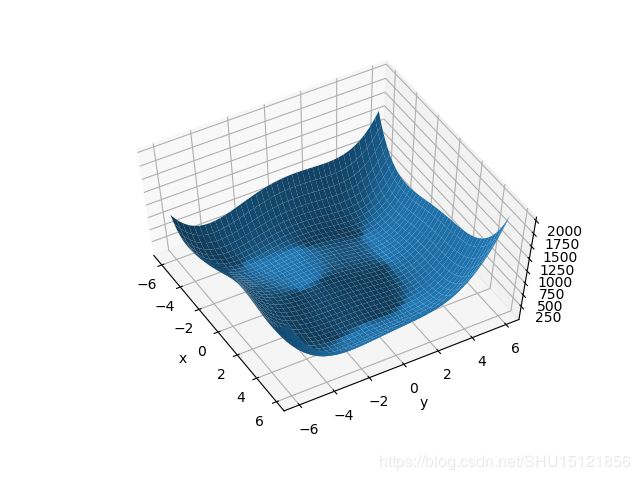
对Himmelblau函数的优化实例

Himmelblau函数如下：
$$f(x,y)=(x^2+y-11{)}^2+(x+y^2-7{)}^2$$
它有四个局部最小值，且值都为0，这个函数常用来检验优化算法的表现如何。

可视化3D图像

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def himmelblau(x):
	return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2


x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
X, Y = np.meshgrid(x, y)
Z = himmelblau([X, Y])
fig = plt.figure("himmeblau")
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

运行结果：

使用随机梯度下降优化

import torch


def himmelblau(x):
	return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2


# 初始设置为0,0.
x = torch.tensor([0., 0.], requires_grad=True)
# 优化目标是找到使himmelblau函数值最小的坐标x[0],x[1]
# 这里是定义Adam优化器,指明优化目标是x,学习率是1e-3
optimizer = torch.optim.Adam([x], lr=1e-3)

for step in range(20000):
	# 每次计算出当前的函数值
	pred = himmelblau(x)
	# 当网络参量进行反馈时,梯度是被积累的而不是被替换掉,这里即每次将梯度设置为0
	optimizer.zero_grad()
	# 生成当前所在点函数值相关的梯度信息,这里即优化目标的梯度信息
	pred.backward()
	# 使用梯度信息更新优化目标的值,即更新x[0]和x[1]
	optimizer.step()
	# 每2000次输出一下当前情况
	if step % 2000 == 0:
		print("step={},x={},f(x)={}".format(step, x.tolist(), pred.item()))

运行结果：

step=0,x=[0.0009999999310821295, 0.0009999999310821295],f(x)=170.0
step=2000,x=[2.3331806659698486, 1.9540692567825317],f(x)=13.730920791625977
step=4000,x=[2.9820079803466797, 2.0270984172821045],f(x)=0.014858869835734367
step=6000,x=[2.999983549118042, 2.0000221729278564],f(x)=1.1074007488787174e-08
step=8000,x=[2.9999938011169434, 2.0000083446502686],f(x)=1.5572823031106964e-09
step=10000,x=[2.999997854232788, 2.000002861022949],f(x)=1.8189894035458565e-10
step=12000,x=[2.9999992847442627, 2.0000009536743164],f(x)=1.6370904631912708e-11
step=14000,x=[2.999999761581421, 2.000000238418579],f(x)=1.8189894035458565e-12
step=16000,x=[3.0, 2.0],f(x)=0.0
step=18000,x=[3.0, 2.0],f(x)=0.0