论文解读: Quantized Convolutional Neural Networks for Mobile Devices

关注SIGAI公众号，获取更多技术文章及资源

PDF全文地址：http://tensorinfinity.com/paper_118.html

论文地址：https://arxiv.org/abs/1512.06473
源码地址：https://github.com/jiaxiang-wu/quantized-cnn

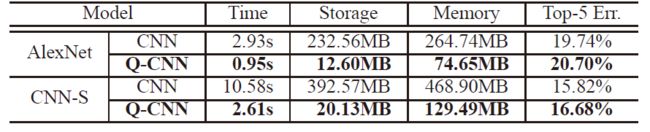
CNN网络在许多方面发挥着越来越重要的作用，但是CNN模型普遍很大，计算复杂，对硬件的要求很高，这也是限制CNN发展的一个因素。在这篇论文中，作者提出了一个加速和压缩CNN的方法——Quantized CNN，主要思想是对卷积层和全连接层中的权重进行量化，并最小化每层的响应误差。作者也在ILSVRC-12上做了大量的实验，证明对于分类任务在仅损失很小的准确率下，该方法可以达到4-6倍的加速，和15~20倍的压缩。作者也在实际手机设备中进行了实验，对于移动设备（华为Mate7）可以在1s内准确分类图片，其效果如图1所示。红色为原始网络的效果，蓝色为量化后的网络的效果。第一张图是耗时的比较，第二张图是存储空间的比较，第三张图是forward过程占用内存的比较，第四张图是错误率比较。发现该方法确实可以对CNN网络有很好的加速和压缩效果，同时并没有增加很多错误率。

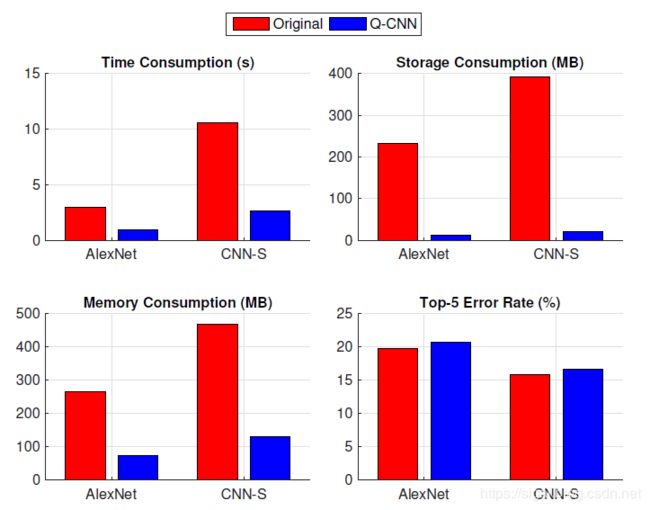
图1 华为Mate7手机上AlexNet，CNN-S两个网络在量化前后的耗时、存储和准确率

一.简介

目前CNN网络尽管取得了很成功的发展，模型准确率在很多方面都远远高于传统方法，但是其参数个数，和计算复杂度始终是制约其快速发展的一个因素，例如8层的AlexNet就有60M参数，在分类一张图需要729M的浮点操作个数，尽管训练过程可以离线进行，GPU也可以有很好的加速效果，但是对于一般的个人电脑和移动设备，仅仅是测试中的forward过程就已经十分吃力，甚至是无法负担这样巨大的计算需求，再加上移动设备上存储条件的限制，当前很多效果很好的深度学习模型无法在移动端实现。因此网络模型的加速和压缩至关重要。
对于大多的CNN网络，卷积层是最耗时的部分，全连接层则是最占存储空间的部分，由于这两者在CNN网络的复杂度和空间占用上存在本质上的不同，因此大多的工作是针对其一进行的，比如【7，13，32，31，18，17】低秩估计和矩阵分解方法用于加速卷积层，另一方面【3，7，11，30，2，12，28】则针对全连接层研究参数压缩的方法。总体看上述工作都仅仅完成了加速网络，或压缩参数中的一个工作，却没有同时做加速和压缩。
本文提出的方法Quantized CNN（Q-CNN）可以在很小的准确率损失下同时加速和压缩CNN模型。该方法的核心是对参数进行量化（用少部分的参数来表示全体参数），并通过内积运算来估计卷积层和全连接层的输出。为保证准确率，该方法在参数量化过程中最小化每层输出的估计误差。同时为了减少多层量化导致的误差累积，本文采用的策略是每层的优化目标中考虑之前的估计误差。
第二节将先叙述一些基础知识，第三节将详细叙述本文提出的方法，第四节是相关实验部分，作者在MNIST，ILSVRC-12上分别进行了实验，针对AlexNet，CaffeNet，CNN-S，VGG16网络结构进行量化，总体实验结果表明，对每一种网络，Quantized CNN都可以达到4倍的加速，和15倍的压缩，并保证Top-5准确率下降不到1%。最后作者在实际的手机上也进行了实验，证明了该方法的实际效果。

二.基础

## 卷积的本质

在测试部分（也即推理过程中）由于大部分的计算在卷积层部分，而大部分的参数在全连接层部分，因此为了得到最有效率的forward过程，我们可以重点加速卷积层的计算，压缩全连接层的参数。
在CNN网络中，其实卷积操作和全连接操作都是通过矩阵乘法实现的（在视频中有详细介绍，im2col过程），而矩阵的乘法实际就是若干向量内积。那么我们如果将卷积层的输入特征图设为S，输出特征图设为T，且两个特征图的维度分别为
$S\in {\mathbb{R}}^{d_s\times d_s\times C_s},T\in {\mathbb{R}}^{d_t\times d_t\times C_t}$
其中$d_s$,$d_t$分别为输入、输出特征图的尺寸（这里以正方形图为例），$C_s$,$C_t$分别为输入、输出特征图的通道数，那么对于输出特征图，在${\rho }_s$位置，第$c_t$个通道的值（标量）可以通过如下计算表示
$T_{p_t}(c_t)={\sum }_{{\rho }_t,{\rho }_s}⟨W_{c_t,{\rho }_k},S_{{\rho }_s}⟩$
式中$W_{c_t}\in {\mathbb{R}}^{d_k\times d_k\times C_s}$表示第$C_t$个filter，$d_k$表示卷积kernel size的大小。${\rho }_k,{\rho }_s\in {\mathbb{R}}^2$分别表示卷积参数和输入特征图的2维空间位置，$W_{c_t,{\rho }_k},S_{{\rho }_s}\in {\mathbb{R}}^{C_s}$，都是向量，$⟨W_{c_t,{\rho }_k},S_{{\rho }_s}⟩$则表示两个向量的内积，而卷积结果$T_{{\rho }_t}(C_t)$（标量）实际上是$d_k\times d_k$个内积的和。（值得注意的是，${\rho }_s$是在输入特征图上取$d_k\times d_k$个位置，在累加过程中和$p_k$变化是相同的，也即这个累加的次数为$d_k\times d_k$，具体过程在视频中im2col过程有介绍）
而对于全连接层，没有空间位置（spatial）的维度，因此第c_t个通道的值可以通过如下计算表示
$T(C_t)=⟨W_{C_t},S⟩$
其中$S\in {\mathbb{R}}^{C_s},T\in {\mathbb{R}}^{C_t},W_{C_t}\in {\mathbb{R}}^{C_s}$，分别表示输入特征图，输出特征图，参数中第$C_t$个filter

## 乘积量化

乘积量化在估计最近邻居的搜索中广泛应用，且有很好的效果。其思想是将一个特征空间分解成若干子空间的笛卡儿积（直积），其实很简单的概念，比如二维空间（x,y），拆分成两个子空间（x）和（y）。笛卡尔积的公式如下
$A\otimes B=\left\{(x,y)\mid x\in A,y\in B\right\}$
而乘积量化并不是仅仅拆分成两个子空间，而是拆分成多个子空间，不过定义是一样的。拆分后对每一个子空间，学习一个码书（用于量化该子空间中的所有向量），那么原特征空间中的任一向量都可以用所有子空间码书中的某个向量，做级联表示。
以图2.1所示，上面的向量为原本特征空间下的特征向量，我们将其拆分成m个子特征空间，如下面每行所示，每一行都对应一个子空间。倘若我们对每一个子空间都学习一个码书（可以看作一堆聚类中心向量，并按顺序排列，带有索引，那么我就可以根据索引来直接引用某一个聚类中心向量）那么每一个子空间中的向量（图2.1中的每一行）都可以用码书中的某一个聚类中心来表示，那么我们直接可以用索引来表示原本的向量就可以了（例如第一行的向量对应可以用第一个码书中的第$k_1$个聚类中心表示，di二行的向量可以用第二个码书中的第$k_2$个聚类中心表示，以此类推…，那么原本的向量就可以表示为$k_1$ $k_2$… $k_m$，这样可以减少存储数据占用的空间，当然我们还是需要额外的空间来存储每个子空间中的码书）。

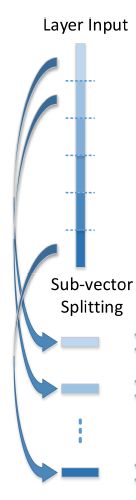
图2.1 乘积量化的示意图
在本文中，即利用乘积量化来优化内积计算，假设两个向量分别为$x,y\in {\mathbb{R}}^D$，首先我们将两个向量都分解成M个子向量，表示为$x^m,y^m\in {\mathbb{R}}^{D/M}$m=1,2,…M，同时每个$x^m$都可以用第m个码书中第$k_m$个向量表示（这种过程就是量化），那么原内积计算可以表示为
$⟨y,x⟩={\sum }_{m=1}^M⟨y^m,x^m⟩\approx {\sum }_{m=1}^M⟨y^m,c_{k_m}^m⟩$
如此我们可以将复杂度为O(D)的内积运算转化为M个加法运算（注意，我们预先计算好$y^m$与第m个码书中所有向量的内积）

三.Quantized CNN

在本节将首先详细叙述Quantized CNN的量化过程，分别叙述全连接层和卷积层的量化过程；其次，本文证明通过直接最小化每层的估计误差，可以得到更好的量化，以保证准确率；最后，作者分析了Quantized CNN模型的计算复杂度。
全连接层的量化
对于全连接层，设权重矩阵为$W\in {\mathbb{R}}^{C_s\times C_t}$，其中$C_s$,$C_t$分别表示输入通道数和输出通道数，$W_{c_t}$表示第$c_t$个filter，即W的第$C_t$列，如图3.1所示
现在对输入维度$C_s$拆分成M个子空间，设$C_s^{{}^{\prime }}=C_s/M$，权重矩阵$W=W^1\otimes W^2\otimes ...\otimes W^m$,每个$W_{C_t}$拆分成M个子向量，设为$W_{c_t}^m$,m=1,2,…,M，如图3.1所示，即每个虚线隔开的就是一个在每一个子空间中（图3.1中Weight Matrix虚线之间的一行）其实由$C_t$个列向量组成，我们可以对每一个子空间都学习一个码书$B^m$，包含K个聚类中心，那么对于$W_{c_t}^m$，可以用码书中的某个向量来近似表示
$D^m\in {\mathbb{R}}^{C_s^{{}^{\prime }}\times K}$
现在子空间中每个向量$W_{c_t}^m$都对应于码书矩阵$D^m$中的一个索引，设索引矩阵为$B^m$，值为0或1，则有
$B^m\in {\left\{0,1\right\}}^{k\times C_t}$
于是对参数矩阵的估计可以表示为
${\tilde{W}}^m=D^m{B}^m\approx W^m$
我们希望权重参数的估计误差最小，即最优化目标如下所示，对于该目标函数的求解将在后面（对量化的误差修正）介绍
$$\begin{gathered} {\min }_{D^{(m)},\left\{B_{p_k}^{(m)}\right\}}{\sum }_{p_k}{\Vert D^{(m)}{B}_{p_k}^{(m)}-W_{p_k}^{(m)}\Vert }_F^2 \\ s.t.D^m\in \in {\mathbb{R}}^{C_s^{{}^{\prime }}\times K},B^m\in {\left\{0,1\right\}}^{K\times C_t} \end{gathered}$$
那么输出特征图即可用码书和索引矩阵来估计，即
$T(C_t)={\sum }_{m=1}^M⟨W_{C_t}^m,S^m⟩\approx {\sum }_{m=1}^M⟨D^m{B}_{ct}^m,S^m⟩={\sum }_{m=1}^M⟨D_{k_m(c_t)}^m,S^m⟩$
式中$B_{c_t}^m$表示$W_{c_t}^m$向量在码书中的索引（注意$B_{c_t}^m$向量是one-hot的形式，索引i即第i位为1，其他位为0组成的向量）,$k_m(c_t)$表示$W_{c_t}^m$对应码书中的索引，$D_{k_m(c_t)}^m$即为估计$W_{C_t}^m$的向量（注意在实际运算中$⟨D_{k_m(c_t)}^m,S^m⟩$是提前计算好的，也就是在这一步可以减少计算量）
现在我们来看计算复杂度，若要计算原本全连接层，复杂度为$O(C_s{C}_t)$（全连接层的计算由$C_t$个内积组成，每个内积需要计算$C_s$个乘法和加法），而经过量化后，其复杂度变为$O(C_{s}K+C_{t}M)$，$O(C_{s}K)$对应输入向量与码书中所有向量内积的复杂度，$O(C_{t}M)$对应$C_{t}M$个加法。

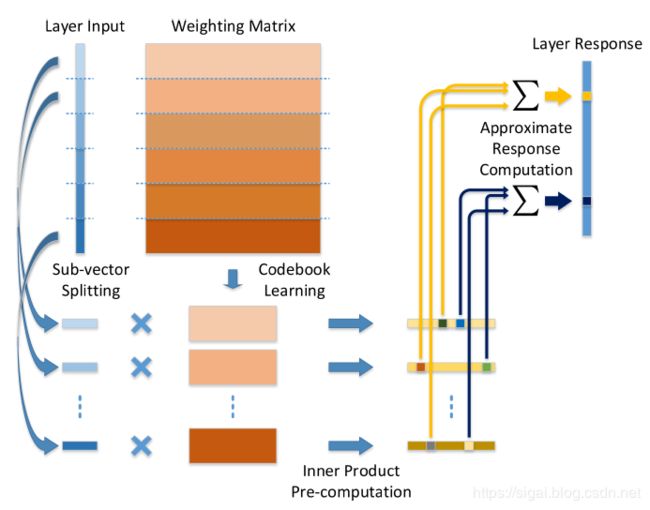
图3.1 全连接层的量化示意图

## 卷积层的量化

对卷积层的量化可以类比对全连接层的量化，但是权重不再是矩阵，而是一个张量W\in ${\mathbb{R}}^{d_k\times d_k\times C_s}$，同时卷积操作因为滑动窗的缘故，在计算时会有重复计算，属于冗余操作，而这里我们在提前计算输入向量与码书中向量内积的时候是没有冗余的，实际上也可以大大提高计算效率。对于卷积层，量化目标为
$$\begin{gathered} {\min }_{D^m,B_{p_k}^m}{\sum }_{p_k}{\Vert D^m{B}_{p_k}^m-W_{p_k}^m\Vert }_F^2 \\ s.t.D^m\in {\mathbb{R}}^{C_s^{{}^{\prime }}\times K},B_{p_k}^m\in {\left\{0,1\right\}}^{K\times C_t} \end{gathered}$$
这里$W_{p_k}^m\in {\mathbb{R}}^{C_S^{{}^{\prime }}\times K}$，表示在$p_k$位置上第m个子空间下的参数（这里可以参考第二节基础中卷积的本质中的部分）对于输出特征图的估计，可以表示为
$$\begin{array}{rl}{T}_{pt}(c_t)& =\sum _{(p_k,p_s)}\sum _{m=1}^M⟨W_{c_t,p_k}^m,S_{p_s}^m⟩\\ & \approx \sum _{(p_k,p_s)}\sum _{m=1}^M⟨D^m{B}_{c_t,p_k}^m,S_{p_s}^m⟩\\ & =\sum _{(p_k,p_s)}\sum _{m=1}^M⟨D_{k_{m(c_t,p_k)}}^m,S_{p_s}^m⟩\end{array}$$

## 对量化的误差修正

通过前面介绍的步骤，其实是可以减少参数存储和整体forward的计算量，但是直接学习到的码书和索引其实是有误差的，直接用量化后的模型做预测，其准确率会差很多，所以在这一节里将介绍对码书和索引的调优，以保证准确率。优化目标是最小化输出特征图的重建误差（类似之前pruning那篇论文的优化目标），因为单纯最小化参数量化误差很可能不会对准确率有很大的影响，但是最小化输出特征图的重建误差，就是对准确率的直接优化。
首先我们以全连接层为例，假设我们一共有N张图片，某层的输入，输出特征图分别是$S_n$,$T_n$，为了最小化输出特征图重建误差，有一下优化目标
${\min }_{{\left\{D^m\right\}}_m^{{}^{\prime }}{\left\{B^m\right\}}_m}{\sum }_{n=1}^N{\Vert T_n-{\sum }_{m=1}^M(D^m{B}^m{)}^T{S}_n^m\Vert }_F^2$ （3.1）

上式中，前一项是该全连接层原本的输出特征图，后一项是经过量化后的输出特征图，注意我们需要优化的是$D^m$,$B^m$,m=1,2,…,M。 然而$D^m$,$B^m$对于不同的m，是互补相关的（因为不同的m对应不同的子空间）如果我们一次仅优化一个$D^m$,$B^m$，那么问题可以得到简化。我们先定义一个变量
$R_n^m=T_n-{\sum }_{m^{{}^{\prime }}=1,m^{{}^{\prime }}̸=m}^M(D^{m^{{}^{\prime }}}{B}^{m^{{}^{\prime }}}{)}^T{S}_n^{m^{{}^{\prime }}}$
那么当我们仅优化$D^m$,$B^m$时，式（3.1）可以简化为
${\min }_{D^m,B^m}{\sum }_{n=1}^N{\Vert R_n^m-(D^m{B}^m{)}^T{S}_n^m\Vert }_F^2$ （3.2）

上述优化问题可以通过两步迭代的方式，分别求解$D^m$和$B^m$

## 更新D^m（码书）

在这一步，我们固定$B^m$（索引），并定义$L_k=\left\{C_t\mid B^m(k,C_t)=1\right\}$，因为原本$B^m$的列向量是oe-hot形式，现在$L_k$就是$B^m$列向量中为索引为k的所有向量（注意k表示码书中的索引，最多K个），于是式（3.2）可以写作
${\min }_{{\left\{D_k^m\right\}}_k}{\sum }_{n=1}^N{\sum }_{k=1}^K{\sum }_{C_t\in L_k}{\left[R_n^m(C_t)-(D_k^m{)}^T{S}_n^m)\right]}^2$
在这一步，我们同样发现，我们在更新码书中的s个聚类中心时，其实是相互独立的，所以我们可以分别更新$D_k^m$,k=1,2,…,K，即
${\min }_{D_k^m}{\sum }_{n=1}^N{\sum }_{C_t\in L_k}{\left[R_n^m(C_t)-(D_k^m{)}^T{S}_n^m)\right]}^2$

更新B^m（索引）

在这一步，我们固定$D^m$(码书)，于是式（3.2）可以写作
$k_m^{\ast }(C_t)=argmi{n}_k{\sum }_{n=1}^N{\left[R_n^m(C_t)-(D_k^m{)}^T{S}_n^m\right]}^2$

以上是对全连接层码书和索引的优化，而对于卷积层，其方法类似，只是优化函数从式（3.1）变化为
${\min }_{{\left\{D^m\right\}}_{m^{{}^{\prime }}}{\left\{B_{p_k}^m\right\}}_m}{\sum }_{n=1}^N{\sum }_{p_t}{\Vert T_n-{\sum }_{p_k{p}_s}{\sum }_{m=1}^M(D^m{B}_{p_k}^m{)}^T{S}_{n,p_s}^m\Vert }_F^2$ （3.3）
对于具体的优化求解过程，论文的附录中有详细的推导，如果有兴趣的话，可以参考
计算复杂度分析
复杂的分析参见图3.2，分别为计算量与参数存储的计算公式

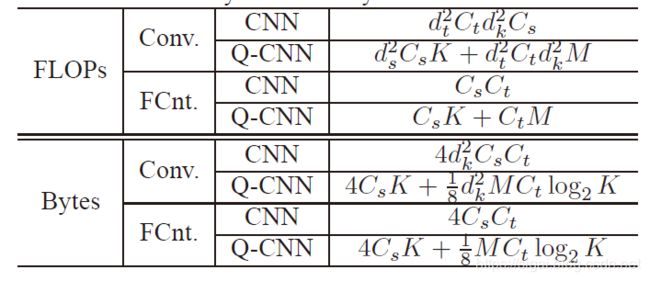
图3.2 计算复杂度分析
式中K是码书中聚类中心的个数，M是子空间的个数，通常$K,M\ll C_s,C_t$

四.实验

作者进行了大量的实验，在MNIST，ILSVRC-12数据集上分别与其他加速压缩方法进行对比，证明了该方法的有效性。
MNIST
实验结果如图4.1所示，通过对比实验，证明了该方法压缩效果与准确率上的优势，在MNIST实验中，作者分别搭建了3层和5层的网络，并设置超参数K=32,$C_s^{{}^{\prime }}=4$,$C_s^{{}^{\prime }}=C_s/M$
图4.1中最后一行表示经过码书和索引调优后的模型，倒数第二行表示调优之前的模型，这个实验同时也表明参数调优确实有助于模型准确率的提高。

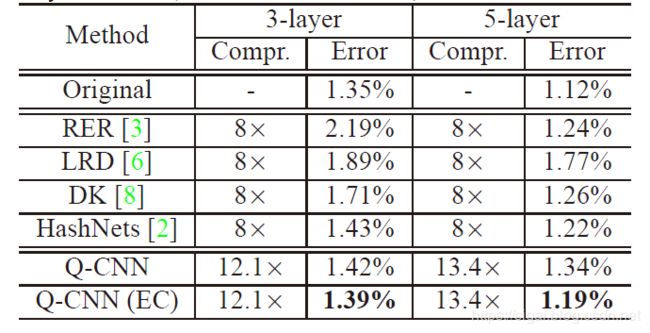
图4.1 MNIST数据集上的对比试验

**ILSVRC-12**

在ILSVRC-12数据集上，作者分别对卷积层、全连接层、以及整体网络的量化进行了实验，进一步证明本文提出的方法的有效性
图4.2为对所有卷积层做量化的结果

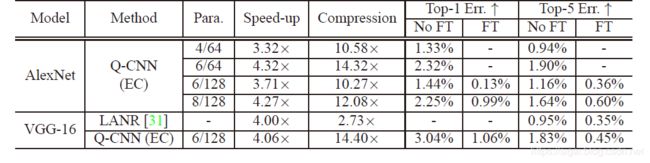
图4.2 ILSVRC-12数据集上对所有卷积层做量化
图4.3为对所有全连接层做量化的结果

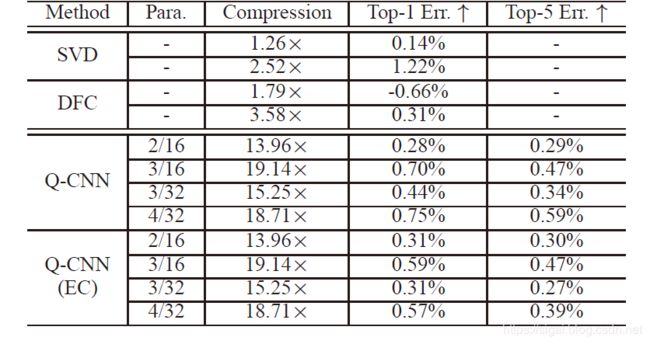
图4.3 ILSVRC-12数据集上对所有全连接层做量化
图4.4为对整个网络做量化的结果，在对整个网路的量化实验中，对于AlexNet，CaffeNet，CNN-S网络，作者设定K=128,$C_s^{{}^{\prime }}=8$；对于VGG16网络，作者设定K=128,$C_s^{{}^{\prime }}=6$

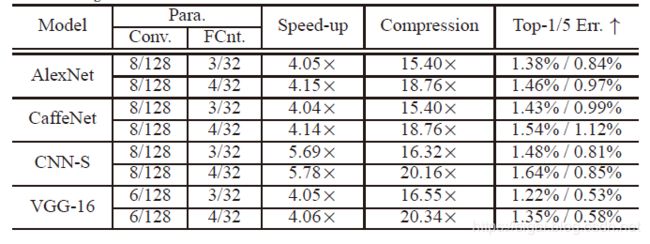
图4.4 ILSVRC-12数据集上对整个网络做量化
移动设备上的结果
图4.5为作者在移动设备上进行实验得到的结果，作者实验的环境是华为Mate7智能手机，1.8G kirin 925 CPU，无GPU加速

图4.5 移动设备上的实际效果

参考文献

[1] W. Chen, J. T. Wilson, S. Tyree, K. Q. Weinberger, and Y. Chen.Compressing neural networks with the hashing trick. In International Conference on Machine Learning (ICML), pages 2285–2294, 2015.

[2] D. C. Ciresan, U.Meier, J.Masci, L.M. Gambardella, and J. Schmidhuber.High-performance neural networks for visual object classification.CoRR, abs/1102.0183, 2011.

[3] M. Denil, B. Shakibi, L. Dinh, M. A. Ranzato, and N. de Freitas.Predicting parameters in deep learning. In Advances in Neural Information Processing Systems (NIPS), pages 2148–2156, 2013.

[4] E. L. Denton, W. Zaremba, J. Bruna, Y. LeCun, and R. Fergus. Exploiting linear structure within convolutional networks for efficient evaluation. In Advances in Neural Information Processing Systems(NIPS), pages 1269–1277, 2014.

[5] J. D. Geoffrey Hinton, Oriol Vinyals. Distilling the knowledge in a neural network. CoRR, abs/1503.02531, 2015.

[6] Y. Gong, L. Liu, M. Yang, and L. D. Bourdev. Compressing deep convolutional networks using vector quantization. CoRR,abs/1412.6115, 2014.

[7] S. Han, H. Mao, and W. J. Dally. Deep compression: Compressing deep neural network with pruning, trained quantization and huffman coding. CoRR, abs/1510.00149, 2015.

[8] M. Jaderberg, A. Vedaldi, and A. Zisserman. Speeding up convolutional neural networks with low rank expansions. In British Machine Vision Conference (BMVC), 2014.

[9] V. Lebedev, Y. Ganin, M. Rakhuba, I. V. Oseledets, and V. S. Lempitsky. Speeding-up convolutional neural networks using fine-tuned cp-decomposition. In International Conference on Learning Representations (ICLR), 2015.

[10] V. Lebedev and V. S. Lempitsky. Fast convnets using group-wise brain damage. CoRR, abs/1506.02515, 2015.

[11] S. Srinivas and R. V. Babu. Data-free parameter pruning for deep neural networks. In British Machine Vision Conference (BMVC),pages 31.1–31.12, 2015.

[12] Z. Yang, M. Moczulski, M. Denil, N. de Freitas, A. J. Smola, L. Song, and Z. Wang. Deep fried convnets. CoRR, abs/1412.7149, 2014.

[13] X. Zhang, J. Zou, K. He, and J. Sun. Accelerating very deep convolutional networks for classification and detection. CoRR, abs/1505.06798, 2015.

[14] X. Zhang, J. Zou, X. Ming, K. He, and J. Sun. Efficient and accurate approximations of nonlinear convolutional networks. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 1984–1992, 2015.