经典算法题目及思路解法总结

一 绪论

1 最大连续子数组：给定一个数组，求它的连续子数组，使得该子数组的和最大
解法：
（1）暴力法
（2）分治法
（3）分析法
（3）动态规划法

2 查找旋转数组的最小值

3 零子数组

4 LCS（最长公共子序列）：两个序列X和Y的公共子序列中，长度最长的那个，定义为X和Y的最长公共子序列
LCS可以描述两段文字之间的“相似度”
解法：
（1）穷举法
（2）动态规划法

5 LCS的应用：最长递增子序列LIS：给定一个长度为N的数组，找出一个最长的单调递增子序列
解法：
（1）使用LCS解LIS
（2）动态规划方法

二 字符串

1 字符串循环左移：给定一个给定一个字符串，要求把S的前k个字符移动到S的尾部，如把字符串“abcdef”前面的2个字符‘a’‘b’移动到字符串的尾部，得到新字符串“cdefab”
解法：
（1）暴力移位法
（2）(X’Y’) = YX

2 字符串的全排列：给定字符串S[0…N-1]，设计算法，枚举S的全排列

3 KMP算法：KMP算法是一种线性时间复杂度的字符串匹配算法，它是对BF（暴力求解）算法的改进

4 DFA和NFA：以当前位置为DFA的状态，以模式串的字符为DFA的转移条件，建立确定有穷自动机

DFA的五要素：
非空有限的状态集合Q
 输入字母表Σ
 转移函数δ
 开始状态S
 结束状态F

5 KMP应用：PowerString问题：给定一个长度为n的字符串S，如果存在一个字符串T，重复若干次T能够得到S，那么，S叫做周期串，T叫做S的一个周期。如：字符串abababab是周期串，abab、ab都是它的周期，其中，ab是它的最小周期。设计一个算法，计算S的最小周期。如果S不存在周期，返回空串

6 求字符串的最长回文子串：该算法的要求，是求字符串中最长的那个回文子串

7 Manacher算法和BM算法

三 数组

1 寻找和为定值的两个数：输入一个数组A[0…N-1]和一个数字Sum，在数组中查找两个数Ai,Aj，使得Ai+Aj=Sum
解法：
（1）暴力法
（2）利用Hash结构求解

2 Hash函数：Hash函数在Hash结构设计中居于核心地位。一个好的Hash函数，能够将数据映射到“杂乱”的位置

三个经典Hash函数：
 dbj2
 sdbm
 MurmurHash

3 分支限界法

4 荷兰国旗问题：现有红、白、蓝三个不同颜色的小球，乱序排列在一起，请重新排列这些小球，使得红白蓝三色的同颜色的球在一起。这个问题之所以叫荷兰国旗，是因为我们可以将红白蓝三色小球想象成条状物，有序排列后正好组成荷兰国旗

5 完美洗牌算法：长度为2n的数组{a1,a2,a3,…,an,b1,b2,b3,…,bn}，经过整理后变成{a1,b1,a2,b2,…,an,bn}，要求时间复杂度O(n)，空间复杂度O(1)

四 树

1 二叉查找树：二叉查找树(二叉搜索树)是满足以下条件的二叉树

 左子树上的所有节点值均小于根节点值

 右子树上的所有节点值均不小于根节点值

 左右子树也满足上述两个条件

二叉树的遍历：

前序遍历：  访问根节点  前序遍历左子树  前序遍历右子树

中序遍历：  中序遍历左子树  访问根节点  中序遍历右子树

后序遍历：  后序遍历左子树  后序遍历右子树  访问根节点

2 平衡二叉树：平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态

3 2-3-4树和B树

五 链表、栈与递归

1 链表相加：给定两个链表，分别表示两个非负整数。它们的数字逆序存储在链表中，且每个结点只存储一个数字，计算两个数的和，并且返回和的链表头指针

2 链表的部分翻转：给定一个链表，翻转该链表从m到n的位置。要求直接翻转而非申请新空间

3 链表划分：给定一个链表和一个值x，将链表划分成两部分，使得划分后小于x的结点在前，大于等于x的结点在后。在这两部分中要保持原链表中的出现顺序

4 排序链表中去重：给定排序的链表，删除重复元素，只保留重复元素第一次出现的结点

5 由LCA引出指针和递归问题：最近公共祖先(Lowest Common Ancestor,LCA)：给定一棵树 T 和两个结点 u 和 v，找出 u 和 v 离根结点最远的公共祖先

6 单链公共结点问题

7 括号匹配：给定字符串，仅由"()[]{}"六个字符组成。设计算法，判断该字符串是否有效

 括号必须以正确的顺序配对，如："()"、"()[]" 是有效的，但"([)]"无效

8 最长括号匹配：给定字符串，仅包含左括号’(‘和右括号’)’，它可能不是括号匹配的，设计算法，找出最长匹配的括号子串，返回该子串的长度。如："(()"：2，"(()())"：6

9 逆波兰表达式RPN

10 直方图矩形面积：给定n个非负整数，表示直方图的方柱的高度，同时，每个方柱的宽度假定都为1；试找出直方图中最大的矩形面积。如：给定高度为：2,1,5,6,2,3，最大面积为10

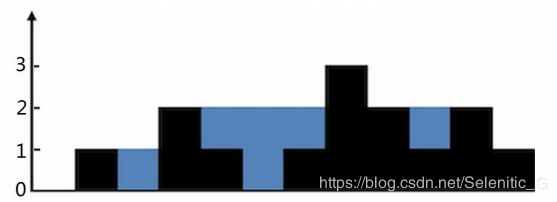
11 另一个直方图例题：收集雨水问题：给定n个非负整数，表示直方图的方柱的高度，同时，每个方柱的宽度假定都为1。若使用这样形状的容器收集雨水，可以盛多少水量

 如输入：0,1,0,2,1,0,1,3,2,1,2,1 返回6

六 图论

1 图的遍历和搜索-广度优先遍历BFS

2 单词变换问题：给定字典和一个起点单词、一个终点单词，每次只能变换一个字母，问从起点单词是否可以到达终点单词？最短多少步？

3 图的遍历和搜索-深度优先搜索DFS

4 八皇后问题：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种解法

5 LCA-Tarjan算法

6 最短路径SPF

7 Floyd算法：Floyd算法又称为插点法，是一种用于寻找给定的加权图中多源点之间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者罗伯特·弗洛伊德命名

8 带负权的最短路径Bellman-ford算法

9 最小生成树MST：最小生成树要求从一个带权无向完全图中选择n－1条边并使这个图仍然连通(也即得到了一棵生成树)，同时还要考虑使树的权最小。最小生成树最著名算法是Prim算法和Kruskal算法

最常见的两种算法：
 Prim算法  Kruskal算法

9 拓扑排序

七 贪心法与动态规划