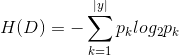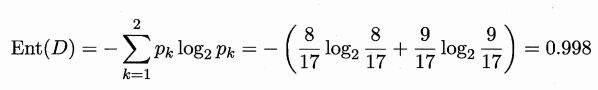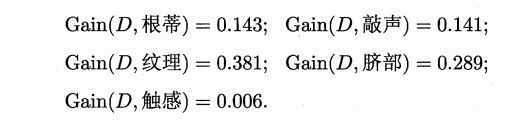独家| 一文读懂决策树的解释和Python代码实现（附Python代码及详细注释）

---

目录

1、决策树基本流程

2、划分选择

3、剪枝处理

决策树Python实现代码：

---

最经典的决策树算法有ID3、C4.5、CART，其中ID3算法是最早被提出的，它可以处理离散属性样本的分类，C4.5和CART算法则可以处理更加复杂的分类问题，本文重点介绍ID3算法。

---

1、决策树基本流程

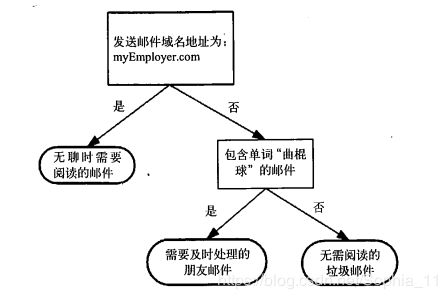
决策树 (decision tree) 是一类常见的机器学习方法。它是对给定的数据集学到一个模型对新示例进行分类的过程。下图所示为一个流程图的决策树，长方形代表判断模块（decision block），椭圆形代表终止模块（terminating block），表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作分支（branch），可以达到另一个判断模块或终止模块。

决策过程是基于树结构来进行决策的。如下图，首先检查邮件域名地址，如果地址为myEmployer.com，则将其分类为“无聊时需要阅读的邮件”。否则，则检查邮件内容里是否包含单词“曲棍球”，如果包含则归类为“需要及时处理的朋友邮件”，如果不包含则归类到“无需阅读的垃圾邮件”

流程图形式的决策树

显然，决策过程的最终结论对应了我们所希望的判定结果，例如"需要阅读"或"不需要阅读”。

决策过程中提出的每个判定问题都是对某个属性的"测试"，如邮件地址域名为？是否包含“曲棍球”？

每个测试的结果或是导出最终结论，或是导出进一步的判定问题，其考虑范国是在上次决策结果的限定范围之内，例如若邮件地址域名不是myEmployer.com之后再判断是否包含“曲棍球”。

一般的，决策树包含一个根节点、若干个内部节点和若干个叶节点。根节点包含样本全集；叶节点对应于决策结果，例如“无聊时需要阅读的邮件”。其他每个结点则对应于一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分到子结点中。

决策树学习基本算法

显然，决策树的生成是一个递归过程.在决策树基本算法中，有三种情形会导致递归返回: (1)当前结点包含的样本全属于同一类别，无需划分; (2)当前属性集为空，或是所有样本在所有属性上取值相同，无法划分; (3)当前结点包含的样本集合为空，不能划分。

---

2、划分选择

决策树算法的关键是如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的"纯度" (purity)越来越高。

（1）信息增益

信息熵

"信息熵" (information entropy)是度量样本集合纯度最常用的一种指标，定义为信息的期望。假定当前样本集合 D 中第 k 类样本所占的比例为

 ,则 D 的信息熵定义为：

                                                                             
H(D)的值越小，则D的纯度越高。

---

信息增益

                                                                 
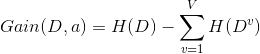
一般而言，信息增益越大，则意味着使周属性 来进行划分所获得的"纯度提升"越大。因此，我们可用信息增益来进行决策树的划分属性选择，信息增益越大，属性划分越好。

---

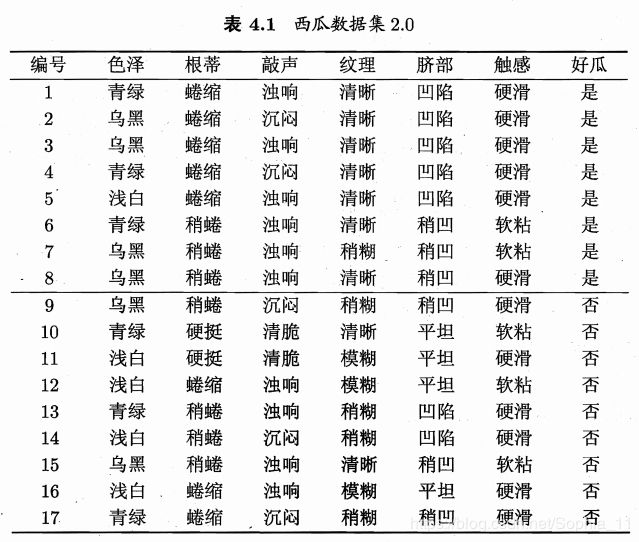
以西瓜书中表 4.1 中的西瓜数据集 2.0 为例，该数据集包含17个训练样例，用以学习一棵能预测设剖开的是不是好瓜的决策树.显然，。

在决策树学习开始时，根结点包含 D 中的所有样例，其中正例占 ，反例占 

信息熵计算为：

我们要计算出当前属性集合{色泽，根蒂，敲声，纹理，脐部，触感}中每个属性的信息增益。以属性"色泽"为例，它有 3 个可能的取值: {青绿，乌黑，浅自}。若使用该属性对 D 进行划分，则可得到 3 个子集，分别记为：D1 (色泽=青绿)， D2 (色泽2=乌黑)， D3 (色泽=浅白)。

子集 D1 包含编号为 {1，4，6，10，13，17} 的 6 个样例，其中正例占 p1=3/6 ，反例占p2=3/6； 

D2 包含编号为 {2，3，7，8， 9，15} 的 6 个样例，其中正例占 p1=4/6 ，反例占p2=2/6； 

D3 包含编号为 {5，11，12，14，16} 的 5 个样例，其中正例占 p1=1/5 ，反例占p2=4/5；

根据信息熵公式可以计算出用“色泽”划分之后所获得的3个分支点的信息熵为：

                                                            

根据信息增益公式计算出属性“色泽”的信息增益为（Ent表示信息熵）：

类似的，可以计算出其他属性的信息增益：

显然，属性"纹理"的信息增益最大，于是它被选为划分属性。图 4.3 给出了基于"纹理"对根结点进行划分的结果，各分支结点所包含的样例子集显示在结点中。

然后，决策树学习算法将对每个分支结点做进一步划分。以图 4.3 中第一个分支结点( "纹理=清晰" )为例，该结点包含的样例集合 D 1 中有编号为 {1, 2, 3, 4, 5, 6, 8, 10, 15} 的 9 个样例，可用属性集合为{色泽，根蒂，敲声，脐部 ，触感}。基于 D1计算出各属性的信息增益：

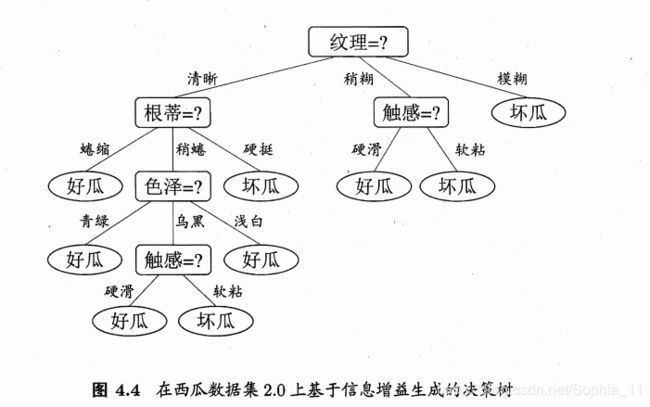
"根蒂"、 "脐部"、 "触感" 3 个属性均取得了最大的信息增益，可任选其中之一作为划分属性.类似的，对每个分支结点进行上述操作，最终得到的决策树如圈 4.4 所示。

---

3、剪枝处理

剪枝 (pruning)是决策树学习算法对付"过拟合"的主要手段。决策树剪枝的基本策略有"预剪枝" (prepruning)和"后剪枝 "(post"
pruning) [Quinlan, 1993]。

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划
分并将当前结点标记为叶结点；

后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

---

决策树Python实现代码：

本篇博文是自己构造的简单数据实验的决策树，后续博文会基于实际的数据集例子运用决策树进行分类使用、

（1）决策树的构造

#!/usr/bin/env python
# -*- coding:utf-8 -*-
from math import log
import operator


def calc_shannon_ent(data_set):
    """计算给定数据集的熵"""
    num_entries = len(data_set)  # 数据集中实例的总数

    # 创建数据字典，键值是最后一列的数值。如果当前键值不存在，则扩展字典并将当前键值加入字典
    # 每个键值都记录了当前类别出现的次数
    label_counts = {}  # 创建数据字典
    for feat_vec in data_set:
        current_label = feat_vec[-1]  # 键值是最后一列的数值，表示类别标签
        # 如果当前键值不存在，则扩展字典并将当前键值加入字典
        if current_label not in label_counts.keys():
            label_counts[current_label] = 0
        label_counts[current_label] += 1

    # 使用所有类标签的发生频率来计算类别出现的概率，并用这个概率来计算熵，统计所有类标签发生的次数
    shannon_ent = 0
    for key in label_counts:
        prob = float(label_counts[key])/num_entries  # 计算类标签的概率
        shannon_ent -= prob * log(prob, 2)  # 计算熵
    return shannon_ent


def create_data_set():
    """创建简单的数据集"""
    data_set = [[1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return data_set, labels


# data_set表示待划分的数据集，axis为划分数据集的特征，value指需要返回的特征的值
def split_data_set(data_set, axis, value):
    """按照给定的特征划分数据集"""
    # Python语言在函数中传递的是列表的引用。在函数内部对对象的修改，将会影响该列表对象的整个生存周期。
    # 为了消除这个不良影响，我们声明一个新列表对象（ret_data_set），用来存储符合要求的值
    ret_data_set = []

    for feat_vec in data_set:
        # print(feat_vec)
        # 将符合特征特征的数据抽取出来
        if feat_vec[axis] == value:
            reduced_feat_vec = feat_vec[: axis]  # 符合特征值的前边的数据（特征位置之前的数据）
            # print(reduced_feat_vec)
            reduced_feat_vec.extend(feat_vec[axis+1:])  # 符合特征值的后边数据（特征位置之后的数据）
            # print(reduced_feat_vec)
            ret_data_set.append(reduced_feat_vec)
    return ret_data_set


def choose_best_feature_to_split(data_set):
    """选择最好的数据集划分"""
    num_features = len(data_set[0])-1  # 数据集特征的个数
    base_entropy = calc_shannon_ent(data_set)  # 计算数据集的熵
    best_info_gain = 0  # 初始化信息最优信息增益
    best_feature = -1  # 初始化最优特征

    # 遍历每个特征
    for i in range(num_features):
        feat_list = [example[i] for example in data_set]  # 提取数据集中i位置特征
        # 将数据集特征转化为独立元素的集合列表。
        # 集合和列表类型相似，不同之处仅在于集合类型中的每个值互不相同
        # 从列表中创建集合是Python语言得到的列表中唯一元素值的最快方法
        unique_vals = set(feat_list)
        new_entropy = 0  # 初始化特征值

        # 遍历给定特征的每个特征值
        for value in unique_vals:
            # 按照给定特征及特征值，划分数据集
            sub_data_set = split_data_set(data_set, i, value)
            prob = len(sub_data_set)/float(len(data_set))  # 计算Dv/D
            new_entropy += prob * calc_shannon_ent(sub_data_set)  # 计算Dv/D*Ent(Dv)并求和
        info_gain = base_entropy - new_entropy  # 计算特征的信息增益

        # 判断最优信息增益，即求最大信息增益
        if info_gain > best_info_gain:
            best_info_gain = info_gain
            best_feature = i
    return best_feature  # 返回最优特征


def majority_cnt(class_list):
    """返回出现次数最多的分类名称"""
    class_count = {}   # 键值为分类名称，值为每个分类名称出现的频率
    # 遍历分类名称列表
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
        class_count[vote] += 1
    # 由大到小排序
    sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
    # 返回出现次数最多的分类名称
    return sorted_class_count[0][0]


# 函数有两个参数：数据集和标签列表。标签列表包含了素有特征的标签
def create_tree(data_set, labels):
    """创建树"""
    class_list = [example[-1] for example in data_set]  # 数据标签列表
    # print('数据标签列表为：', end='')
    # print(class_list)
    # print('class_list[0]为：', end='')
    # print(class_list[0])
    # 第一停止条件是所有的类标签完全相同，则返回该类标签
    # 这里是通过判断第一个键类标签的数量与总数据标签列表长度，如果两者相等，则表明类标签完全相同
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    # 第二个停止条件是使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组
    # 判断data_set[0]的长度为1，说明只剩下标签值，即labels列
    # 因为这里无法简单的返回唯一的类标签，所以这里调用前边的majority_cnt函数挑选出现次数最多的类别作为返回值
    # print('data_set[0]为：', end='')
    # print(data_set[0])
    if len(data_set[0]) == 1:
        return majority_cnt(class_list)
    # 选取最好特征
    best_feat = choose_best_feature_to_split(data_set)
    # print('best_feat为：', end='')
    # print(best_feat)
    # 存储最优特征的label，因为label和最优特征其实就是对应的，best_feat的索引也是特征label的索引
    best_feat_lable = labels[best_feat]
    # print('best_feat_lable为：', end='')
    # print(best_feat_lable)
    my_tree = {best_feat_lable: {}}
    del labels[best_feat]
    # 获取最优特征的属性值
    feat_values = [example[best_feat] for example in data_set]
    # 将最优特征的属性值转换为唯一的元素
    unique_vals = set(feat_values)
    # 遍历最优特征中属性的值。在每个数据集划分上调用函数create_tree()，得到额返回值将会被插入到字典遍历my_tree中
    # 函数终止时，字典中将会嵌套很多叶子节点信息的字典数据
    for value in unique_vals:
        sub_labels = labels[:]  # 使用列表切片复制列表标签类
        my_tree[best_feat_lable][value] = create_tree(split_data_set(data_set, best_feat, value), sub_labels)
    return my_tree


def classify(input_tree, feat_labels, test_vec):
    """使用决策树分类测试数据"""
    first_str = list(input_tree.keys())[0]
    second_dict = input_tree[first_str]
    # 使用index方法查找当前列表中第一个匹配firstStr变量的元素
    feat_index = feat_labels.index(first_str)
    # 遍历整棵树
    for key in second_dict.keys():
        # 如果测试数据的属性值等于Key的值
        if test_vec[feat_index] == key:
            # 判断是否为字典类型，如果是字典类型，则说明不是叶子节点，得需要递归
            # 这里判断得出类别，就是寻找是否是字典类型，如果是字典类型，则不是叶子节点，如果不是字典类型，则说明是叶子结点
            if type(second_dict[key]).__name__ == 'dict':
                class_label = classify(second_dict[key], feat_labels, test_vec)
            else:
                class_label = second_dict[key]
    return class_label


my_data_set, labels = create_data_set()
# 测试数据使用的标签，这里也要注意，为了复制列表labels的副本，
# 我们只能用切片来复制，因为如果使用test_labels=lebels赋值的形式，不会形成新的列表，只是引用而已
test_labels = labels[:]
print('数据集为：', end='')
print(my_data_set)
print('数据集特征标签为：', end='')
print(labels)


# 创建决策树,这里会将labels中的值删除
my_tree = create_tree(my_data_set, labels)
print('树的结构为：', end='')
print(my_tree)

# 测试数据
# my_data_set, labels = create_data_set()
test_classifier = classify(my_tree, test_labels, [1, 1])
print('测试数据结果为：', end='')
print(test_classifier)

运行结果为： 

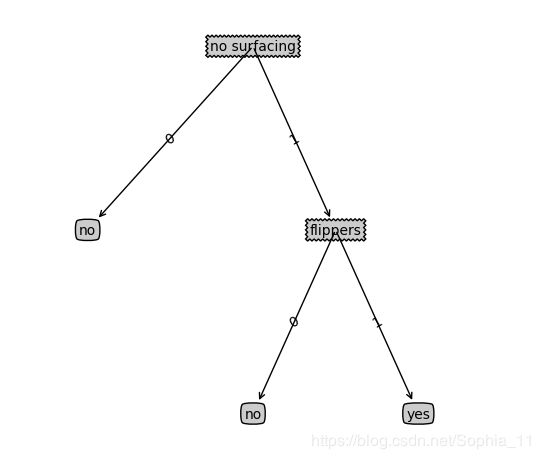
（2）决策树结构的可视化

#!/usr/bin/env python
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
# 设置决策节点和叶节点的边框形状、边距和透明度，以及箭头的形状
decision_node = dict(boxstyle='sawtooth', fc='0.8')  # 决策节点的样式
leaf_node = dict(boxstyle='round4', fc='0.8')  # 叶节点的样式
arrow_args = dict(arrowstyle='<-')  # 箭头的样式


def retrieve_tree(i):
    """存储树的信息"""
    list_of_trees = [{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
                     {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
                     ]
    return list_of_trees[i]


def get_num_leafs(my_tree):
    num_leafs = 0
    first_str = list(my_tree.keys())[0]
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            num_leafs += get_num_leafs(second_dict[key])
        else:
            num_leafs += 1
    return num_leafs


def get_tree_depth(my_tree):
    max_depth = 0
    first_str = list(my_tree.keys())[0]
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            this_depth = 1 + get_tree_depth(second_dict[key])
        else:
            this_depth = 1
        if this_depth > max_depth:
            max_depth = this_depth
    return max_depth


# 该函数需要一个绘图区域
def plot_node(node_txt, center_pt, parent_pt, node_type):
    create_plot.ax1.annotate(node_txt, xy=parent_pt, xycoords='axes fraction',
                             xytext=center_pt, textcoords='axes fraction', va='center',
                             ha='center', bbox=node_type, arrowprops=arrow_args)


# cntr_pt指子节点的坐标，parent_pt指父节点的坐标，txt_string填充的文本消息
def plot_mid_text(cntr_pt, parent_pt, txt_string):
    """在父子节点间填充文本信息"""
    # 填充的位置在父节点和子节点中间位置
    xmid = (parent_pt[0]-cntr_pt[0])/2.0 + cntr_pt[0]
    ymid = (parent_pt[1]-cntr_pt[1])/2.0 + cntr_pt[1]
    create_plot.ax1.text(xmid, ymid, txt_string, va="center", ha="center", rotation=30)


# my_tree指树的信息，patent_pt指父节点的坐标，node_txt指标注的属性信息
def plot_tree(my_tree, parent_pt, node_txt):
    # 获取树的宽度
    num_leafs = get_num_leafs(my_tree)
    # 获取树的深度
    depth = get_tree_depth(my_tree)
    # 第一次划分数据集的类别标签
    first_str = list(my_tree.keys())[0]
    cntr_pt = (plot_tree.x_off + (1.0 + float(num_leafs))/2.0/plot_tree.totalw, plot_tree.y_off)
    # print(cntr_pt, parent_pt)
    # 标记子节点属性值
    plot_mid_text(cntr_pt, parent_pt, node_txt)
    # 子节点标记标签
    plot_node(first_str, cntr_pt, parent_pt, decision_node)
    # 第二个字典
    second_dict = my_tree[first_str]
    # 两个节点之间的距离间隔为：1.0/plot_tree.totald
    plot_tree.y_off = plot_tree.y_off - 1.0/plot_tree.totald
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            plot_tree(second_dict[key], cntr_pt, str(key))
        else:
            plot_tree.x_off = plot_tree.x_off + 1.0/plot_tree.totalw
            print(plot_tree.x_off)
            plot_node(second_dict[key], (plot_tree.x_off, plot_tree.y_off), cntr_pt, leaf_node)
            plot_mid_text((plot_tree.x_off, plot_tree.y_off), cntr_pt, str(key))
    plot_tree.y_off = plot_tree.y_off + 1.0/plot_tree.totald


def create_plot(in_tree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    create_plot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # plot_tree.totalw和plot_tree.totald存储书树的宽度和树的深度
    plot_tree.totalw = get_num_leafs(in_tree)
    plot_tree.totald = get_tree_depth(in_tree)
    # plot_tree.x_off和plot_tree.y_off追踪已经绘制的节点位置，以及放置下一个节点的恰当位置
    plot_tree.x_off = -0.5/plot_tree.totalw
    # print(plot_tree.x_off)
    plot_tree.y_off = 1.0
    plot_tree(in_tree, (0.5, 1.0), '')
    plt.show()

# def create_plot():
#     fig = plt.figure(1, facecolor='white')
#     fig.clf()   # 清空绘图区
#     # 定义一个绘图区域
#     create_plot.ax1 = plt.subplot(111, frameon=False)
#     plot_node('decision_point', (0.5, 0.1), (0.1, 0.5), decision_node)
#     plot_node('leaf_point', (0.8, 0.1), (0.3, 0.8), leaf_node)
#     plt.show()


my_tree = retrieve_tree(0)
create_plot(my_tree)

运行结果为：