优化问题综述(四)有约束最优化算法

最优化问题的三种情况

• 无约束条件：梯度下降法等（前面的文章已经有详细的描述）
• 等式约束条件：解决方法是消元法或者拉格朗日法。
• 不等式约束条件：一般用KKT（Karush Kuhn Tucker）条件对偶求解

等式约束条件下的优化算法

问题的数学描述： minxf(x),s.t.,hi(x)=0,i=1,2,..,I m i n x f ( x ) , s . t . , h i ( x ) = 0 , i = 1 , 2 , . . , I

消元法

根据约束条件消去一些未知数，使得问题变为无约束的优化问题，再用无约束条件的方法求解，但是有时候这样做很困难，甚至是做不到的。

拉格朗日法

拉格朗日函数为 F(x)=f(x)+∑iλihi(x) F ( x ) = f ( x ) + ∑ i λ i h i ( x ) ，对其求解偏导方程 ∂F∂x=0,∂F∂λi=0 ∂ F ∂ x = 0 , ∂ F ∂ λ i = 0 ,如果有 I I 个约束条件，就应该有 I+1 I + 1 个方程。求出的方程组的解就可能是最优化值，将结果带回原方程验证，如果符合要求就可得到解。

拉格朗日乘子法的证明

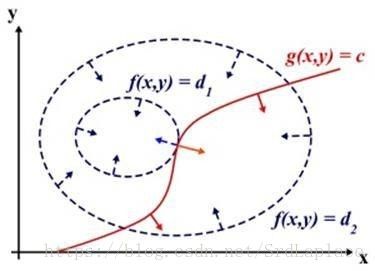
从几何的角度看，如果找到了一个极值点，必然有极值点所在的等高面 f(x)=d f ( x ) = d 与约束曲面 hi(x)=0 h i ( x ) = 0 是相切的。否则，必然还可以沿着约束曲线继续走，找到一个更低的点，这意味着，在极值点：

∇f(x)=−λ∇h(x) ∇ f ( x ) = − λ ∇ h ( x )

因为约束曲面的交线的法线在各个约束曲面法线所组成的超平面上

∇f(x)=−sumiλi∇hi(x) ∇ f ( x ) = − s u m i λ i ∇ h i ( x )

因为拉格朗日函数为 F(x)=f(x)+∑iλihi(x) F ( x ) = f ( x ) + ∑ i λ i h i ( x ) ，那么有

∇xF(x)=∇xf(x)+sumiλi∇xhi(x)=0 ∇ x F ( x ) = ∇ x f ( x ) + s u m i λ i ∇ x h i ( x ) = 0

∇λiF(x)=hi(x)=0 ∇ λ i F ( x ) = h i ( x ) = 0

不等式约束条件下的优化算法

问题的数学描述： minxf(x),s.t.,hk(x)=0,gj(x)<0,k=1,2,..,K,j==1,2,..,J m i n x f ( x ) , s . t . , h k ( x ) = 0 , g j ( x ) < 0 , k = 1 , 2 , . . , K , j == 1 , 2 , . . , J

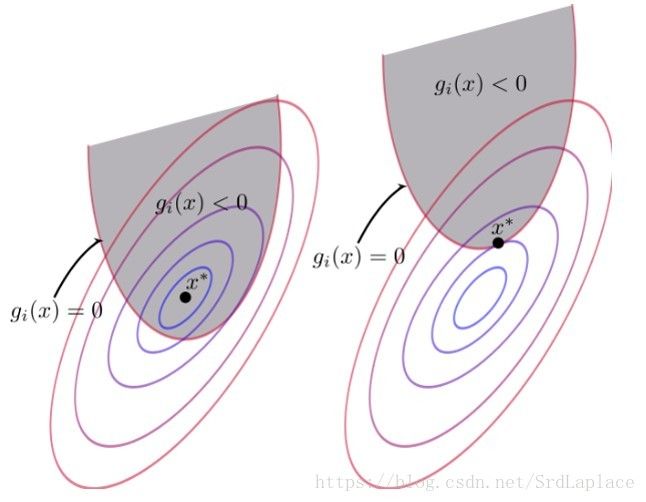
不考虑不等式约束的极小值出现在空间的位置有两种情况：

• 极小值本身就满足不等式约束，此时可以不用理会约束条件，直接求目标函数的极小值；
• 极小值本身不满足不等式约束，此时受约束的极值点所在的等高线必然与 g(x)=0 g ( x ) = 0 曲线相切，否则可以找到更小的值，并且该极小值点关于约束函数的梯度 ∇xg(x) ∇ x g ( x ) 与关于目标函数的梯度 ∇xf(x) ∇ x f ( x ) 方向必定是相反的。
  

KKT条件

拉格朗日函数： L(x,λ,μ)=f(x)+∑kλkhk(x)+∑jλjgj(x),μj≥0 L ( x , λ , μ ) = f ( x ) + ∑ k λ k h k ( x ) + ∑ j λ j g j ( x ) , μ j ≥ 0

由前面的讨论可知

• 如果可行解落在约束边界上： ∇xf(x)=−μ∇xg(x)μj>0 ∇ x f ( x ) = − μ ∇ x g ( x ) μ j > 0
• 如果等式的极小值本身就满足不等式约束：此时约束不起作用 μ=0 μ = 0

KKT条件是说最优值必须满足以下条件：

• ∇xL(x,λ,μ)=0 ∇ x L ( x , λ , μ ) = 0
• μjgj(x)=0 μ j g j ( x ) = 0
• hk(x)=0 h k ( x ) = 0
• gj(x)≤0 g j ( x ) ≤ 0
• μj≥0 μ j ≥ 0

等式约束很容易融入原本最小化问题，现在只考虑问不等式的约束，KKT中不等式约束必须满足：

{gj(x)≤0μj≥0 { g j ( x ) ≤ 0 μ j ≥ 0

那么有 μjgj(x)≤0 μ j g j ( x ) ≤ 0 ，从而有 maxmuL(x,μ)=f(x) m a x m u L ( x , μ ) = f ( x ) ，可知

minxf(x)=minxmaxmuL(x,μ) m i n x f ( x ) = m i n x m a x m u L ( x , μ )

对偶问题： maxmuminxL(x,μ)=maxmuminx[f(x)+μg(x)] m a x m u m i n x L ( x , μ ) = m a x m u m i n x [ f ( x ) + μ g ( x ) ]

μg(x)={0−∞g(x)=0 or μ=0g(x)<0 and μ>0 μ g ( x ) = { 0 g ( x ) = 0   o r   μ = 0 − ∞ g ( x ) < 0   a n d   μ > 0

因此当满足KKT条件时， maxmuminxL(x,μ)=minxf(x) m a x m u m i n x L ( x , μ ) = m i n x f ( x )
KKT条件是个强对偶条件，满足则对偶问题等价于原问题。

对偶问题更一般的描述

原问题的最优解 p∗=minxmaxμL(x,μ)=minxθp(x) p ∗ = m i n x m a x μ L ( x , μ ) = m i n x θ p ( x )
对偶问题的最优解 d∗=maxμminxL(x,μ)=maxμθd(μ) d ∗ = m a x μ m i n x L ( x , μ ) = m a x μ θ d ( μ )
原问题与对偶问题的关系 p∗≥d∗ p ∗ ≥ d ∗
证明： θp(x)=maxμL(x,μ)≥L(x,μ)≥minxL(x,μ)=θd(μ) θ p ( x ) = m a x μ L ( x , μ ) ≥ L ( x , μ ) ≥ m i n x L ( x , μ ) = θ d ( μ )

推论：如果 p∗=d∗ p ∗ = d ∗ ，那么原问题与对偶问题的解 x,μ x , μ 相同

更数学化的描述

L(x,λ,μ)=f(x)+∑kλkhk(x)+sumjμjgj(x),μ≥0 L ( x , λ , μ ) = f ( x ) + ∑ k λ k h k ( x ) + s u m j μ j g j ( x ) , μ ≥ 0

定义域 D×RK×RJ D × R K × R J

G(λ,μ)=infx∈DL(x,λ,μ) G ( λ , μ ) = i n f x ∈ D L ( x , λ , μ )

则原问题的对偶问题为 max(λ,μ)G(λ,μ),μ≥0 m a x ( λ , μ ) G ( λ , μ ) , μ ≥ 0
不论原问题是不是一个凸优化问题，其对偶问题是一个凸优化问题

例子

minxf(x)=x2,s.t.,g(x)=x−5≤0 m i n x f ( x ) = x 2 , s . t . , g ( x ) = x − 5 ≤ 0

解：

L(x,μ)=x2+2μ(x−5) L ( x , μ ) = x 2 + 2 μ ( x − 5 )

∇xL(x,μ)=2x+2μ ∇ x L ( x , μ ) = 2 x + 2 μ

minxmaxμ≥0L(x,μ)=maxμ≥0minxx2+2μ(x−5) m i n x m a x μ ≥ 0 L ( x , μ ) = m a x μ ≥ 0 m i n x x 2 + 2 μ ( x − 5 )

minxx2+2μ(x−5) m i n x x 2 + 2 μ ( x − 5 ) 对应的 x=−μ x = − μ ，值为 −μ2−10μ − μ 2 − 10 μ ，那么 maxμ≥0−μ2−10μ=0 m a x μ ≥ 0 − μ 2 − 10 μ = 0 ，对应的 μ=0 μ = 0