深度学习中常见的优化方法（from SGD to AMSGRAD）和正则化技巧

转载自【泡泡机器人原创专栏】https://mp.weixin.qq.com/s/NmSVXezxsQOZzK8pne3pCw

一．优化方法

这里介绍的优化方法包括:SGD,两种带动量的SGD,AdaGrad,RMSProp,Adadelta,Adam, AMSGRAD，基本涵盖了常用的一些优化算法。先介绍一下优化方法，这里需要注意一下，在深度学习当中，优化的问题是在于鞍点而不是所谓的局部最小值点，在高维空间当中要想在所有维度达到最小，这是一个非常非常小的概率事件。为了避开这些鞍点，出现了许多的优化算法

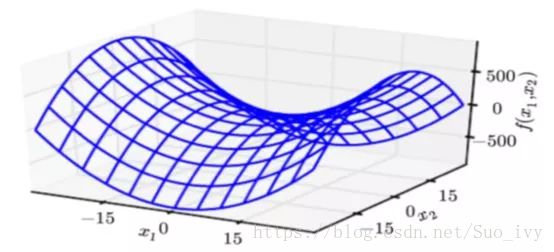
1.基本的梯度下降方法

SGD

首先介绍随机梯度下降法（SGD），随机梯度下降法是梯度下降法的一个特例，梯度下降法是沿着整个样本的梯度下降，但是由于在深度学习中整个样本太大了，比如ImageNet中有上百万张图片，这样计算效率太低。对于批量大小和对梯度估计的准确性的影响，有这样一个规律，批量中的数目越大，对于整个梯度估计得越准确，但是并不是呈线性上升的。小批量虽然比较慢，但是能够提供正则化的效果。

学习率通常设定为前期较快，后期较慢，为了达到这个效果，也有一些设定学习率的方法，比如：每隔一定步数，设定一个衰减，指数衰减，或者每步衰减为原来的几分之一等。

带有动量的SGD

在介绍带动量的SGD之前，首先介绍一下加权指数平滑，这个东西非常简单，但是在后续很多优化算法里面基本都会用到它。虽然随机梯度下降法很有效，但是为了加速它逃离鞍点，可以利用历史信息，其实也就是指数加权平均法，只是加权平均法就是如何结合历史信息和当前信息来优化。指数加权平均法具体公式如下：

如果把这个进行拆开，就会发现它本质是一个加权的平方和，比如这里如果t=5,β=0.1：

这里需要注意的是当第一个数的时候没有历史信息，所以需要引入偏差修正，也就是除以1-β^t  ,随着t的增大，该项会趋于1，所以到了后期基本不会有什么影响。

对于动量的随机梯度下降法，其实就是带有指数加权平均的随机梯度下降法。

这里速度更新部分可能写成v←αv-(1-α)  εg/(1-α)会更加直观一些，从指数加权的角度来理解，那么εg/(1-α)就是历史信息，这里对应的超参数1/(1-α)表示需要加权多少个数据，当α=0.9时，表示以最近10个数的加权，如果等于0.95，则是最近20个数据的加权。

Nesterov动量的随机梯度下降法

这个是受到Nesterov动量的影响，Sutskever等人于2013年提出来的，具体算法过程如下：

这里就是在标准动量的基础之上，先更新一个临时的位置，然后计算该位置上的梯度，再用标准动量法进行估计，也就是在标准的动量法当中加入了一个校正因子。不过这种方法在凸的批量下降中能够加快收敛速度，但是在随机梯度当中效果并不明显。

2.自适应学习率算法

AdaGrad

在之前的算法当中，目标函数自变量的每一个元素在相同时刻都使用同一个学习率来自我迭代，但是这显然是一个不合理的假设，因为有的方向可能快有的可能就比较慢，我们应该个性化差异化的对待每一个变量。AdaGrad算法对每个参数都有一个缩放因子，这个缩放因子反比与历史上的梯度平方值总和的平方根。如果一个变量的损失梯度较大，那么它的下降速度也比较大，如果较小，下降速度也相应减小。具体算法如下：

AdaGrad算法有一个缺点，由于它的速率是一直下降的（分母的值一直在增加），前期下降快，后期下降慢，如果前期就没有找到一个比较好的解，那么他在后期速度非常慢，可能很难找到一个比较好的解。

RMSProp

RMSProp算法是hinton对AdaGrad算法改进，这个算法据说只是hinton在课堂上面提出来的，没有发表相关论文。这个改动其实也很简单，将梯度累计改为移动加权平均，所以也没有什么神奇之处，思路还是比较简单。

当然这里也可以结合Nesterov动量得到结合Nesterov动量的RMSProp算法，具体如下：

Adadelta

该算法不需要设定学习率了，因为它已经不会影响到更新了，这也是该算法的一大优点。该算法在训练前中期速度都比较快，但是在后期会在局部最小值附近波动。

这个算法的基本思想是希望通过一阶的优化算法去近似二阶的优化算法。在1988年LeCun等人曾经提出一种用矩阵对角线元素来近似逆矩阵。如果学过数值分析的同学应该知道，牛顿法用Hessian矩阵替代人工设置的学习率，在梯度下降的时候，可以完美的找出下降方向，不会陷入局部最小值当中，是理想的方法，但是Hessian矩阵的逆在数据很大的情况下根本没办法求。

LeCun等人在2012年又提出了一个更为精确的近似：

这里的E[g_t-w:t]指的是从当前t开始的前w个梯度状态的期望值，E[g_t^2-w:t]指的是从当前t开始的前w个梯度状态的平方的期望值。这里如果求期望的话，非常的麻烦，所以采取了移动平均法来计算。这里作者在论文中也给出了近似的证明：

这里是当f为指数型函数，最后一个近似成立。

对于牛顿法：

由上式可得：

其中：

这里可以用局部的加权指数平滑来替代，即:

这里的RMS表示均方：

可以得到：

Adam

Adam是一个组合了动量法和RMSProp的优化算法，在该算法当中，动量被直接并入了梯度的一阶矩（指数加权）的估计，动量将用于缩放后的梯度，其次Adam包含了偏置修正，修正了从零点初始化的一阶矩和二阶矩的估计。第一个超参数ρ_1负责更新动量项，第二个超参数ρ_2负责更新RMSProp。

AMSGRAD

这是ICML2018年提出来的一个Adam的变体，这篇paper在盲评当中获得极高的分数，最近好像被接受为最佳论文。这篇论文提出了一个通用的边学习率算法框AdaGrad, RMSProp ,Adadelta,Adam等都可以看作是该框架的一种特例。通用的框架如下：

选择两个不同的函数，可以得到不一样的方法，从AdaGrad是两个函数可以看做分别是：

对于Adam而言，函数的选择是基于指数平滑法的：

对应的更新：

作者在论文中证明了Adam在应对一个简单的一维凸函数的优化问题时，都不能得到一个比较好的结果。作者去分析了，发现主要原因在于：

因为这一个是有可能为负的，当其为负的时候，就违背了Adam论文中的Γ_(t+1)半正定假设，因此作者主要就是去改进它，令其始终半正定。作者就想，那么v_(t+1)始终取上一个时刻的和当前估计的最大值就好了这样就可以了。

对于不带修正的AMSGRAD算法可以简单的写成如下：

二．参数初始化

网络参数的初始化能够为网络寻找到一个比较好的起点，不同的初始化方法，可能让给网络的效果千差万别，比如如果参数初始化都是0的话，网络根本学不动。（这里需要注意：在一个网络趋于稳定的情况下，应该是参数正负各占一半，且接近于0，参数的期望应该是0）于是有两种比较简单的初始化方法：将参数初始化为高斯分布或者均匀分布。

2010年有一篇论文，以使得网络中信息更好的流动，每一层输出的方差应该尽量相等的角度出发，推到了一种新的参数初始化方式—Xavier.

首先我们考虑一层的信输入：

根据概率统计的相关知识，我们可以得到：

现在假设权重和输入期望都为0，这里输入期望为0可以用BN来保证（这个方法出来的时候BN还没出来，但是当时只是这样假设的），权重的期望为0是我们要得到的结果。上式可以写为:

现在假定n个输入都独立同分布，可以得到：

根据输入和输出同分布则有：

这里n_i表示第i层的参数个数。

同理对于方向传播过程进行同样的推到，可以得到：

但是在实际应用中，输入和输出往往不等，于是取了一个折中:

对于均匀分布而言，在均匀分布区间[-a,a]上的方差为：

两者带入，可以得均匀分布区间为：

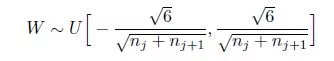
三．正则化

我之前一直不知道正则化为什么能够提高泛化性能，直到后来我上了计算机视觉才知道，所谓的正则化就是先验，只要这个先验是正确的，那么他肯定能够提高泛化性能。一般的机器学习都是有两部分组成，预测+先验，也就是预测项和正则化项。正则化是机器学习中通过显式的控制模型复杂度来避免模型过拟合、确保泛化能力的一种有效方式。常见的正则化有：L1，L2等。在深度学习中主要有Dropout和BN两种，BN（批归一化）已经基本取代dropout的趋势，最近何凯明团队又提出了一个GN（组归一化）。

L1正则化就是L1范数，L2正则化是参数的平方和(这里需要注意L2范数是参数平方和的平方根)，L1正则化会让参数变得稀疏，L2正则化会让参数变得平滑。

Dropout是2012年在ImageNet大赛上面提出来的一种方法，就是随机失活，让每一个节点的输出随机的置0，这样相当于我们训练了很多个子网络，然后在测试的输出就是子网络结果的一个综合输出。Dropout的实现其实也比较简单，直接用random产生数据，然后与keep_prob做比较，大的为true，小的为false，其实就是0和1，然后让这个矩阵与输出点乘，最后再将这个输出除以keep_prob，这里除以keep_prob是为了使得不改变输出期望。

BN，这个可以说是深度学习里面一个非常重大的突破，为什么BN会有效果？google的两位研究员也做了分析解释，首先在机器学习当中有一个非常重要的假设：目标空间（目标数据）和源空间（训练数据）要属于同样的分布，这样我们学到的东西才能用嘛，这个是比较好理解的。如果两者分布不一致，那么就会出现新的机器学习方法，比如迁移学习。Covariate Shift是两者不一致的一个分支，它具体而言就是说两者的条件概率相同，但是边缘概率却不同，那么对于深度学习而言，确实是这样的，不同的层经过各种线性非线性操作之后，分布肯定发生了变化，但是他们却都表示同样的一个label，这也就是Covariate Shift。那么如何做，其实也就是统计学里面非常简单的，减均值，除以方差，这样其实保证均值和方差是相等的，然后再学习一个尺度的变换和偏移，这里为什么还要再加这个尺度的变换和偏移，是因为简单的标准化容易让他们失去一些需要表达的内容，以简单的sigmoid函数为例，标准化之后它基本就丧失了非线性部分，仅剩下线性部分，所以还需要再加参数，让他们自动的去学习。

这里我看了一些知乎上面的一些讨论，觉得很有道理，其实上面的Covariate Shift是作者弄的一些包装纸，本质上BN有效的原因是因为规范化了输入，这样可以把各个层的尺度都统一起来，解决了梯度的问题。BN的位置一般是在卷积之后，激活函数之前。

那么在测试的时候，这个均值和方差怎么确定呢？这个比较简单，我们可以根据统计学的规律来求，均值为所有批次均值的期望，方差也是所有批次的方差的期望，具体公式如下：

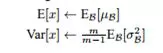
带入即可，得到下式：

RBN是BN的作者在2017年发表的新的一篇文章，这篇文章是对BN的一个改进，因为BN在训练和测试的均值方差其实是不一样的，同时每个batch比较小的时候，均值和方差估计就不准了，于是作者对均值和方差做了一个修正，具体的方法如下：

组归一化(GN)是何凯明团队最近提出来的一种归一化算法，其思想还是BN的思想，不过是从channel上面进行操作，计算channel上每个组的均值和方差，所以和bathsize没有关系，那么受到batchsize的影响也就不大了，下图展示了几种Norm的关系。

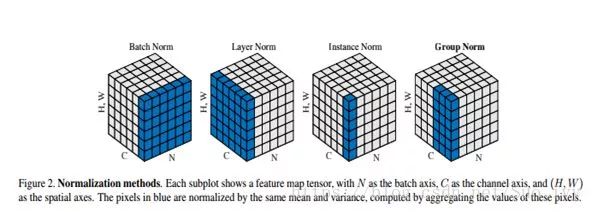
代码也很简单：

参考资料：

【1】吴恩达.deeplearning课程http://mooc.study.163.com/smartSpec/detail/1001319001.htm

【2】Ian Goodfellow,Yoshua Bengo,Aaron Courville.《deep learning》(中文版)

【3】李沐.动手学深度学习第一季  http://zh.gluon.ai/

【4】魏秀参.《解析卷积神经网络》

【5】新智元.【深度干货】2017年深度学习优化算法研究亮点最新综述（附slide下载）

【6】Matthew D. Zeiler.ADADELTA: AN ADAPTIVE LEARNING RATE METHOD

【7】Sergey Ioffe,Christian Szegedy.Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

【8】Sergey Ioffe.Batch Renormalization: Towards Reducing Minibatch Dependence in Batch NormalizedModels

【9】Yuxin Wu,Kaiming He.Group Normalization

【10】Sashank J. Reddi, Satyen Kale & Sanjiv Kumar.ON THE CONVERGENCE OF ADAM AND BEYOND

【11】Xavier Glorot,Yoshua Bengio.Understanding the difficulty of training deep feedforward neural networks