《算法图解》学习笔记（六）：图和广度优先搜索（附代码）

python学习之路 - 从入门到精通到大师

一、图简介

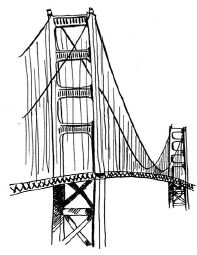
假设你居住在旧金山，要从双子峰前往金门大桥。你想乘公交车前往，并希望换乘最少。可乘坐的公交车如下：

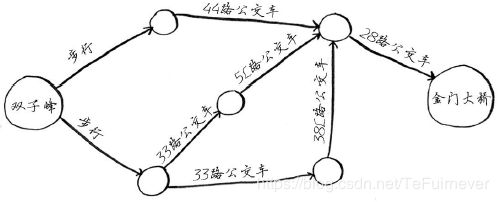
为找出换乘最少的乘车路线，你将使用什么样的算法？一步就能到达金门大桥吗？下面突出了所有一步就能到达的地方。

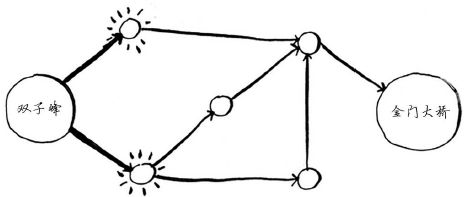
金门大桥未突出，因此一步无法到达那里。两步能吗？

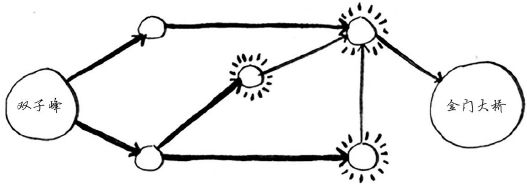
金门大桥也未突出，因此两步也到不了。三步呢？

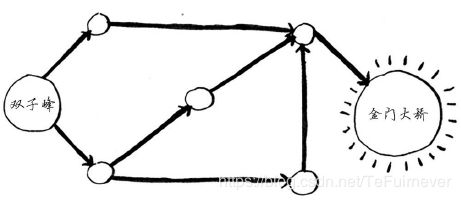
金门大桥突出了！因此从双子峰出发，可沿下面的路线三步到达金门大桥。

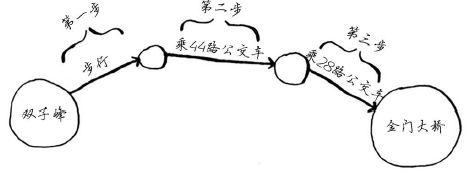
还有其他前往金门大桥的路线，但它们更远（需要四步）。这个算法发现，前往金门大桥的最短路径需要三步。这种问题被称为 最短路径问题（shorterst-path problem）。你经常要找出最短路径，这可能是前往朋友家的最短路径，也可能是国际象棋中把对方将死的最少步数。解决最短路径问题的算法被称为广度优先搜索。

要确定如何从双子峰前往金门大桥，需要两个步骤。

1. 使用图来建立问题模型。
2. 使用广度优先搜索解决问题。

二、图是什么

图模拟一组连接。

例如，假设你与朋友玩牌，并要模拟谁欠谁钱，可像下面这样指出 Alex 欠 Rama 钱。

完整的欠钱图可能类似于下面这样。

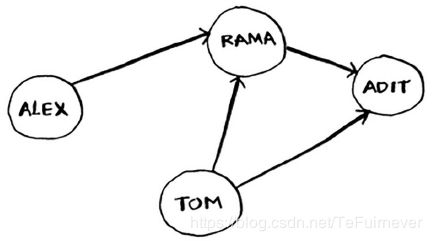
Alex 欠 Rama 钱，Tom 欠 Adit 钱，等等。图由节点（node）和边（edge）组成。

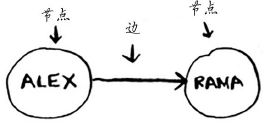
就这么简单！图由节点和边组成。一个节点可能与众多节点直接相连，这些节点被称为邻居。在前面的欠钱图中，Rama 是 Alex 的邻居。Adit 不是 Alex 的邻居，因为他们不直接相连。但 Adit 既是 Rama 的邻居，又是 Tom 的邻居。图用于模拟不同的东西是如何相连的。

三、广度优先搜索

介绍第一种图算法——广度优先搜索（breadth-first search，BFS）。在第1章我们介绍了一种查找算法——二分查找（《算法图解》学习笔记（一）：二分查找（附代码））。广度优先搜索是一种用于图的查找算法，可帮助回答两类问题。

• 第一类问题：从节点A出发，有前往节点B的路径吗？
• 第二类问题：从节点A出发，前往节点B的哪条路径最短？

广度优先搜索让你能够找出两样东西之间的最短距离，不过最短距离的含义有很多！使用广度优先搜索可以：

• 编写国际跳棋AI，计算最少走多少步就可获胜；
• 编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将READED改为READER需要编辑一个地方；
• 根据你的人际关系网络找到关系最近的医生。

还有很多，这里就不一一列举了。

前面计算从双子峰前往金门大桥的最短路径时，你使用过广度优先搜索。这个问题属于第二类问题：哪条路径最短？下面来详细地研究这个算法，你将使用它来回答第一类问题：有路径吗？

假设你经营着一个芒果农场，需要寻找芒果销售商，以便将芒果卖给他。在Facebook，你与芒果销售商有联系吗？为此，你可在朋友中查找。

这种查找很简单。首先，创建一个朋友名单。

然后，依次检查名单中的每个人，看看他是否是芒果销售商。

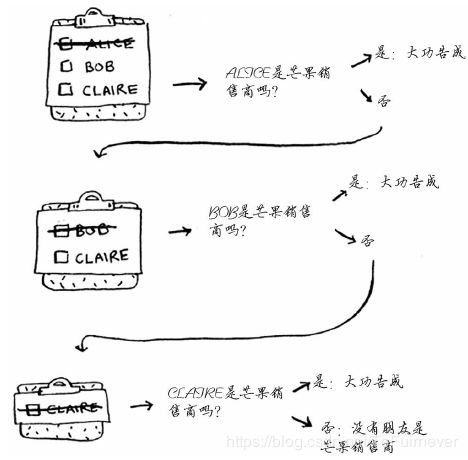
假设你没有朋友是芒果销售商，那么你就必须在朋友的朋友中查找。

检查名单中的每个人时，你都将其朋友加入名单。

这样一来，你不仅在朋友中查找，还在朋友的朋友中查找。别忘了，你的目标是在你的人际关系网中找到一位芒果销售商。因此，如果 Alice 不是芒果销售商，就将其朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直到找到芒果销售商。这就是 广度优先搜索算法。

1）查找最短路径

再说一次，广度优先搜索可回答两类问题。

• 第一类问题：从节点A出发，有前往节点B的路径吗？（在你的人际关系网中，有芒果销售商吗？）
• 第二类问题：从节点A出发，前往节点B的哪条路径最短？（哪个芒果销售商与你的关系最近？）

刚才你看到了如何回答第一类问题，下面来尝试回答第二类问题——谁是关系最近的芒果销售商。例如，朋友是一度关系，朋友的朋友是二度关系。

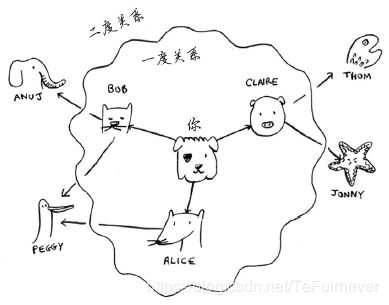
在你看来，一度关系胜过二度关系，二度关系胜过三度关系，以此类推。因此，你应先在一度关系中搜索，确定其中没有芒果销售商后，才在二度关系中搜索。广度优先搜索就是这样做的！在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。顺便问一句：将先检查 Claire 还是 Anuj 呢？Claire 是一度关系，而Anuj是二度关系，因此将先检查 Claire，后检查 Anuj。

你也可以这样看，一度关系在二度关系之前加入查找名单。

你按顺序依次检查名单中的每个人，看看他是否是芒果销售商。这将先在一度关系中查找，再在二度关系中查找，因此找到的是关系最近的芒果销售商。广度优先搜索不仅查找从A到B的路径，而且找到的是最短的路径。

注意，只有按添加顺序查找时，才能实现这样的目的。换句话说，如果 Claire 先于 Anuj 加入名单，就需要先检查Claire，再检查 Anuj。如果 Claire 和 Anuj 都是芒果销售商，而你先检查 Anuj 再检查 Claire，结果将如何呢？找到的芒果销售商并非是与你关系最近的，因为 Anuj 是你朋友的朋友，而 Claire 是你的朋友。因此，你需要按添加顺序进行检查。有一个可实现这种目的的数据结构，那就是 队列（queue）。

2）队列

队列的工作原理与现实生活中的队列完全相同。

假设你与朋友一起在公交车站排队，如果你排在他前面，你将先上车。队列的工作原理与此相同。队列类似于栈，你不能随机地访问队列中的元素。队列只支持两种操作：入队和出队。

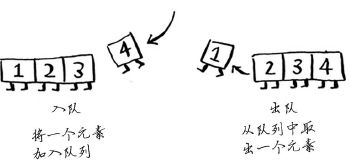
如果你将两个元素加入队列，先加入的元素将在后加入的元素之前出队。因此，你可使用队列来表示查找名单！这样，先加入的人将先出队并先被检查。

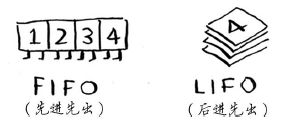
队列是一种 先进先出（First In First Out，FIFO） 的数据结构，而栈是一种 后进先出（Last InFirst Out，LIFO） 的数据结构。

四、实现图

首先，需要使用代码来实现图。图由多个节点组成。

每个节点都与邻近节点相连，如果表示类似于“你→Bob”这样的关系呢？好在你知道的一种结构让你能够表示这种关系，它就是哈希表（《算法图解》学习笔记（五）：哈希表，小名散列表（附代码））！

记住，哈希表让你能够将键映射到值。在这里，你要将节点映射到其所有邻居。

表示这种映射关系的Python代码如下。

graph = {}
graph["you"] = ["alice", "bob", "claire"]

注意，“你”被映射到了一个数组，因此 graph [“you”] 是一个数组，其中包含了“你”的所有邻居。

图不过是一系列的节点和边，因此在Python中，只需使用上述代码就可表示一个图。那像下面这样更大的图呢？

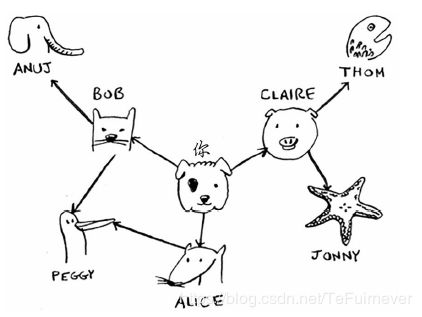
表示它的Python代码如下。

graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

顺便问一句：键—值对的添加顺序重要吗？换言之，如果你这样编写代码：

graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []

而不是这样编写代码：

graph["anuj"] = []
graph["claire"] = ["thom", "jonny"]

对结果有影响吗？

只要回顾一下前一章介绍的内容（《算法图解》学习笔记（五）：哈希表，小名散列表（附代码）），你就知道没影响。哈希表是无序的，因此添加键—值对的顺序无关紧要。

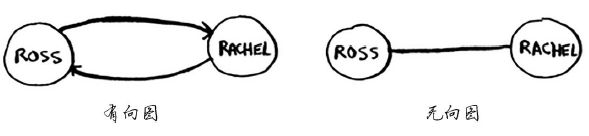
Anuj、Peggy、Thom 和 Jonny 都没有邻居，这是因为虽然有指向他们的箭头，但没有从他们出发指向其他人的箭头。这被称为 有向图（directed graph），其中的关系是单向的。因此，Anuj 是 Bob 的邻居，但 Bob 不是 Anuj 的邻居。无向图（undirected graph） 没有箭头，直接相连的节点互为邻居。例如，下面两个图是等价的。

五、实现算法

先概述一下这种算法的工作原理。

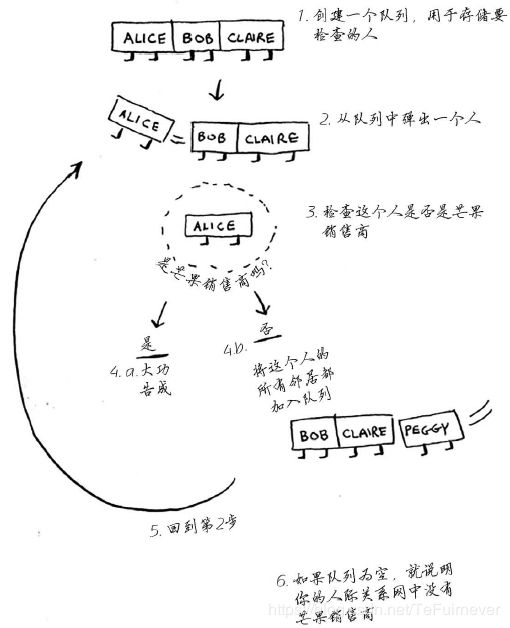
首先，创建一个队列。在Python中，可使用函数deque来创建一个双端队列。

from collections import deque
search_queue = deque() # 创建一个队列
search_queue += graph["you"] # 将你的邻居都加入到这个搜索队列中

别忘了，graph [“you”] 是一个数组，其中包含你的所有邻居，如 [“alice”, “bob”, “claire”]。这些邻居都将加入到搜索队列中。

下面来看看其他的代码。

while search_queue: # 只要队列不为空，
	person = search_queue.popleft() # 就取出其中的第一个人
	if person_is_seller(person): # 检查这个人是否是芒果销售商
		print(person + " is a mango seller!") # 是芒果销售商
		return True
	else:
		search_queue += graph[person] # 不是芒果销售商。将这个人的朋友都加入搜索队列
return False # 如果到达了这里，就说明队列中没人是芒果销售商

最后，你还需编写函数 person_is_seller，判断一个人是不是芒果销售商，如下所示。

def person_is_seller(name):
	return name[-1] == 'm'

这个函数检查人的姓名是否以m结尾：如果是，他就是芒果销售商。这种判断方法有点搞笑，但就这个示例而言是可行的。下面来看看广度优先搜索的执行过程。

这个算法将不断执行，直到满足以下条件之一：

• 找到一位芒果销售商；
• 队列变成空的，这意味着你的人际关系网中没有芒果销售商。

Peggy 既是 Alice 的朋友又是 Bob 的朋友，因此她将被加入队列两次：一次是在添加 Alice 的朋友时，另一次是在添加 Bob 的朋友时。因此，搜索队列将包含两个 Peggy。

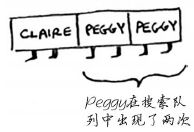
但你只需检查Peggy一次，看她是不是芒果销售商。如果你检查两次，就做了无用功。因此，检查完一个人后，应将其标记为已检查，且不再检查他。如果不这样做，就可能会导致无限循环。假设你的人际关系网类似于下面这样。

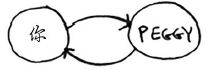
一开始，搜索队列包含你的所有邻居。

现在你检查Peggy。她不是芒果销售商，因此你将其所有邻居都加入搜索队列。

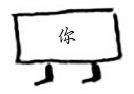
接下来，你检查自己。你不是芒果销售商，因此你将你的所有邻居都加入搜索队列。

以此类推。这将形成无限循环，因为搜索队列将在包含你和包含Peggy之间反复切换。

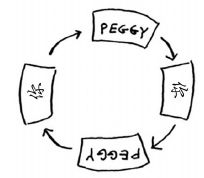
检查一个人之前，要确认之前没检查过他，这很重要。为此，你可使用一个列表来记录检查过的人。

考虑到这一点后，广度优先搜索的最终代码如下。

def search(name):
	search_queue = deque()
	search_queue += graph[name]
	searched = [] # 这个数组用于记录检查过的人
	while search_queue:
		person = search_queue.popleft()
		if not person in searched: # 仅当这个人没检查过时才检查
			if person_is_seller(person):
				print person + " is a mango seller!"
				return True
		else:
			search_queue += graph[person]
			searched.append(person) # 将这个人标记为检查过
	return False
	
search("you")

请尝试运行这些代码，看看其输出是否符合预期。你也许应该将函数 person_is_seller 改为更有意义的名称。

python版本代码如下：

from collections import deque

def person_is_seller(name):
      return name[-1] == 'm'

graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

def search(name):
    search_queue = deque()
    search_queue += graph[name]
    #这个数组是如何跟踪你以前搜索过的人的
    searched = []
    while search_queue:
        person = search_queue.popleft()
        #只有在你还没搜过这个人的时候才搜
        if person not in searched:
            if person_is_seller(person):
                print(person + " is a mango seller!")
                return True
            else:
                search_queue += graph[person]
                #将此人标记为已搜索
                searched.append(person)
    return False

search("you")

c++版本代码如下：

#include 
#include 
#include 
#include 
#include 
#include 

using std::cout;
using std::endl;

bool is_seller(const std::string& name) {
    return name.back() == 'm';
}

template <typename T>
bool search(const T& name, const std::unordered_map<T, std::vector<T>>& graph) {
    std::queue<T> search_queue;
    std::unordered_set<T> searched;

    // add all friends to search queue
    for (auto friend_name : graph.find(name) -> second) {
        search_queue.push(friend_name);
    }

    while (!search_queue.empty()) {
        T& person = search_queue.front();
        search_queue.pop();

        // only search this person if you haven't already searched them.
        if (searched.find(person) == searched.end()) {
            if (is_seller(person)) {
                cout << person << " is a mango seller!" << endl;
                return true;
            }
            std::vector<T> friend_list = graph.find(person) -> second;
            
            // add all friends of a person to search queue
            for (T friend_name : friend_list) {
                search_queue.push(friend_name);
            }

            // mark this person as searched
            searched.insert(person);
        }
    }

    return false;
}

int main() {
    std::unordered_map<std::string, std::vector<std::string>> graph;
    graph.insert({"you", {"alice", "bob", "claire"}});
    graph.insert({"bob", {"anuj", "peggy"}});
    graph.insert({"alice", {"peggy"}});
    graph.insert({"claire", {"thom", "jonny"}});
    graph.insert({"anuj", {}});
    graph.insert({"peggy", {}});
    graph.insert({"thom", {}});
    graph.insert({"jonny", {}});

    std::string name = "you";
    bool result = search(name, graph);
    cout << "Found mango seller: " << result << endl;
}

六、运行时间

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。

你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点数，E为边数。

七、小结

• 广度优先搜索指出是否有从A到B的路径。
• 如果有，广度优先搜索将找出最短路径。
• 面临类似于寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来解决问题。
• 有向图中的边为箭头，箭头的方向指定了关系的方向，例如，rama→adit表示rama欠adit钱。
• 无向图中的边不带箭头，其中的关系是双向的，例如，ross - rachel表示“ross与rachel约会，而rachel也与ross约会”。
• 队列是先进先出（FIFO）的。
• 栈是后进先出（LIFO）的。
• 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列。
• 对于检查过的人，务必不要再去检查，否则可能导致无限循环。

参考文章

• 《算法图解》