斯坦福机器学习第五周（如何训练神经网络）

上一周Andrew Ng 介绍如何应用神经网络来识别手写体时，其网络已经是训练好的。也就是说整个网络的参数 Θ(i) 是已知的，而这一周的主要内容就是如何来训练一个神经网络，换句话说就是如何找到参数 Θ .

当然，采用的方法依旧是梯度下降或者fminunc等方法。但是使用这些方法的前提是给出代价函数 J(Θ)，以及代价函数关于每参数θ的梯度，即∂∂θlijJ(Θ)

1.Cost function

J(Θ)=−1m∑i=1m∑k=1K[y(i)klog((hΘ(x(i)))k)+(1−y(i)k)log(1−(hΘ(x(i)))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2

关于代价函数的解释，戳此处

2.Fitting parameters

上面说到，fitting parameter主要用到的就是梯度下降，而运用梯度下降就要先计算梯度。所以训练神经网络的主要问题首先就变成了求梯度。

而求梯度主要的高效算法就是反向传播算法(back propagation)

下面直接给出需要用到的公式：（推导过程戳此处）

∂J∂WlδLδl=δl+1⋅(al)T⋯⋯⋯(1)=aL−y⋯⋯⋯(2)=(Wl)Tδl+1.∗f′(zl)⋯(3)

这时可以发现，进行反向传播前，先要进行正向传播，计算出每一个神经元的激活值。

下面给出正向传播的计算公式：

z(j)=Θ(j−1)a(j−1)……(4)a(j)=g(z(j)),setting a(j)0=1……(5)hΘ(x)=a(j)=g(z(j))……(6)

正向传播：

反向传播：

两者合在一起的计算步骤：

注：公式(1)中计算的不包括regular term项的偏导数，所以 Δl 中未包含regular term对参数的偏导，而最后的 Dl 才是真正代价函数关于参数的梯度。

此时所有的梯度都已经计算完毕了，也就意味着可以用梯度下降或者fminuc等方法来训练网络了。但是，为了在使用Matlab编程的时传递参数更加方便，Andrew Ng 接下来就讲了一些技巧。

2.1 Unrolling parameters

例如，代价函数返回梯度以及传参的时候。由于网络中每一层的参数都是一个矩阵，就要传递多个参数。但是，如果进行unrolling parameters之后，就变成一个参数了，等需要的时候再还原即可。

[jval,gradient]=costFunction(theta);

举个例子：

>> A = [1 2 3 ;4 5 6]
A =

     1     2     3
     4     5     6
>> B = [7 8;9 10]
B =

     7     8
     9    10

C = [A(:);B(:)]%%  这一步就叫 unrolling
C =
     1
     4
     2
     5
     3
     6
     7
     9
     8
    10

%下面进行还原
>> a=reshape(C(1:6),size(A))% 或者a=reshape(C(1:6),2,3)

a =

     1     2     3
     4     5     6

>> b = reshape(C(7:10),2,2)%其中C(7:10)表示取后面第7到第10个元素

b =

     7     8
     9    10

关于reshape的用法戳此处

2.2 Gradient Checking

由于反向传播算法在应用的时候稍微有点复杂，所以很容易就会出现你不易察觉的bug。虽然此时你的代价函数在每次迭代的时候都在减小，但是最终相对于最优的参数来说，这个代价函数依旧显得很大。因此，我们就需要一种方法来检测反向传播算法是否出现错误，由此引出了梯度检验（gradient checking）.

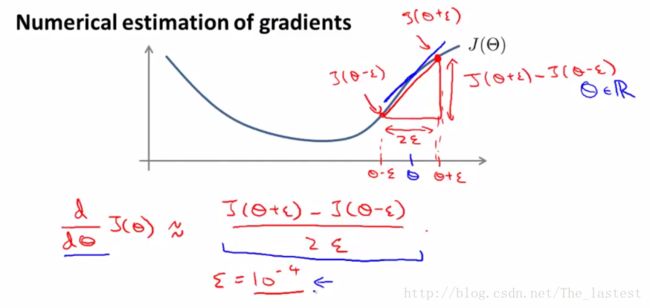
梯度检验的做法就是：手动用公式计算出梯度，然后同反向传播计算出来的梯度进行比较，如果两者相差特别小，则认为反向传播运行正常。下图就是通过导数定义计算出来的梯度。

A small value for ϵ (epsilon) such as ϵ=10−4 , guarantees that the math works out properly. If the value for ϵ is too small, we can end up with numerical problems.

一般来讲 ϵ 不宜过大，这样计算出来的结果就更接近于真是的导数值；但也不宜非常非常小。Andrew Ng 通常取 ϵ=10−4

Gradient checking will assure that our backpropagation works as intended. We can approximate the derivative of our cost function with:

∂∂ΘJ(Θ)≈J(Θ+ϵ)−J(Θ−ϵ)2ϵ

With multiple theta matrices, we can approximate the derivative with respect to Θj as follows:

∂∂ΘjJ(Θ)≈J(Θ1,…,Θj+ϵ,…,Θn)−J(Θ1,…,Θj−ϵ,…,Θn)2ϵ

Matlab\Octave中的实现方法。

值得注意的是，梯度检验只进行一次即可。换句话说就是在训练网络之前，用一组数据测试一下即可。

2.3 Random initialization

同之前的回归模型一样，神经网络在训练的时候也要进行参数的初始化。通常对出参数初始化的处理也是有一定技巧的，或者说有值得注意的地方。在神经网络的训练中，对于参数的初始化采用的是随机初始化的方法。

3.Training network

经过第二步得到代价函数关于所有参数的梯度之后，我们就可以用梯度下降或者matlab中的fminuc算法来进行训练了。

具体实例，戳此处