详解全排列算法
简介
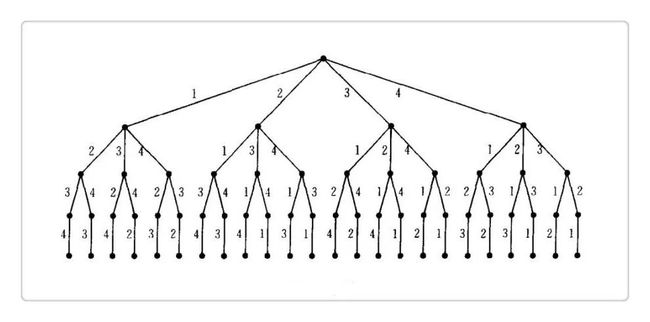
给定 {1, 2, 3, , , n},其全排列为 n! 个,这是最基础的高中组合数学知识。我们以 n=4 为例,其全部排列如下图(以字典序树形式来呈现):
我们很容易想到用递归来求出它的所有全排列。
仔细观察上图,
以 1 开头,下面跟着 {2, 3, 4} 的全排列;
以 2 开头,下面跟着 {1, 3, 4} 的全排列;
以 3 开头,下面跟着 {1, 2, 4} 的全排列;
以 4 开头,下面跟着 {1, 2, 3} 的全排列。
代码如下:
/**
*
* author : 刘毅(Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
using namespace std;
void FullPermutation(int array[], int left, int right)
{
if (left == right)
{
for (int i = 0; i < 4; i++)
cout << array[i] << " ";
cout << endl;
}
else
{
for (int i = left; i <= right; i++)
{
swap(array[i], array[left]);
FullPermutation(array, left + 1, right);
swap(array[i], array[left]);
}
}
}
int main()
{
int array[4] = { 1,2,3,4 };
FullPermutation(array, 0, 3);
return 0;
}
运行如下:
咦~ 递归写出的全排列有点不完美,它并不严格遵循字典序。但是熟悉 C++ 的朋友肯定知道另一种更简单,更完美的全排列方法。
定义于文件
1、next_permutation,对于当前的排列,如果在字典序中还存在下一个排列,返回真,并且把当前排列调整为下一个排列;如果不存在,就把当前排列调整为字典序中的第一个排列(即递增排列),返回假。
2、prev_permutation,对于当前的排列,如果在字典序中还存在上一个排列,返回真,并且把当前排列调整为上一个排列;如果不存在,就把当前排列调整为字典序中的最后一个排列(即递减排列),返回假。
/**
*
* author : 刘毅(Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
using namespace std;
void FullPermutation(int array[])
{
do
{
for (int i = 0; i < 4; i++)
cout << array[i] << " ";
cout << endl;
} while (next_permutation(array, array + 4));
}
int main()
{
int array[4] = { 1,2,3,4 };
FullPermutation(array);
return 0;
}
运行截图省略。输出结果正好符合字典序。
那这个 “轮子” 是怎么做的呢?(摘自侯捷的《STL 源码剖析》)
1、next_permutation,首先,从最尾端开始往前寻找两个相邻元素,令第一元素为*i,第二元素为*ii,且满足*i < *ii,找到这样一组相邻元素后,再从最尾端开始往前检验,找出第一个大于*i的元素,令为*j,将 i,j 元素对调,再将 ii 之后的所有元素颠倒排列,此即所求之 “下一个” 排列组合。
2、prev_permutation,首先,从最尾端开始往前寻找两个相邻元素,令第一元素为*i,第二元素为*ii,且满足*i > *ii,找到这样一组相邻元素后,再从最尾端开始往前检验,找出第一个小于*i的元素,令为*j,将 i,j 元素对调,再将 ii 之后的所有元素颠倒排列,此即所求之 “上一个” 排列组合。
代码如下:
bool next_permutation(int * first, int * last)
{
if (first == last) return false; // 空区间
int * i = first;
++i;
if (i == last) return false; // 只有一个元素
i = last;
--i;
for (;;)
{
int * ii = i;
--i;
if (*i < *ii)
{
int * j = last;
while (!(*i < *--j)) // 由尾端往前找,直到遇上比 *i 大的元素
;
swap(*i, *j);
reverse(ii, last);
return true;
}
}
if (i == first) // 当前排列为字典序的最后一个排列
{
reverse(first, last); // 全部逆向排列,即为升序
return false;
}
}
bool prev_premutation(int * first, int * last)
{
if (first == last) return false; // 空区间
int * i = first;
++i;
if (i == last) return false; // 只有一个元素
i = last;
--i;
for (;;)
{
int * ii = i;
--i;
if (*i > *ii)
{
int * j = last;
while (!(*i > *--j)) // 由尾端往前找,直到遇上比 *i 大的元素
;
swap(*i, *j);
reverse(ii, last);
return true;
}
}
if (i == first) // 当前排列为字典序的第一个排列
{
reverse(first, last); // 全部逆向排列,即为降序
return false;
}
}
结后语
这篇文章主要介绍了解决不重复序列的全排列问题的两个方法:递归和字典序法。
转自:刘毅
https://61mon.com/index.php/archives/197/